Sliced-Wasserstein Flows: Nonparametric Generative Modeling via Optimal Transport and Diffusions
Paper and Code
Jun 21, 2018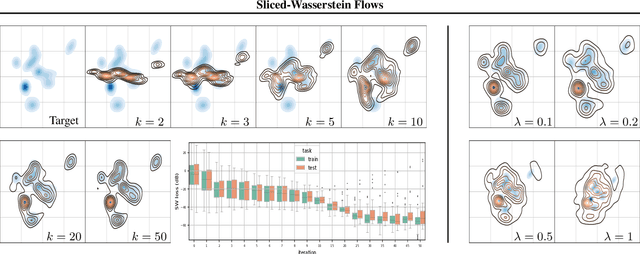
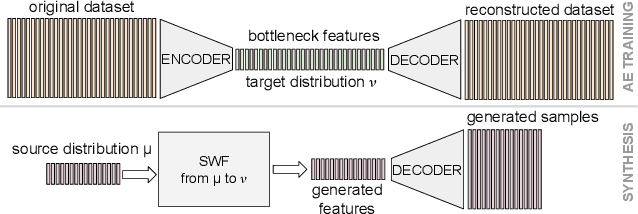


By building up on the recent theory that established the connection between implicit generative modeling and optimal transport, in this study, we propose a novel parameter-free algorithm for learning the underlying distributions of complicated datasets and sampling from them. The proposed algorithm is based on a functional optimization problem, which aims at finding a measure that is close to the data distribution as much as possible and also expressive enough for generative modeling purposes. We formulate the problem as a gradient flow in the space of probability measures. The connections between gradient flows and stochastic differential equations let us develop a computationally efficient algorithm for solving the optimization problem, where the resulting algorithm resembles the recent dynamics-based Markov Chain Monte Carlo algorithms. We provide formal theoretical analysis where we prove finite-time error guarantees for the proposed algorithm. Our experimental results support our theory and shows that our algorithm is able to capture the structure of challenging distributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge