Langevin Monte Carlo Beyond Lipschitz Gradient Continuity

We present a significant advancement in the field of Langevin Monte Carlo (LMC) methods by introducing the Inexact Proximal Langevin Algorithm (IPLA). This novel algorithm broadens the scope of problems that LMC can effectively address while maintaining controlled computational costs. IPLA extends LMC's applicability to potentials that are convex, strongly convex in the tails, and exhibit polynomial growth, beyond the conventional $L$-smoothness assumption. Moreover, we extend LMC's applicability to super-quadratic potentials and offer improved convergence rates over existing algorithms. Additionally, we provide bounds on all moments of the Markov chain generated by IPLA, enhancing its analytical robustness.

Structure learning for CTBN's via penalized maximum likelihood methods

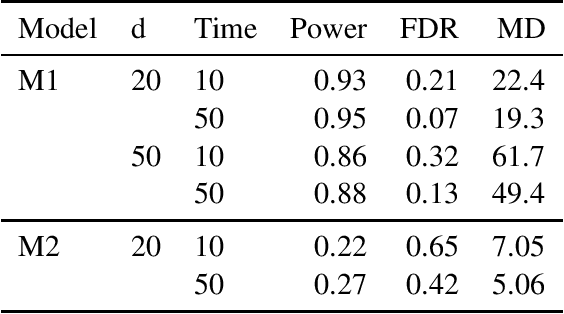
The continuous-time Bayesian networks (CTBNs) represent a class of stochastic processes, which can be used to model complex phenomena, for instance, they can describe interactions occurring in living processes, in social science models or in medicine. The literature on this topic is usually focused on the case when the dependence structure of a system is known and we are to determine conditional transition intensities (parameters of the network). In the paper, we study the structure learning problem, which is a more challenging task and the existing research on this topic is limited. The approach, which we propose, is based on a penalized likelihood method. We prove that our algorithm, under mild regularity conditions, recognizes the dependence structure of the graph with high probability. We also investigate the properties of the procedure in numerical studies to demonstrate its effectiveness.

Analysis of Langevin Monte Carlo via convex optimization

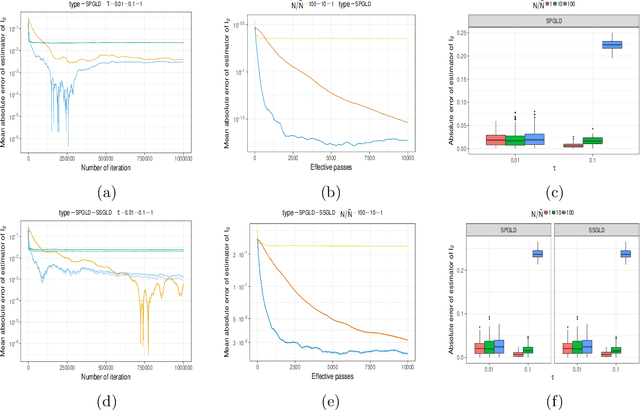
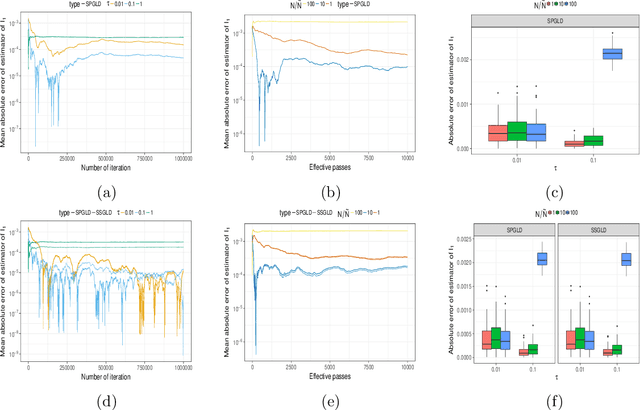
In this paper, we provide new insights on the Unadjusted Langevin Algorithm. We show that this method can be formulated as a first order optimization algorithm of an objective functional defined on the Wasserstein space of order $2$. Using this interpretation and techniques borrowed from convex optimization, we give a non-asymptotic analysis of this method to sample from logconcave smooth target distribution on $\mathbb{R}^d$. Based on this interpretation, we propose two new methods for sampling from a non-smooth target distribution, which we analyze as well. Besides, these new algorithms are natural extensions of the Stochastic Gradient Langevin Dynamics (SGLD) algorithm, which is a popular extension of the Unadjusted Langevin Algorithm. Similar to SGLD, they only rely on approximations of the gradient of the target log density and can be used for large-scale Bayesian inference.