Wojciech Rejchel
Class prior estimation for positive-unlabeled learning when label shift occurs
Feb 28, 2025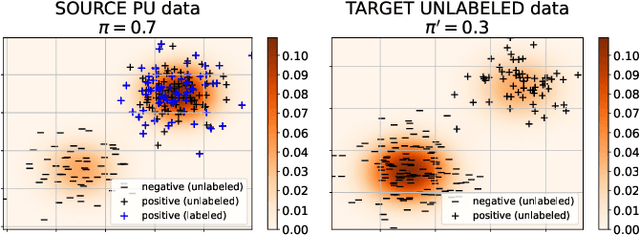
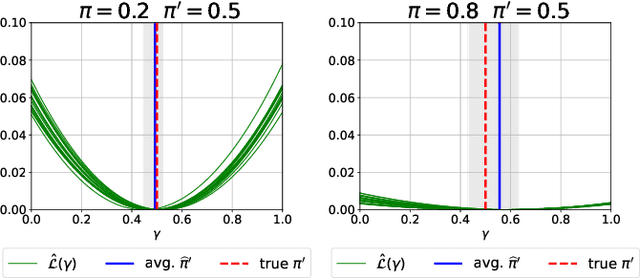
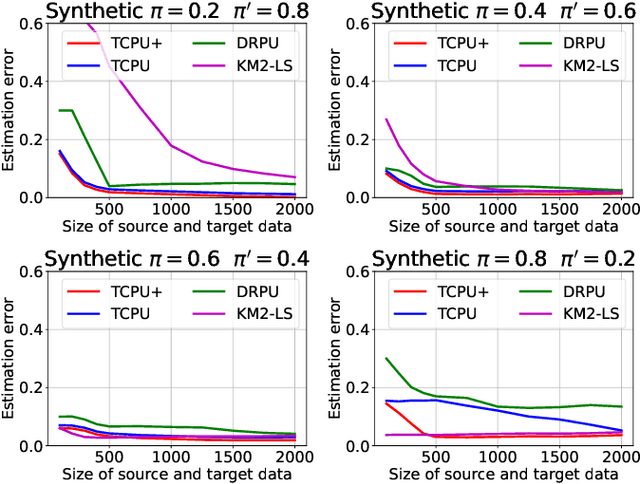
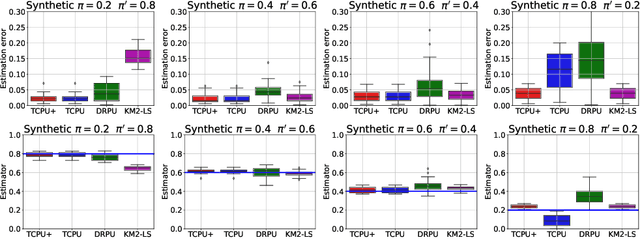
Abstract:We study estimation of class prior for unlabeled target samples which is possibly different from that of source population. It is assumed that for the source data only samples from positive class and from the whole population are available (PU learning scenario). We introduce a novel direct estimator of class prior which avoids estimation of posterior probabilities and has a simple geometric interpretation. It is based on a distribution matching technique together with kernel embedding and is obtained as an explicit solution to an optimisation task. We establish its asymptotic consistency as well as a non-asymptotic bound on its deviation from the unknown prior, which is calculable in practice. We study finite sample behaviour for synthetic and real data and show that the proposal, together with a suitably modified version for large values of source prior, works on par or better than its competitors.
Joint empirical risk minimization for instance-dependent positive-unlabeled data
Dec 27, 2023Abstract:Learning from positive and unlabeled data (PU learning) is actively researched machine learning task. The goal is to train a binary classification model based on a training dataset containing part of positives which are labeled, and unlabeled instances. Unlabeled set includes remaining part of positives and all negative observations. An important element in PU learning is modeling of the labeling mechanism, i.e. labels' assignment to positive observations. Unlike in many prior works, we consider a realistic setting for which probability of label assignment, i.e. propensity score, is instance-dependent. In our approach we investigate minimizer of an empirical counterpart of a joint risk which depends on both posterior probability of inclusion in a positive class as well as on a propensity score. The non-convex empirical risk is alternately optimised with respect to parameters of both functions. In the theoretical analysis we establish risk consistency of the minimisers using recently derived methods from the theory of empirical processes. Besides, the important development here is a proposed novel implementation of an optimisation algorithm, for which sequential approximation of a set of positive observations among unlabeled ones is crucial. This relies on modified technique of 'spies' as well as on a thresholding rule based on conditional probabilities. Experiments conducted on 20 data sets for various labeling scenarios show that the proposed method works on par or more effectively than state-of-the-art methods based on propensity function estimation.
Improving Group Lasso for high-dimensional categorical data
Oct 27, 2022Abstract:Sparse modelling or model selection with categorical data is challenging even for a moderate number of variables, because one parameter is roughly needed to encode one category or level. The Group Lasso is a well known efficient algorithm for selection continuous or categorical variables, but all estimates related to a selected factor usually differ. Therefore, a fitted model may not be sparse, which makes the model interpretation difficult. To obtain a sparse solution of the Group Lasso we propose the following two-step procedure: first, we reduce data dimensionality using the Group Lasso; then to choose the final model we use an information criterion on a small family of models prepared by clustering levels of individual factors. We investigate selection correctness of the algorithm in a sparse high-dimensional scenario. We also test our method on synthetic as well as real datasets and show that it performs better than the state of the art algorithms with respect to the prediction accuracy or model dimension.
Joint estimation of posterior probability and propensity score function for positive and unlabelled data
Sep 16, 2022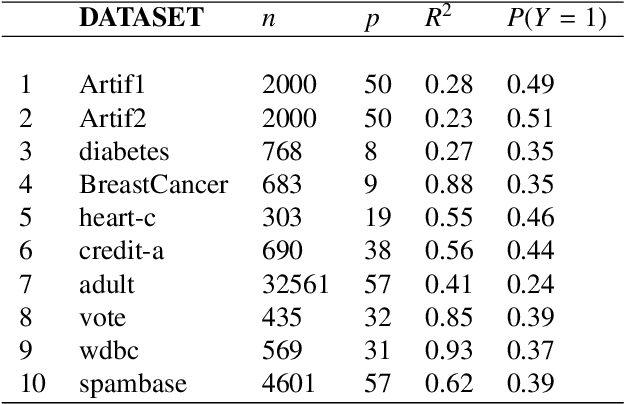
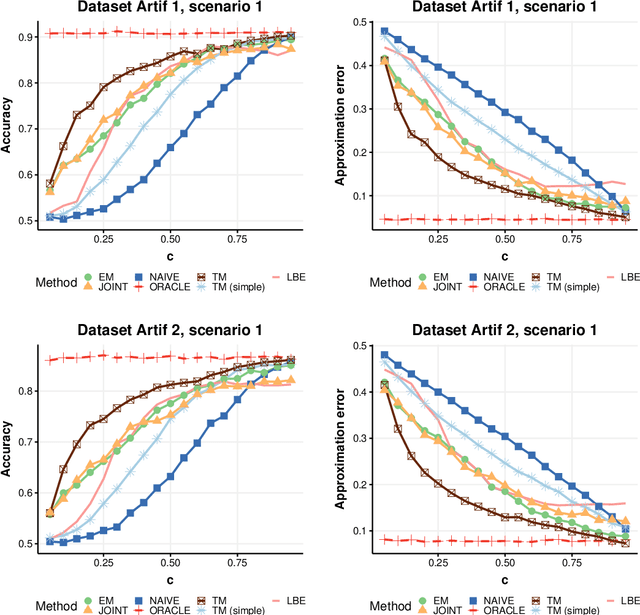
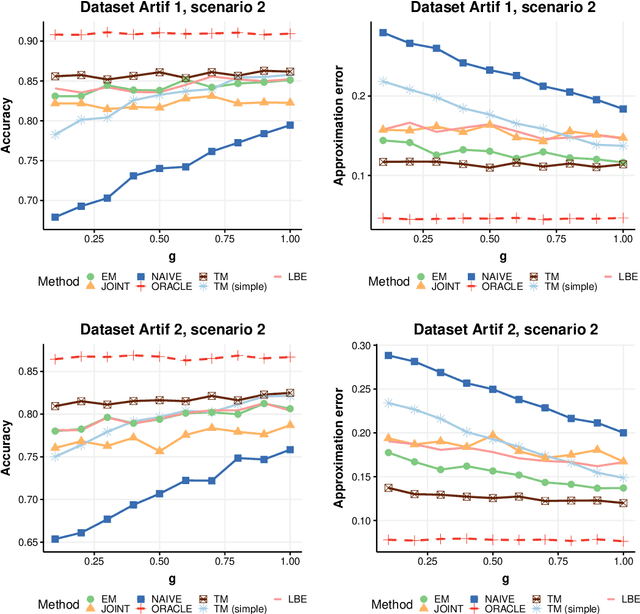
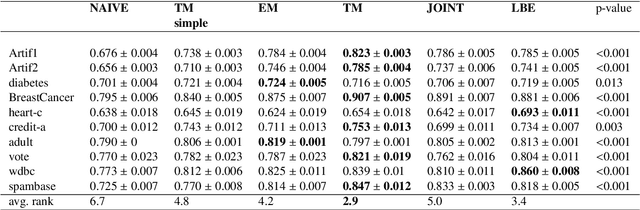
Abstract:Positive and unlabelled learning is an important problem which arises naturally in many applications. The significant limitation of almost all existing methods lies in assuming that the propensity score function is constant (SCAR assumption), which is unrealistic in many practical situations. Avoiding this assumption, we consider parametric approach to the problem of joint estimation of posterior probability and propensity score functions. We show that under mild assumptions when both functions have the same parametric form (e.g. logistic with different parameters) the corresponding parameters are identifiable. Motivated by this, we propose two approaches to their estimation: joint maximum likelihood method and the second approach based on alternating maximization of two Fisher consistent expressions. Our experimental results show that the proposed methods are comparable or better than the existing methods based on Expectation-Maximisation scheme.
Structure learning for CTBN's via penalized maximum likelihood methods
Jun 13, 2020
Abstract:The continuous-time Bayesian networks (CTBNs) represent a class of stochastic processes, which can be used to model complex phenomena, for instance, they can describe interactions occurring in living processes, in social science models or in medicine. The literature on this topic is usually focused on the case when the dependence structure of a system is known and we are to determine conditional transition intensities (parameters of the network). In the paper, we study the structure learning problem, which is a more challenging task and the existing research on this topic is limited. The approach, which we propose, is based on a penalized likelihood method. We prove that our algorithm, under mild regularity conditions, recognizes the dependence structure of the graph with high probability. We also investigate the properties of the procedure in numerical studies to demonstrate its effectiveness.
Oracle inequalities for ranking and U-processes with Lasso penalty
Dec 17, 2015Abstract:We investigate properties of estimators obtained by minimization of U-processes with the Lasso penalty in high-dimensional settings. Our attention is focused on the ranking problem that is popular in machine learning. It is related to guessing the ordering between objects on the basis of their observed predictors. We prove the oracle inequality for the excess risk of the considered estimator as well as the bound for the l1 distance between the estimator and the oracle.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge