Improving Group Lasso for high-dimensional categorical data

Sparse modelling or model selection with categorical data is challenging even for a moderate number of variables, because one parameter is roughly needed to encode one category or level. The Group Lasso is a well known efficient algorithm for selection continuous or categorical variables, but all estimates related to a selected factor usually differ. Therefore, a fitted model may not be sparse, which makes the model interpretation difficult. To obtain a sparse solution of the Group Lasso we propose the following two-step procedure: first, we reduce data dimensionality using the Group Lasso; then to choose the final model we use an information criterion on a small family of models prepared by clustering levels of individual factors. We investigate selection correctness of the algorithm in a sparse high-dimensional scenario. We also test our method on synthetic as well as real datasets and show that it performs better than the state of the art algorithms with respect to the prediction accuracy or model dimension.

Combined l_1 and greedy l_0 penalized least squares for linear model selection

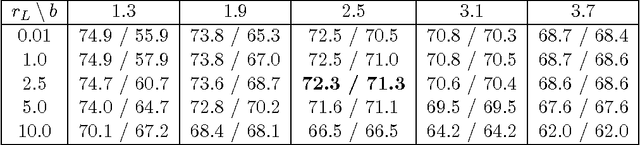
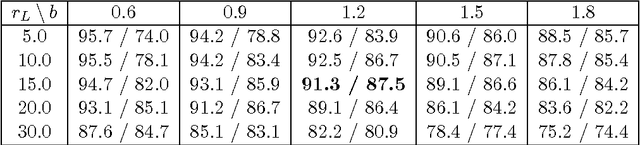
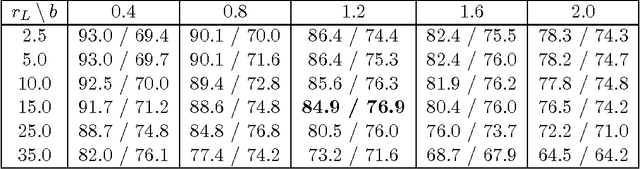
We introduce a computationally effective algorithm for a linear model selection consisting of three steps: screening--ordering--selection (SOS). Screening of predictors is based on the thresholded Lasso that is l_1 penalized least squares. The screened predictors are then fitted using least squares (LS) and ordered with respect to their t statistics. Finally, a model is selected using greedy generalized information criterion (GIC) that is l_0 penalized LS in a nested family induced by the ordering. We give non-asymptotic upper bounds on error probability of each step of the SOS algorithm in terms of both penalties. Then we obtain selection consistency for different (n, p) scenarios under conditions which are needed for screening consistency of the Lasso. For the traditional setting (n >p) we give Sanov-type bounds on the error probabilities of the ordering--selection algorithm. Its surprising consequence is that the selection error of greedy GIC is asymptotically not larger than of exhaustive GIC. We also obtain new bounds on prediction and estimation errors for the Lasso which are proved in parallel for the algorithm used in practice and its formal version.