Combined l_1 and greedy l_0 penalized least squares for linear model selection
Paper and Code
Oct 22, 2013
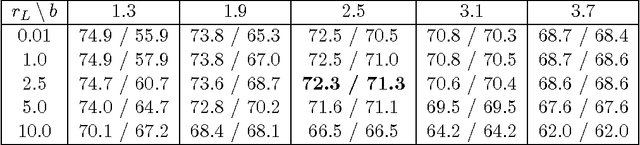
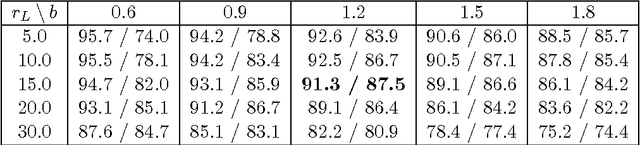
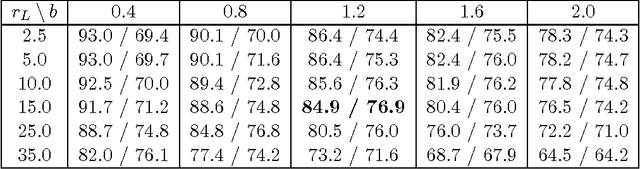
We introduce a computationally effective algorithm for a linear model selection consisting of three steps: screening--ordering--selection (SOS). Screening of predictors is based on the thresholded Lasso that is l_1 penalized least squares. The screened predictors are then fitted using least squares (LS) and ordered with respect to their t statistics. Finally, a model is selected using greedy generalized information criterion (GIC) that is l_0 penalized LS in a nested family induced by the ordering. We give non-asymptotic upper bounds on error probability of each step of the SOS algorithm in terms of both penalties. Then we obtain selection consistency for different (n, p) scenarios under conditions which are needed for screening consistency of the Lasso. For the traditional setting (n >p) we give Sanov-type bounds on the error probabilities of the ordering--selection algorithm. Its surprising consequence is that the selection error of greedy GIC is asymptotically not larger than of exhaustive GIC. We also obtain new bounds on prediction and estimation errors for the Lasso which are proved in parallel for the algorithm used in practice and its formal version.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge