Jan Mielniczuk
A generalized approach to label shift: the Conditional Probability Shift Model
Mar 04, 2025Abstract:In many practical applications of machine learning, a discrepancy often arises between a source distribution from which labeled training examples are drawn and a target distribution for which only unlabeled data is observed. Traditionally, two main scenarios have been considered to address this issue: covariate shift (CS), where only the marginal distribution of features changes, and label shift (LS), which involves a change in the class variable's prior distribution. However, these frameworks do not encompass all forms of distributional shift. This paper introduces a new setting, Conditional Probability Shift (CPS), which captures the case when the conditional distribution of the class variable given some specific features changes while the distribution of remaining features given the specific features and the class is preserved. For this scenario we present the Conditional Probability Shift Model (CPSM) based on modeling the class variable's conditional probabilities using multinomial regression. Since the class variable is not observed for the target data, the parameters of the multinomial model for its distribution are estimated using the Expectation-Maximization algorithm. The proposed method is generic and can be combined with any probabilistic classifier. The effectiveness of CPSM is demonstrated through experiments on synthetic datasets and a case study using the MIMIC medical database, revealing its superior balanced classification accuracy on the target data compared to existing methods, particularly in situations situations of conditional distribution shift and no apriori distribution shift, which are not detected by LS-based methods.
Class prior estimation for positive-unlabeled learning when label shift occurs
Feb 28, 2025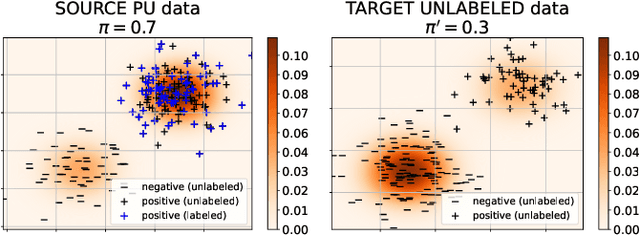
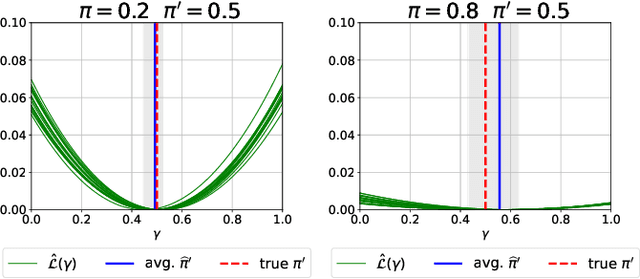
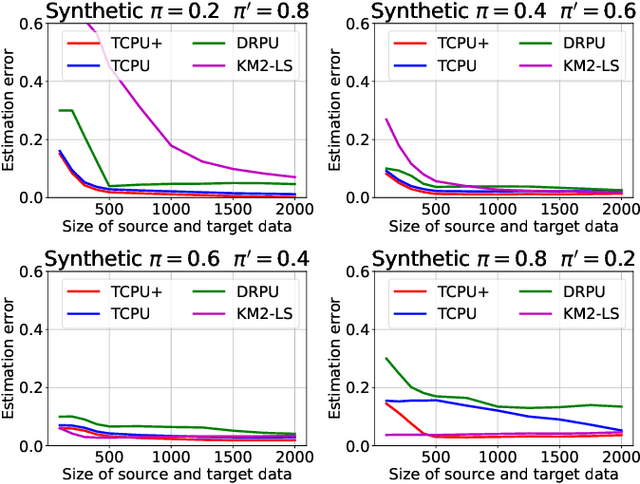
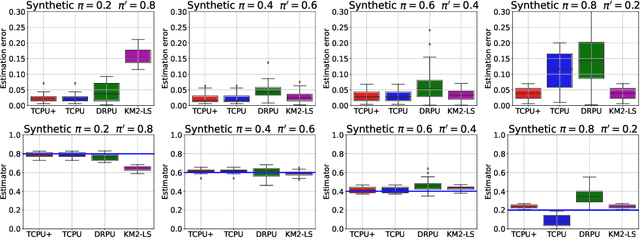
Abstract:We study estimation of class prior for unlabeled target samples which is possibly different from that of source population. It is assumed that for the source data only samples from positive class and from the whole population are available (PU learning scenario). We introduce a novel direct estimator of class prior which avoids estimation of posterior probabilities and has a simple geometric interpretation. It is based on a distribution matching technique together with kernel embedding and is obtained as an explicit solution to an optimisation task. We establish its asymptotic consistency as well as a non-asymptotic bound on its deviation from the unknown prior, which is calculable in practice. We study finite sample behaviour for synthetic and real data and show that the proposal, together with a suitably modified version for large values of source prior, works on par or better than its competitors.
Augmented prediction of a true class for Positive Unlabeled data under selection bias
Jul 14, 2024Abstract:We introduce a new observational setting for Positive Unlabeled (PU) data where the observations at prediction time are also labeled. This occurs commonly in practice -- we argue that the additional information is important for prediction, and call this task "augmented PU prediction". We allow for labeling to be feature dependent. In such scenario, Bayes classifier and its risk is established and compared with a risk of a classifier which for unlabeled data is based only on predictors. We introduce several variants of the empirical Bayes rule in such scenario and investigate their performance. We emphasise dangers (and ease) of applying classical classification rule in the augmented PU scenario -- due to no preexisting studies, an unaware researcher is prone to skewing the obtained predictions. We conclude that the variant based on recently proposed variational autoencoder designed for PU scenario works on par or better than other considered variants and yields advantage over feature-only based methods in terms of accuracy for unlabeled samples.
Verifying the Selected Completely at Random Assumption in Positive-Unlabeled Learning
Mar 29, 2024Abstract:The goal of positive-unlabeled (PU) learning is to train a binary classifier on the basis of training data containing positive and unlabeled instances, where unlabeled observations can belong either to the positive class or to the negative class. Modeling PU data requires certain assumptions on the labeling mechanism that describes which positive observations are assigned a label. The simplest assumption, considered in early works, is SCAR (Selected Completely at Random Assumption), according to which the propensity score function, defined as the probability of assigning a label to a positive observation, is constant. On the other hand, a much more realistic assumption is SAR (Selected at Random), which states that the propensity function solely depends on the observed feature vector. SCAR-based algorithms are much simpler and computationally much faster compared to SAR-based algorithms, which usually require challenging estimation of the propensity score. In this work, we propose a relatively simple and computationally fast test that can be used to determine whether the observed data meet the SCAR assumption. Our test is based on generating artificial labels conforming to the SCAR case, which in turn allows to mimic the distribution of the test statistic under the null hypothesis of SCAR. We justify our method theoretically. In experiments, we demonstrate that the test successfully detects various deviations from SCAR scenario and at the same time it is possible to effectively control the type I error. The proposed test can be recommended as a pre-processing step to decide which final PU algorithm to choose in cases when nature of labeling mechanism is not known.
Joint empirical risk minimization for instance-dependent positive-unlabeled data
Dec 27, 2023Abstract:Learning from positive and unlabeled data (PU learning) is actively researched machine learning task. The goal is to train a binary classification model based on a training dataset containing part of positives which are labeled, and unlabeled instances. Unlabeled set includes remaining part of positives and all negative observations. An important element in PU learning is modeling of the labeling mechanism, i.e. labels' assignment to positive observations. Unlike in many prior works, we consider a realistic setting for which probability of label assignment, i.e. propensity score, is instance-dependent. In our approach we investigate minimizer of an empirical counterpart of a joint risk which depends on both posterior probability of inclusion in a positive class as well as on a propensity score. The non-convex empirical risk is alternately optimised with respect to parameters of both functions. In the theoretical analysis we establish risk consistency of the minimisers using recently derived methods from the theory of empirical processes. Besides, the important development here is a proposed novel implementation of an optimisation algorithm, for which sequential approximation of a set of positive observations among unlabeled ones is crucial. This relies on modified technique of 'spies' as well as on a thresholding rule based on conditional probabilities. Experiments conducted on 20 data sets for various labeling scenarios show that the proposed method works on par or more effectively than state-of-the-art methods based on propensity function estimation.
Single-sample versus case-control sampling scheme for Positive Unlabeled data: the story of two scenarios
Dec 04, 2023Abstract:In the paper we argue that performance of the classifiers based on Empirical Risk Minimization (ERM) for positive unlabeled data, which are designed for case-control sampling scheme may significantly deteriorate when applied to a single-sample scenario. We reveal why their behavior depends, in all but very specific cases, on the scenario. Also, we introduce a single-sample case analogue of the popular non-negative risk classifier designed for case-control data and compare its performance with the original proposal. We show that the significant differences occur between them, especiall when half or more positive of observations are labeled. The opposite case when ERM minimizer designed for the case-control case is applied for single-sample data is also considered and similar conclusions are drawn. Taking into account difference of scenarios requires a sole, but crucial, change in the definition of the Empirical Risk.
Enhancing naive classifier for positive unlabeled data based on logistic regression approach
Jun 05, 2023Abstract:We argue that for analysis of Positive Unlabeled (PU) data under Selected Completely At Random (SCAR) assumption it is fruitful to view the problem as fitting of misspecified model to the data. Namely, we show that the results on misspecified fit imply that in the case when posterior probability of the response is modelled by logistic regression, fitting the logistic regression to the observable PU data which {\it does not} follow this model, still yields the vector of estimated parameters approximately colinear with the true vector of parameters. This observation together with choosing the intercept of the classifier based on optimisation of analogue of F1 measure yields a classifier which performs on par or better than its competitors on several real data sets considered.
Joint estimation of posterior probability and propensity score function for positive and unlabelled data
Sep 16, 2022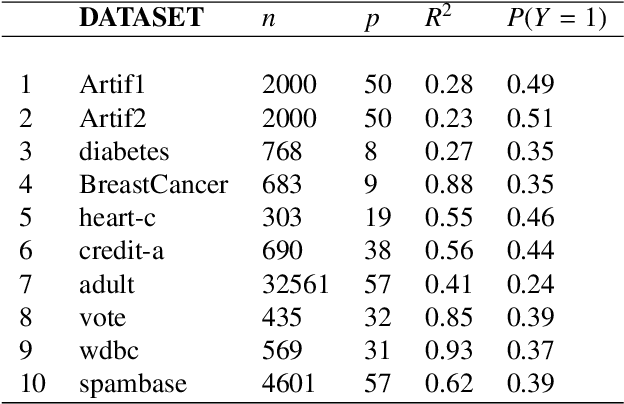
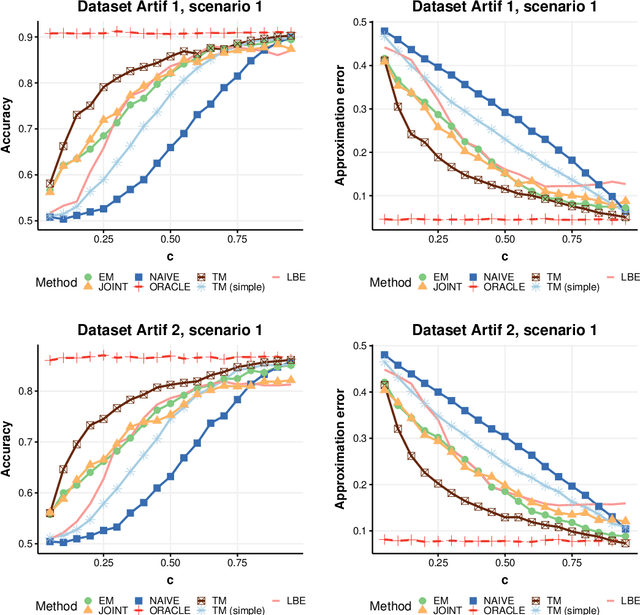
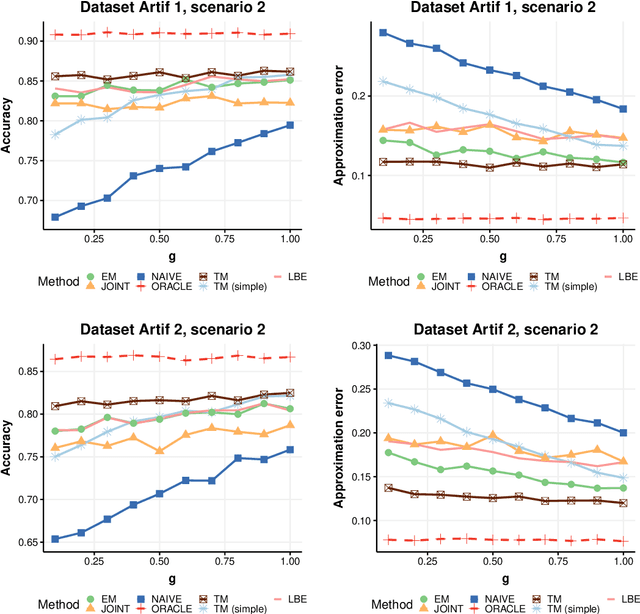
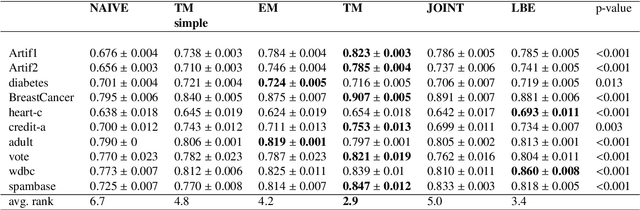
Abstract:Positive and unlabelled learning is an important problem which arises naturally in many applications. The significant limitation of almost all existing methods lies in assuming that the propensity score function is constant (SCAR assumption), which is unrealistic in many practical situations. Avoiding this assumption, we consider parametric approach to the problem of joint estimation of posterior probability and propensity score functions. We show that under mild assumptions when both functions have the same parametric form (e.g. logistic with different parameters) the corresponding parameters are identifiable. Motivated by this, we propose two approaches to their estimation: joint maximum likelihood method and the second approach based on alternating maximization of two Fisher consistent expressions. Our experimental results show that the proposed methods are comparable or better than the existing methods based on Expectation-Maximisation scheme.
Selection consistency of Lasso-based procedures for misspecified high-dimensional binary model and random regressors
Jun 10, 2019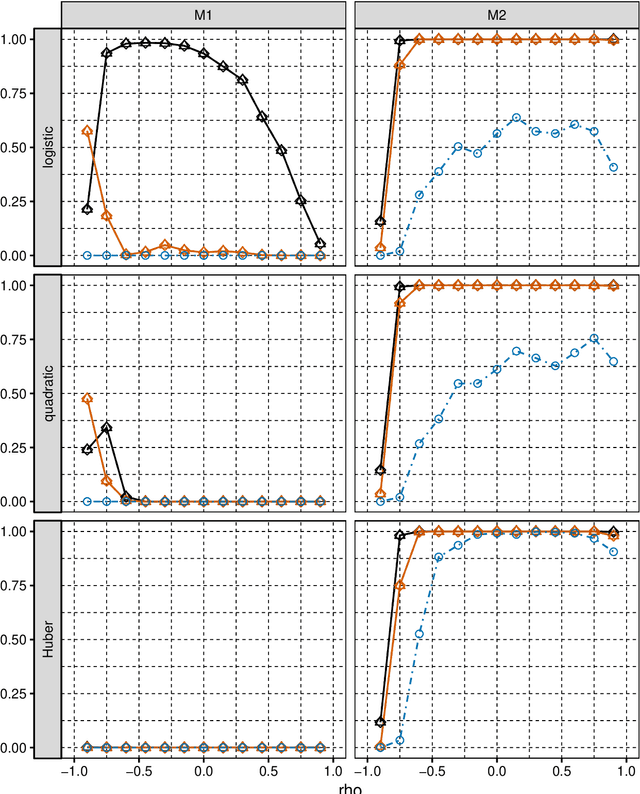
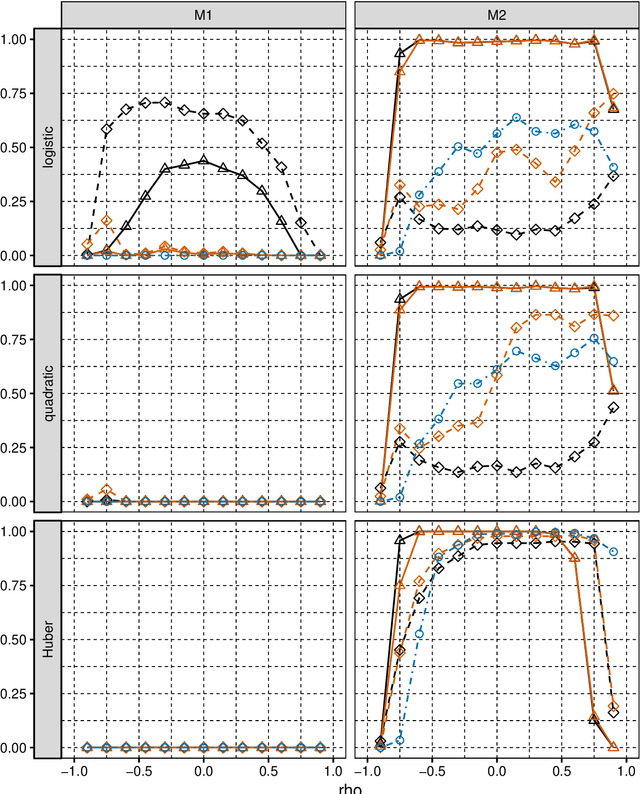
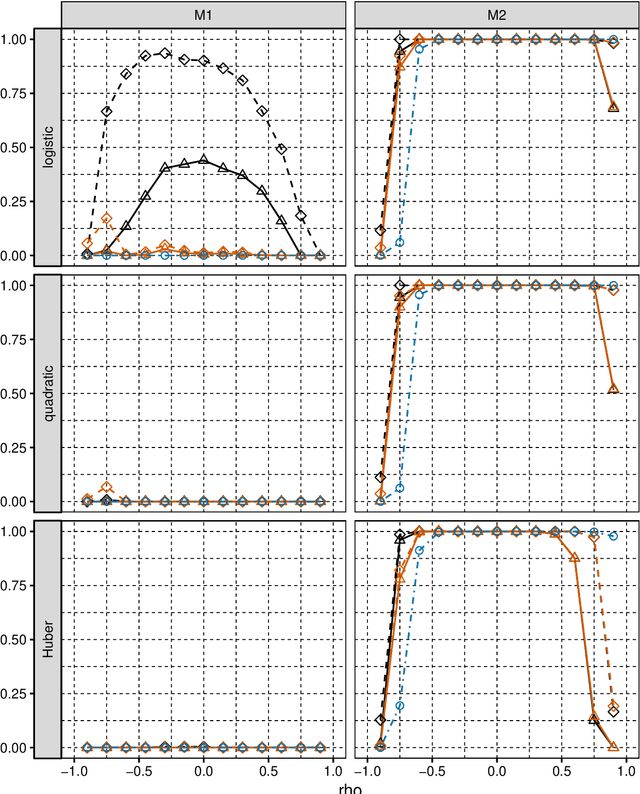
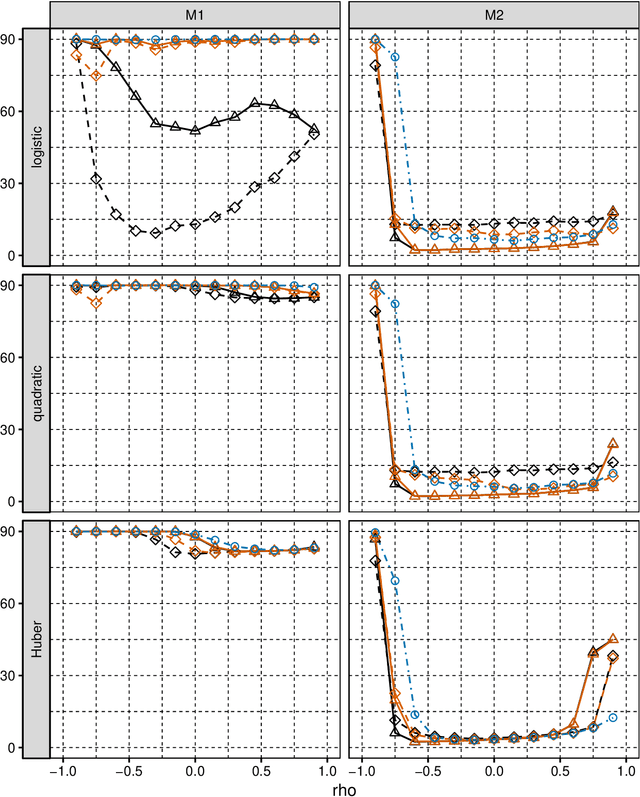
Abstract:We consider selection of random predictors for high-dimensional regression problem with binary response for a general loss function. Important special case is when the binary model is semiparametric and the response function is misspecified under parametric model fit. Selection for such a scenario aims at recovering the support of the minimizer of the associated risk with large probability. We propose a two-step selection procedure which consists of screening and ordering predictors by Lasso method and then selecting a subset of predictors which minimizes Generalized Information Criterion on the corresponding nested family of models. We prove consistency of the selection method under conditions which allow for much larger number of predictors than number of observations. For the semiparametric case when distribution of random predictors satisfies linear regression conditions the true and the estimated parameters are collinear and their common support can be consistently identified.
Combined l_1 and greedy l_0 penalized least squares for linear model selection
Oct 22, 2013
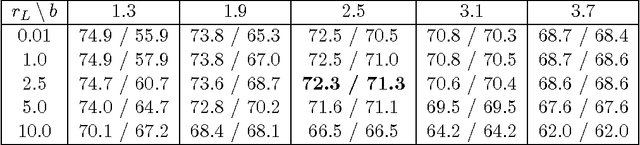
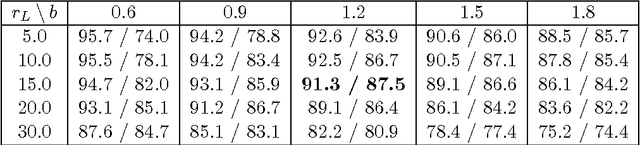
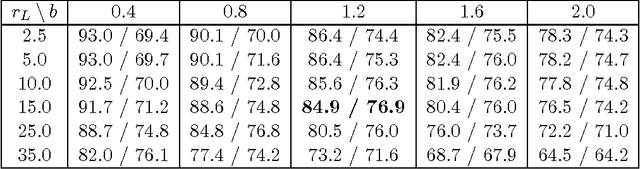
Abstract:We introduce a computationally effective algorithm for a linear model selection consisting of three steps: screening--ordering--selection (SOS). Screening of predictors is based on the thresholded Lasso that is l_1 penalized least squares. The screened predictors are then fitted using least squares (LS) and ordered with respect to their t statistics. Finally, a model is selected using greedy generalized information criterion (GIC) that is l_0 penalized LS in a nested family induced by the ordering. We give non-asymptotic upper bounds on error probability of each step of the SOS algorithm in terms of both penalties. Then we obtain selection consistency for different (n, p) scenarios under conditions which are needed for screening consistency of the Lasso. For the traditional setting (n >p) we give Sanov-type bounds on the error probabilities of the ordering--selection algorithm. Its surprising consequence is that the selection error of greedy GIC is asymptotically not larger than of exhaustive GIC. We also obtain new bounds on prediction and estimation errors for the Lasso which are proved in parallel for the algorithm used in practice and its formal version.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge