Verifying the Selected Completely at Random Assumption in Positive-Unlabeled Learning

The goal of positive-unlabeled (PU) learning is to train a binary classifier on the basis of training data containing positive and unlabeled instances, where unlabeled observations can belong either to the positive class or to the negative class. Modeling PU data requires certain assumptions on the labeling mechanism that describes which positive observations are assigned a label. The simplest assumption, considered in early works, is SCAR (Selected Completely at Random Assumption), according to which the propensity score function, defined as the probability of assigning a label to a positive observation, is constant. On the other hand, a much more realistic assumption is SAR (Selected at Random), which states that the propensity function solely depends on the observed feature vector. SCAR-based algorithms are much simpler and computationally much faster compared to SAR-based algorithms, which usually require challenging estimation of the propensity score. In this work, we propose a relatively simple and computationally fast test that can be used to determine whether the observed data meet the SCAR assumption. Our test is based on generating artificial labels conforming to the SCAR case, which in turn allows to mimic the distribution of the test statistic under the null hypothesis of SCAR. We justify our method theoretically. In experiments, we demonstrate that the test successfully detects various deviations from SCAR scenario and at the same time it is possible to effectively control the type I error. The proposed test can be recommended as a pre-processing step to decide which final PU algorithm to choose in cases when nature of labeling mechanism is not known.

Joint estimation of posterior probability and propensity score function for positive and unlabelled data

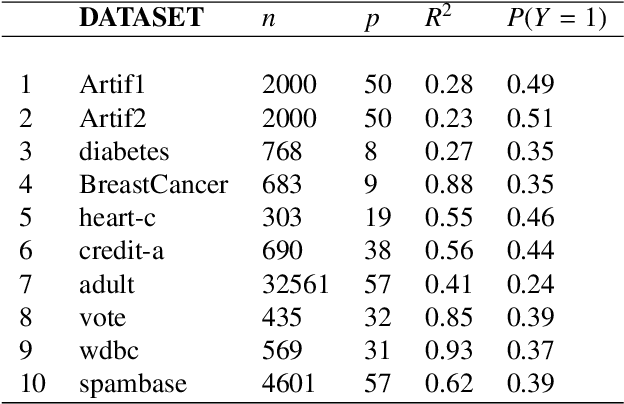
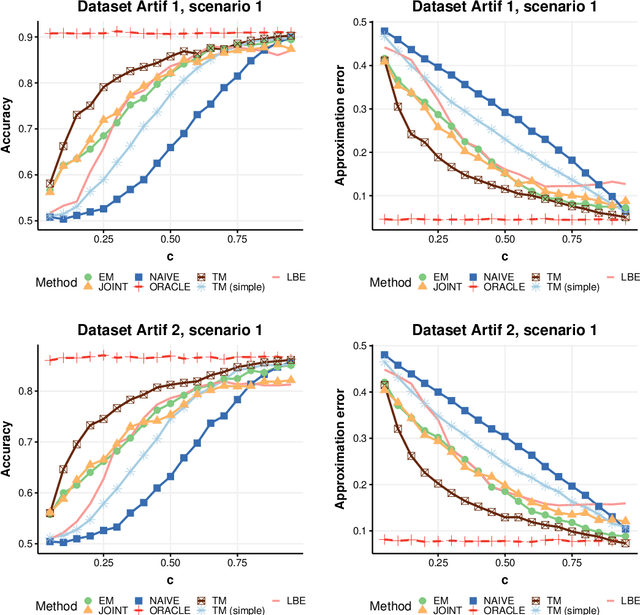
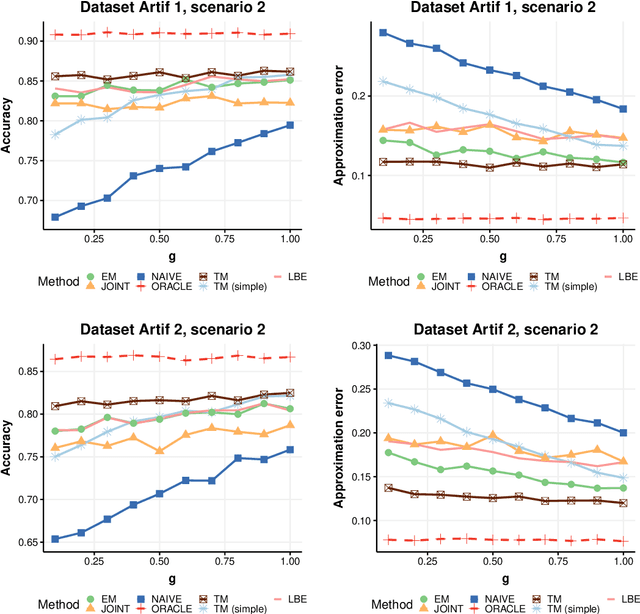
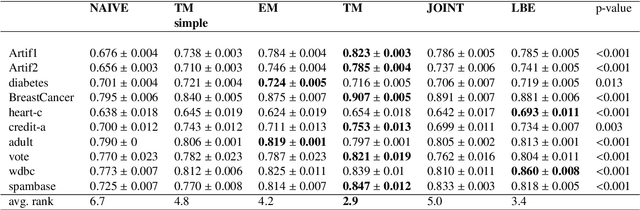
Positive and unlabelled learning is an important problem which arises naturally in many applications. The significant limitation of almost all existing methods lies in assuming that the propensity score function is constant (SCAR assumption), which is unrealistic in many practical situations. Avoiding this assumption, we consider parametric approach to the problem of joint estimation of posterior probability and propensity score functions. We show that under mild assumptions when both functions have the same parametric form (e.g. logistic with different parameters) the corresponding parameters are identifiable. Motivated by this, we propose two approaches to their estimation: joint maximum likelihood method and the second approach based on alternating maximization of two Fisher consistent expressions. Our experimental results show that the proposed methods are comparable or better than the existing methods based on Expectation-Maximisation scheme.