Selection consistency of Lasso-based procedures for misspecified high-dimensional binary model and random regressors
Paper and Code
Jun 10, 2019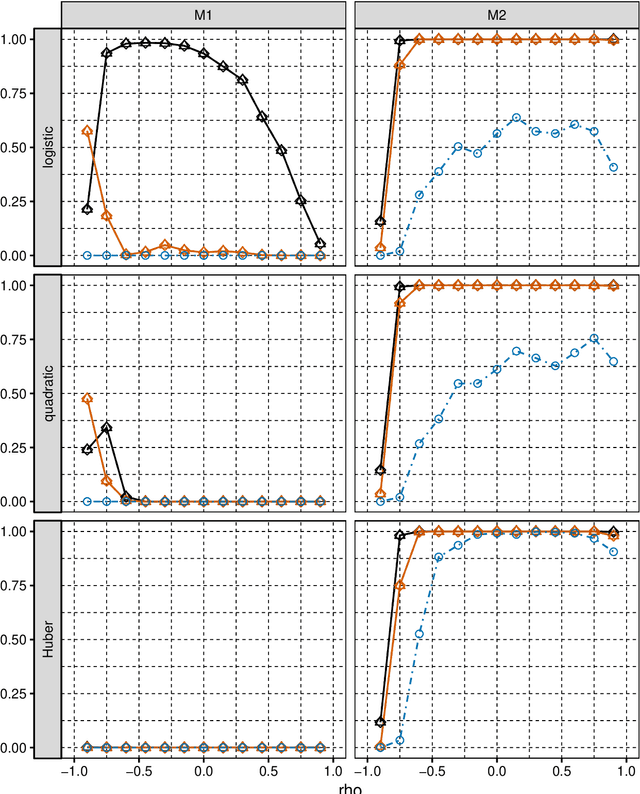
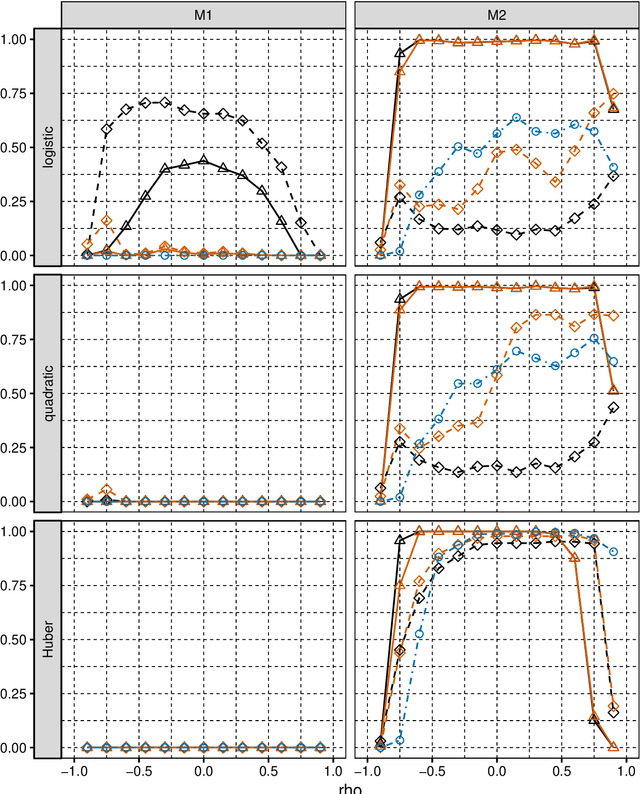
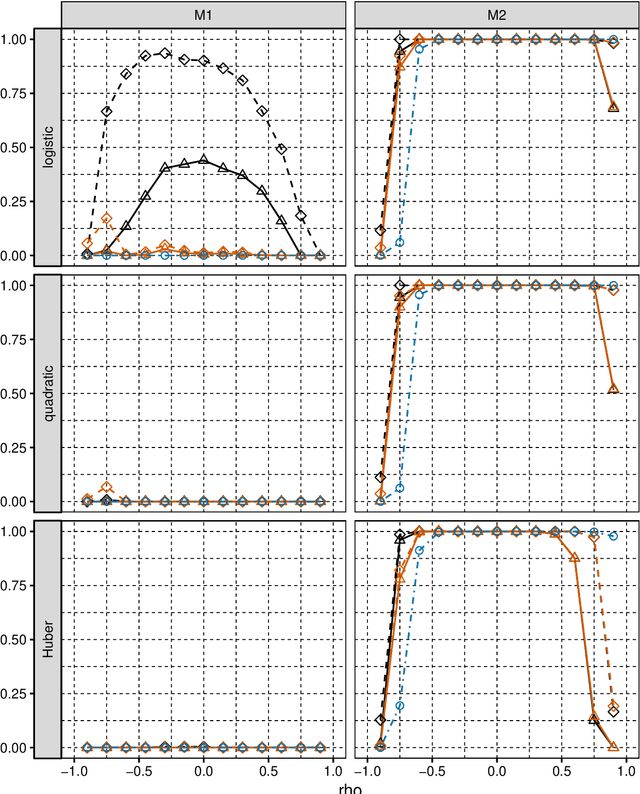
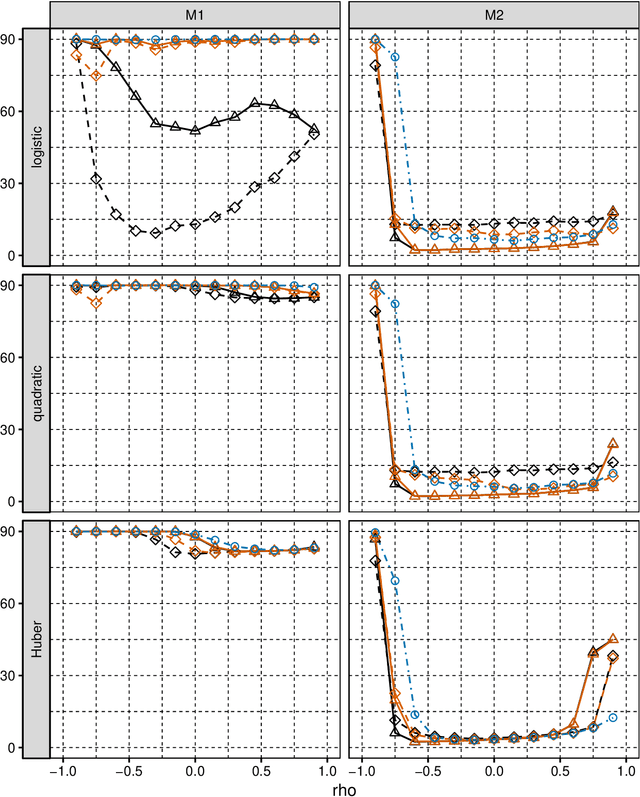
We consider selection of random predictors for high-dimensional regression problem with binary response for a general loss function. Important special case is when the binary model is semiparametric and the response function is misspecified under parametric model fit. Selection for such a scenario aims at recovering the support of the minimizer of the associated risk with large probability. We propose a two-step selection procedure which consists of screening and ordering predictors by Lasso method and then selecting a subset of predictors which minimizes Generalized Information Criterion on the corresponding nested family of models. We prove consistency of the selection method under conditions which allow for much larger number of predictors than number of observations. For the semiparametric case when distribution of random predictors satisfies linear regression conditions the true and the estimated parameters are collinear and their common support can be consistently identified.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge