Analyzing Credit Risk Model Problems through NLP-Based Clustering and Machine Learning: Insights from Validation Reports

This paper explores the use of clustering methods and machine learning algorithms, including Natural Language Processing (NLP), to identify and classify problems identified in credit risk models through textual information contained in validation reports. Using a unique dataset of 657 findings raised by validation teams in a large international banking group between January 2019 and December 2022. The findings are classified into nine validation dimensions and assigned a severity level by validators using their expert knowledge. The authors use embedding generation for the findings' titles and observations using four different pre-trained models, including "module\_url" from TensorFlow Hub and three models from the SentenceTransformer library, namely "all-mpnet-base-v2", "all-MiniLM-L6-v2", and "paraphrase-mpnet-base-v2". The paper uses and compares various clustering methods in grouping findings with similar characteristics, enabling the identification of common problems within each validation dimension and severity. The results of the study show that clustering is an effective approach for identifying and classifying credit risk model problems with accuracy higher than 60\%. The authors also employ machine learning algorithms, including logistic regression and XGBoost, to predict the validation dimension and its severity, achieving an accuracy of 80\% for XGBoost algorithm. Furthermore, the study identifies the top 10 words that predict a validation dimension and severity. Overall, this paper makes a contribution by demonstrating the usefulness of clustering and machine learning for analyzing textual information in validation reports, and providing insights into the types of problems encountered in the development and validation of credit risk models.

Selection consistency of Lasso-based procedures for misspecified high-dimensional binary model and random regressors

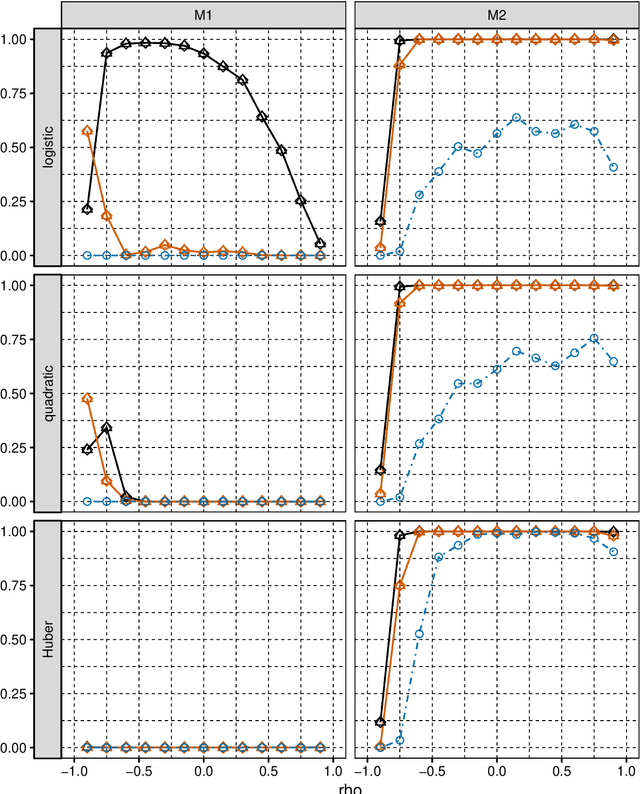
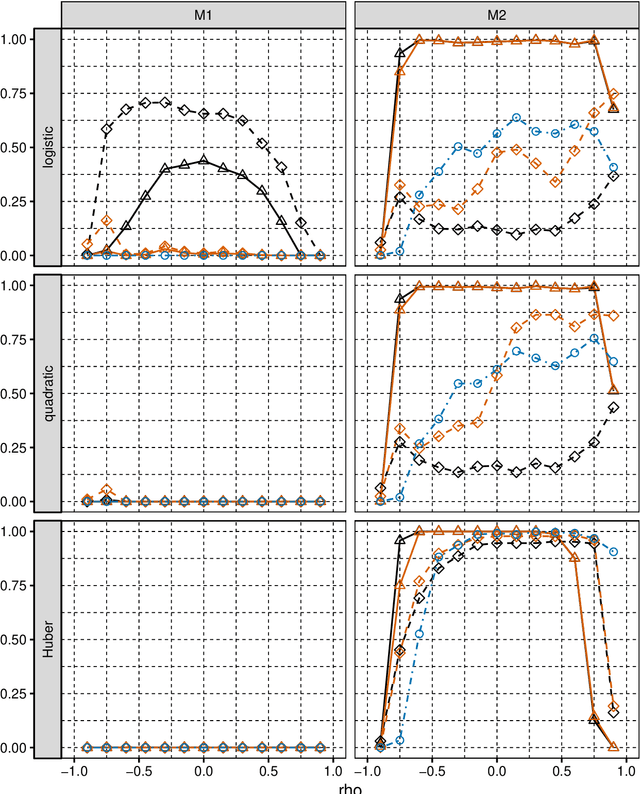
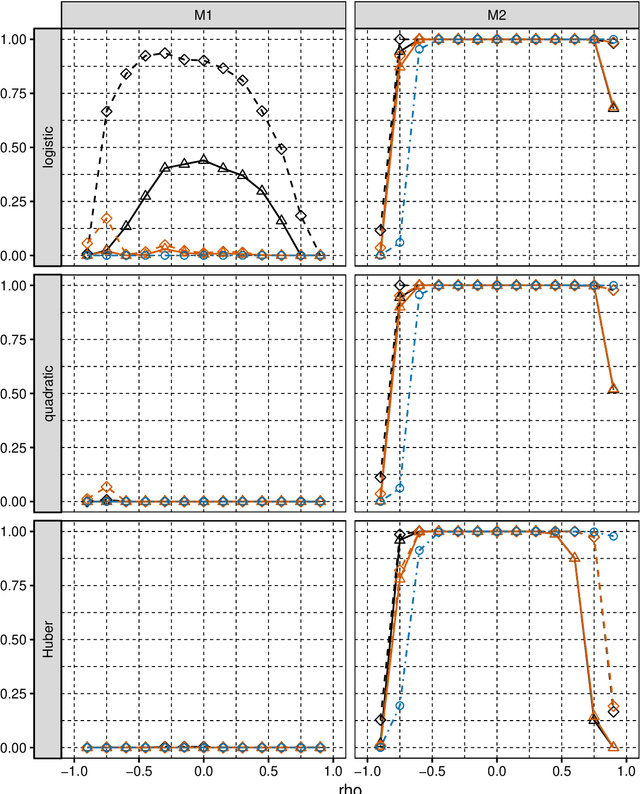
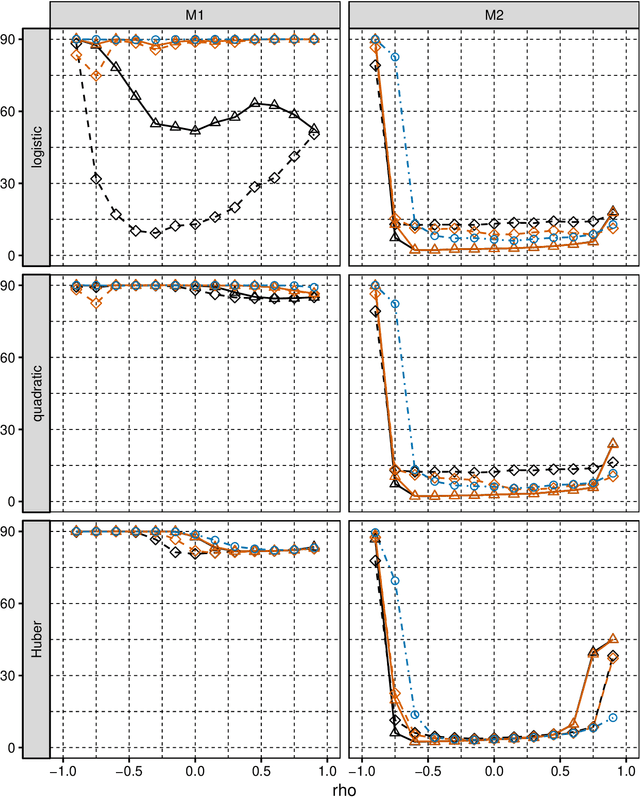
We consider selection of random predictors for high-dimensional regression problem with binary response for a general loss function. Important special case is when the binary model is semiparametric and the response function is misspecified under parametric model fit. Selection for such a scenario aims at recovering the support of the minimizer of the associated risk with large probability. We propose a two-step selection procedure which consists of screening and ordering predictors by Lasso method and then selecting a subset of predictors which minimizes Generalized Information Criterion on the corresponding nested family of models. We prove consistency of the selection method under conditions which allow for much larger number of predictors than number of observations. For the semiparametric case when distribution of random predictors satisfies linear regression conditions the true and the estimated parameters are collinear and their common support can be consistently identified.