Structure Learning and Parameter Estimation for Graphical Models via Penalized Maximum Likelihood Methods

Probabilistic graphical models (PGMs) provide a compact and flexible framework to model very complex real-life phenomena. They combine the probability theory which deals with uncertainty and logical structure represented by a graph which allows one to cope with the computational complexity and also interpret and communicate the obtained knowledge. In the thesis, we consider two different types of PGMs: Bayesian networks (BNs) which are static, and continuous time Bayesian networks which, as the name suggests, have a temporal component. We are interested in recovering their true structure, which is the first step in learning any PGM. This is a challenging task, which is interesting in itself from the causal point of view, for the purposes of interpretation of the model and the decision-making process. All approaches for structure learning in the thesis are united by the same idea of maximum likelihood estimation with the LASSO penalty. The problem of structure learning is reduced to the problem of finding non-zero coefficients in the LASSO estimator for a generalized linear model. In the case of CTBNs, we consider the problem both for complete and incomplete data. We support the theoretical results with experiments.

Structure learning for CTBN's via penalized maximum likelihood methods

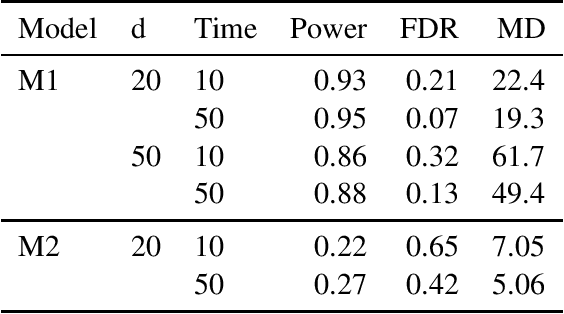
The continuous-time Bayesian networks (CTBNs) represent a class of stochastic processes, which can be used to model complex phenomena, for instance, they can describe interactions occurring in living processes, in social science models or in medicine. The literature on this topic is usually focused on the case when the dependence structure of a system is known and we are to determine conditional transition intensities (parameters of the network). In the paper, we study the structure learning problem, which is a more challenging task and the existing research on this topic is limited. The approach, which we propose, is based on a penalized likelihood method. We prove that our algorithm, under mild regularity conditions, recognizes the dependence structure of the graph with high probability. We also investigate the properties of the procedure in numerical studies to demonstrate its effectiveness.