Multi-agent Coverage Control: From Discrete Assignments to Continuous Multi-agent Distribution Matching

The multi-agent spatial coverage control problem encompasses a broad research domain, dealing with both dynamic and static deployment strategies, discrete-task assignments, and spatial distribution-matching deployment. Coverage control may involve the deployment of a finite number of agents or a continuum through centralized or decentralized, locally-interacting schemes. All these problems can be solved via a different taxonomy of deployment algorithms for multiple agents. Depending on the application scenario, these problems involve from purely discrete descriptions of tasks (finite loads) and agents (finite resources), to a mixture of discrete and continuous elements, to fully continuous descriptions of the same. Yet, it is possible to find common features that underline all the above formulations, which we aim to illustrate here. By doing so, we aim to point the reader to novel references related to these problems. The short article outline is the following: Static coverage via concurrent area partitioning and assignment; Static coverage as a discrete task assignment; and Continuum task assignment for large-scale swarms.

Robotic Exploration using Generalized Behavioral Entropy

This work presents and evaluates a novel strategy for robotic exploration that leverages human models of uncertainty perception. To do this, we introduce a measure of uncertainty that we term ``Behavioral entropy'', which builds on Prelec's probability weighting from Behavioral Economics. We show that the new operator is an admissible generalized entropy, analyze its theoretical properties and compare it with other common formulations such as Shannon's and Renyi's. In particular, we discuss how the new formulation is more expressive in the sense of measures of sensitivity and perceptiveness to uncertainty introduced here. Then we use Behavioral entropy to define a new type of utility function that can guide a frontier-based environment exploration process. The approach's benefits are illustrated and compared in a Proof-of-Concept and ROS-unity simulation environment with a Clearpath Warthog robot. We show that the robot equipped with Behavioral entropy explores faster than Shannon and Renyi entropies.

Distributed Bayesian Estimation in Sensor Networks: Consensus on Marginal Densities

In this paper, we aim to design and analyze distributed Bayesian estimation algorithms for sensor networks. The challenges we address are to (i) derive a distributed provably-correct algorithm in the functional space of probability distributions over continuous variables, and (ii) leverage these results to obtain new distributed estimators restricted to subsets of variables observed by individual agents. This relates to applications such as cooperative localization and federated learning, where the data collected at any agent depends on a subset of all variables of interest. We present Bayesian density estimation algorithms using data from non-linear likelihoods at agents in centralized, distributed, and marginal distributed settings. After setting up a distributed estimation objective, we prove almost-sure convergence to the optimal set of pdfs at each agent. Then, we prove the same for a storage-aware algorithm estimating densities only over relevant variables at each agent. Finally, we present a Gaussian version of these algorithms and implement it in a mapping problem using variational inference to handle non-linear likelihood models associated with LiDAR sensing.

Distributed Variational Inference for Online Supervised Learning

Developing efficient solutions for inference problems in intelligent sensor networks is crucial for the next generation of location, tracking, and mapping services. This paper develops a scalable distributed probabilistic inference algorithm that applies to continuous variables, intractable posteriors and large-scale real-time data in sensor networks. In a centralized setting, variational inference is a fundamental technique for performing approximate Bayesian estimation, in which an intractable posterior density is approximated with a parametric density. Our key contribution lies in the derivation of a separable lower bound on the centralized estimation objective, which enables distributed variational inference with one-hop communication in a sensor network. Our distributed evidence lower bound (DELBO) consists of a weighted sum of observation likelihood and divergence to prior densities, and its gap to the measurement evidence is due to consensus and modeling errors. To solve binary classification and regression problems while handling streaming data, we design an online distributed algorithm that maximizes DELBO, and specialize it to Gaussian variational densities with non-linear likelihoods. The resulting distributed Gaussian variational inference (DGVI) efficiently inverts a $1$-rank correction to the covariance matrix. Finally, we derive a diagonalized version for online distributed inference in high-dimensional models, and apply it to multi-robot probabilistic mapping using indoor LiDAR data.

Robot Navigation in Risky, Crowded Environments: Understanding Human Preferences

Risky and crowded environments (RCE) contain abstract sources of risk and uncertainty, which are perceived differently by humans, leading to a variety of behaviors. Thus, robots deployed in RCEs, need to exhibit diverse perception and planning capabilities in order to interpret other human agents' behavior and act accordingly in such environments. To understand this problem domain, we conducted a study to explore human path choices in RCEs, enabling better robotic navigational explainable AI (XAI) designs. We created a novel COVID-19 pandemic grocery shopping scenario which had time-risk tradeoffs, and acquired users' path preferences. We found that participants showcase a variety of path preferences: from risky and urgent to safe and relaxed. To model users' decision making, we evaluated three popular risk models (Cumulative Prospect Theory (CPT), Conditional Value at Risk (CVAR), and Expected Risk (ER). We found that CPT captured people's decision making more accurately than CVaR and ER, corroborating theoretical results that CPT is more expressive and inclusive than CVaR and ER. We also found that people's self assessments of risk and time-urgency do not correlate with their path preferences in RCEs. Finally, we conducted thematic analysis of open-ended questions, providing crucial design insights for robots is RCE. Thus, through this study, we provide novel and critical insights about human behavior and perception to help design better navigational explainable AI (XAI) in RCEs.

Convex Approximation for Probabilistic Reachable Set under Data-driven Uncertainties

This paper is proposed to efficiently provide a convex approximation for the probabilistic reachable set of a dynamic system in the face of uncertainties. When the uncertainties are not limited to bounded ones, it may be impossible to find a bounded reachable set of the system. Instead, we turn to find a probabilistic reachable set that bounds system states with confidence. A data-driven approach of Kernel Density Estimator (KDE) accelerated by Fast Fourier Transform (FFT) is customized to model the uncertainties and obtain the probabilistic reachable set efficiently. However, the irregular or non-convex shape of the probabilistic reachable set refrains it from practice. For the sake of real applications, we formulate an optimization problem as Mixed Integer Nonlinear Programming (MINLP) whose solution accounts for an optimal $n$-sided convex polygon to approximate the probabilistic reachable set. A heuristic algorithm is then developed to solve the MINLP efficiently while ensuring accuracy. The results of comprehensive case studies demonstrate the near-optimality, accuracy, efficiency, and robustness enjoyed by the proposed algorithm. The benefits of this work pave the way for its promising applications to safety-critical real-time motion planning of uncertain systems.

Risk-perception-aware control design under dynamic spatial risks

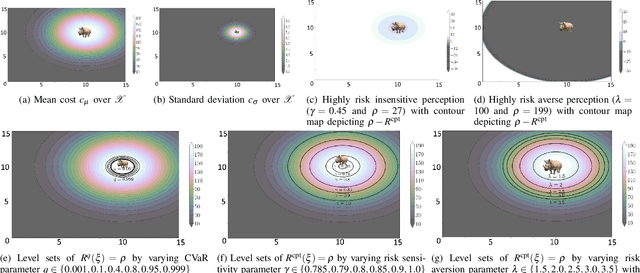
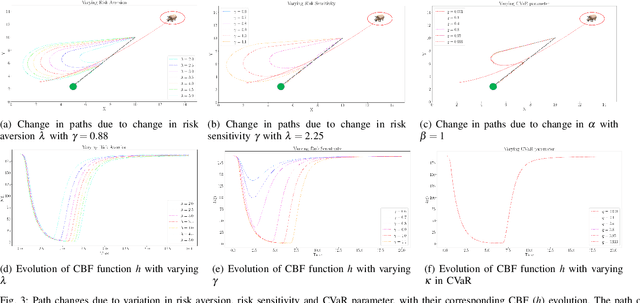
This work proposes a novel risk-perception-aware (RPA) control design using non-rational perception of risks associated with uncertain dynamic spatial costs. We use Cumulative Prospect Theory (CPT) to model the risk perception of a decision maker (DM) and use it to construct perceived risk functions that transform the uncertain dynamic spatial cost to deterministic perceived risks of a DM. These risks are then used to build safety sets which can represent risk-averse to risk-insensitive perception. We define a notions of "inclusiveness" and "versatility" based on safety sets and use it to compare with other models such as Conditional value at Risk (CVaR) and Expected risk (ER). We theoretically prove that CPT is the most "inclusive" and "versatile" model of the lot in the context of risk-perception-aware controls. We further use the perceived risk function along with ideas from control barrier functions (CBF) to construct a class of perceived risk CBFs. For a class of truncated-Gaussian costs, we find sufficient geometric conditions for the validity of this class of CBFs, thus guaranteeing safety. Then, we generate perceived-safety-critical controls using a Quadratic program (QP) to guide an agent safely according to a given perceived risk model. We present simulations in a 2D environment to illustrate the performance of the proposed controller.

Online Optimization and Learning in Uncertain Dynamical Environments with Performance Guarantees

We propose a new framework to solve online optimization and learning problems in unknown and uncertain dynamical environments. This framework enables us to simultaneously learn the uncertain dynamical environment while making online decisions in a quantifiably robust manner. The main technical approach relies on the theory of distributional robust optimization that leverages adaptive probabilistic ambiguity sets. However, as defined, the ambiguity set usually leads to online intractable problems, and the first part of our work is directed to find reformulations in the form of online convex problems for two sub-classes of objective functions. To solve the resulting problems in the proposed framework, we further introduce an online version of the Nesterov accelerated-gradient algorithm. We determine how the proposed solution system achieves a probabilistic regret bound under certain conditions. Two applications illustrate the applicability of the proposed framework.

Planning under risk and uncertainty based on Prospect-theoretic models

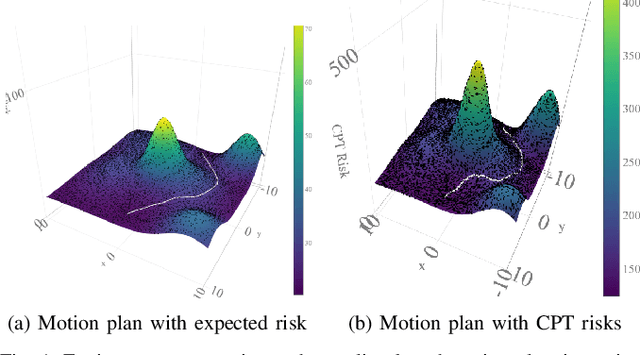
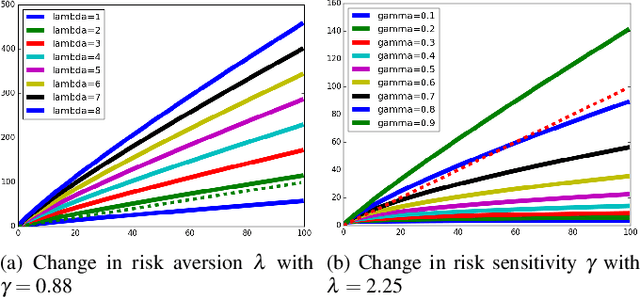
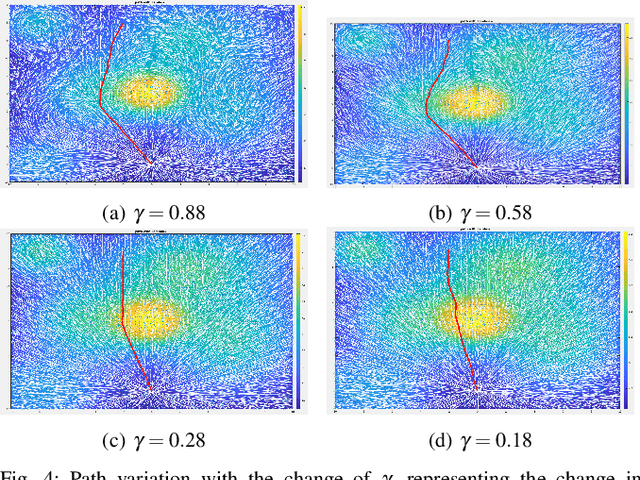
In this work, we develop a novel sampling-based motion planing approach to generate plans in a risky and uncertain environment. To model a variety of risk-sensitivity profiles, we propose an adaption of Cumulative Prospect Theory (CPT) to the setting of path planning. This leads to the definition of a non-rational continuous cost envelope (as well as a continuous uncertainty envelope) associated with an obstacle environment. We use these metrics along with standard costs like path length to formulate path planning problems. Building on RRT*, we then develop a sampling-based motion planner that generates desirable paths from the perspective of a given risk sensitive profile. Since risk sensitivity can greatly vary, we provide a tuning knob to appease a diversity of decision makers (DM), ranging from totally risk-averse to risk-indifferent. Additionally, we adapt a Simultaneous Perturbation Stochastic Approximation (SPSA)-based algorithm to learn the CPT parameters that can best represent a certain DM. Simulations are presented in a 2D environment to evaluate the modeling approach and algorithm's performance.

Gesture based Human-Swarm Interactions for Formation Control using interpreters

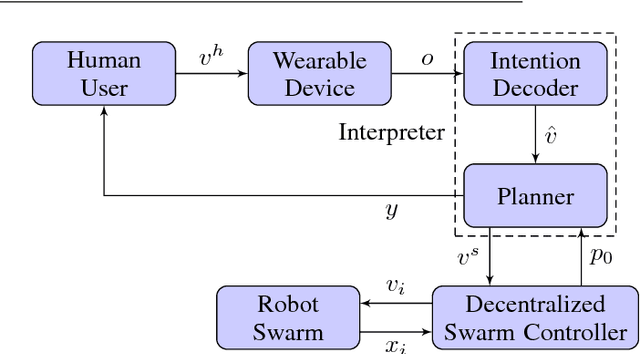
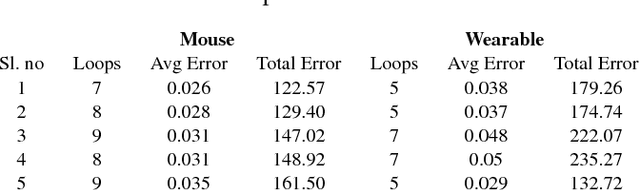
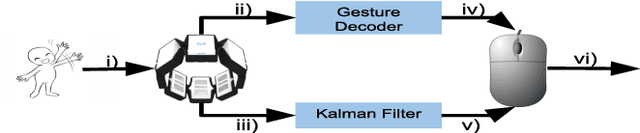
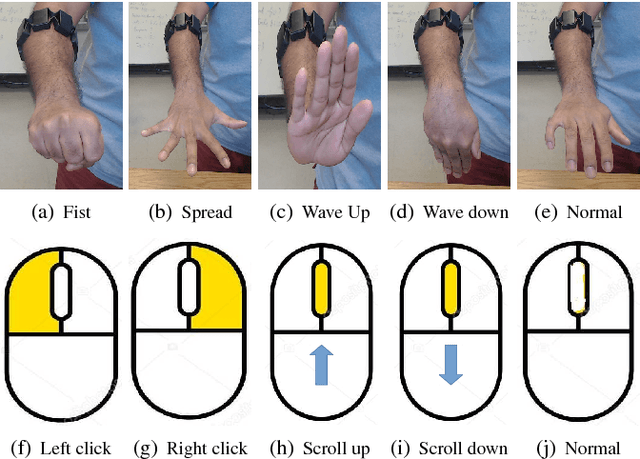
We propose a novel Human-Swarm Interaction (HSI) framework which enables the user to control a swarm shape and formation. The user commands the swarm utilizing just arm gestures and motions which are recorded by an off-the-shelf wearable armband. We propose a novel interpreter system, which acts as an intermediary between the user and the swarm to simplify the user's role in the interaction. The interpreter takes in a high level input drawn using gestures by the user, and translates it into low level swarm control commands. This interpreter employs machine learning, Kalman filtering and optimal control techniques to translate the user input into swarm control parameters. A notion of Human Interpretable dynamics is introduced, which is used by the interpreter for planning as well as to provide feedback to the user. The dynamics of the swarm are controlled using a novel decentralized formation controller based on distributed linear iterations and dynamic average consensus. The framework is demonstrated theoretically as well as experimentally in a 2D environment, with a human controlling a swarm of simulated robots in real time.