Planning under risk and uncertainty based on Prospect-theoretic models
Paper and Code
Apr 05, 2019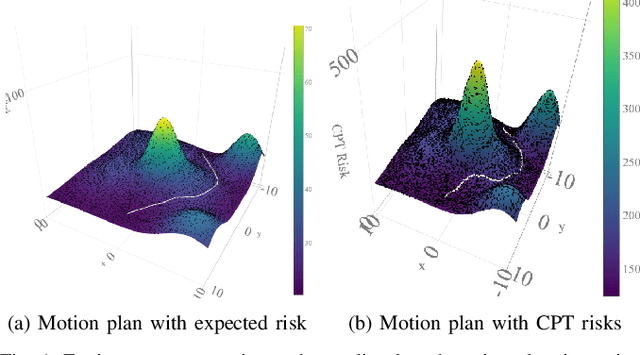
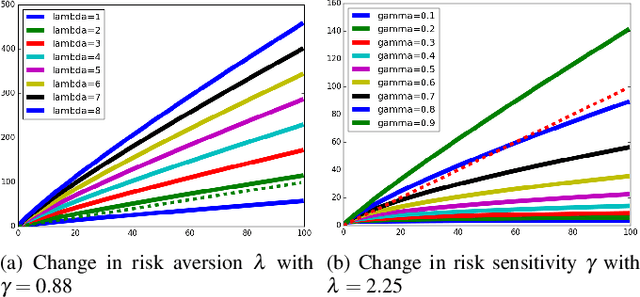

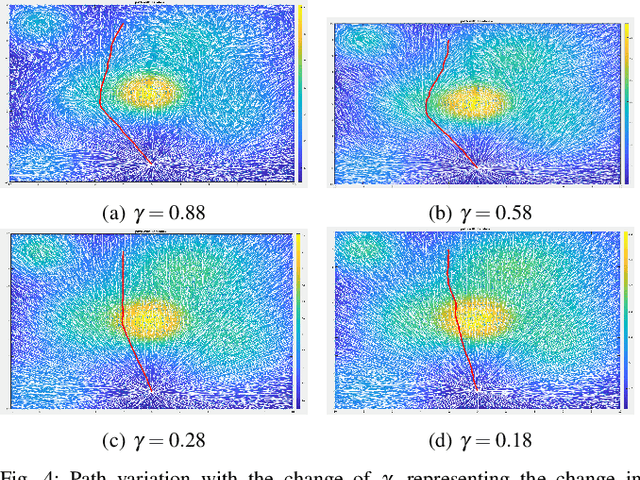
In this work, we develop a novel sampling-based motion planing approach to generate plans in a risky and uncertain environment. To model a variety of risk-sensitivity profiles, we propose an adaption of Cumulative Prospect Theory (CPT) to the setting of path planning. This leads to the definition of a non-rational continuous cost envelope (as well as a continuous uncertainty envelope) associated with an obstacle environment. We use these metrics along with standard costs like path length to formulate path planning problems. Building on RRT*, we then develop a sampling-based motion planner that generates desirable paths from the perspective of a given risk sensitive profile. Since risk sensitivity can greatly vary, we provide a tuning knob to appease a diversity of decision makers (DM), ranging from totally risk-averse to risk-indifferent. Additionally, we adapt a Simultaneous Perturbation Stochastic Approximation (SPSA)-based algorithm to learn the CPT parameters that can best represent a certain DM. Simulations are presented in a 2D environment to evaluate the modeling approach and algorithm's performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge