Adaptive Combinatorial Maximization: Beyond Approximate Greedy Policies

We study adaptive combinatorial maximization, which is a core challenge in machine learning, with applications in active learning as well as many other domains. We study the Bayesian setting, and consider the objectives of maximization under a cardinality constraint and minimum cost coverage. We provide new comprehensive approximation guarantees that subsume previous results, as well as considerably strengthen them. Our approximation guarantees simultaneously support the maximal gain ratio as well as near-submodular utility functions, and include both maximization under a cardinality constraint and a minimum cost coverage guarantee. In addition, we provided an approximation guarantee for a modified prior, which is crucial for obtaining active learning guarantees that do not depend on the smallest probability in the prior. Moreover, we discover a new parameter of adaptive selection policies, which we term the "maximal gain ratio". We show that this parameter is strictly less restrictive than the greedy approximation parameter that has been used in previous approximation guarantees, and show that it can be used to provide stronger approximation guarantees than previous results. In particular, we show that the maximal gain ratio is never larger than the greedy approximation factor of a policy, and that it can be considerably smaller. This provides a new insight into the properties that make a policy useful for adaptive combinatorial maximization.

On the Capacity Limits of Privileged ERM

We study the supervised learning paradigm called Learning Using Privileged Information, first suggested by Vapnik and Vashist (2009). In this paradigm, in addition to the examples and labels, additional (privileged) information is provided only for training examples. The goal is to use this information to improve the classification accuracy of the resulting classifier, where this classifier can only use the non-privileged information of new example instances to predict their label. We study the theory of privileged learning with the zero-one loss under the natural Privileged ERM algorithm proposed in Pechyony and Vapnik (2010a). We provide a counter example to a claim made in that work regarding the VC dimension of the loss class induced by this problem; We conclude that the claim is incorrect. We then provide a correct VC dimension analysis which gives both lower and upper bounds on the capacity of the Privileged ERM loss class. We further show, via a generalization analysis, that worst-case guarantees for Privileged ERM cannot improve over standard non-privileged ERM, unless the capacity of the privileged information is similar or smaller to that of the non-privileged information. This result points to an important limitation of the Privileged ERM approach. In our closing discussion, we suggest another way in which Privileged ERM might still be helpful, even when the capacity of the privileged information is large.

Improved Robust Algorithms for Learning with Discriminative Feature Feedback

Discriminative Feature Feedback is a setting proposed by Dastupta et al. (2018), which provides a protocol for interactive learning based on feature explanations that are provided by a human teacher. The features distinguish between the labels of pairs of possibly similar instances. That work has shown that learning in this model can have considerable statistical and computational advantages over learning in standard label-based interactive learning models. In this work, we provide new robust interactive learning algorithms for the Discriminative Feature Feedback model, with mistake bounds that are significantly lower than those of previous robust algorithms for this setting. In the adversarial setting, we reduce the dependence on the number of protocol exceptions from quadratic to linear. In addition, we provide an algorithm for a slightly more restricted model, which obtains an even smaller mistake bound for large models with many exceptions. In the stochastic setting, we provide the first algorithm that converges to the exception rate with a polynomial sample complexity. Our algorithm and analysis for the stochastic setting involve a new construction that we call Feature Influence, which may be of wider applicability.

Inferring Unfairness and Error from Population Statistics in Binary and Multiclass Classification

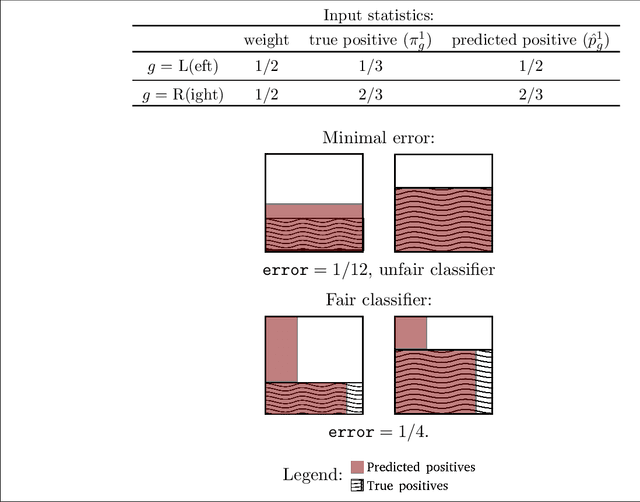
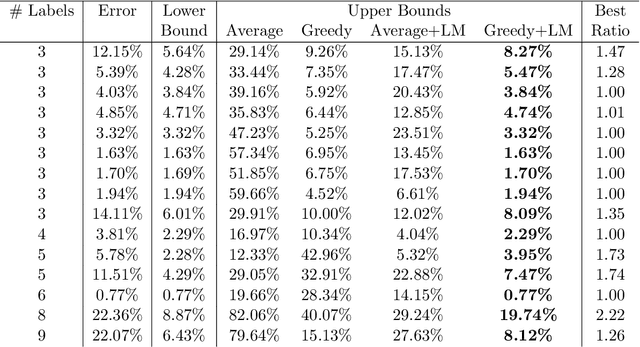
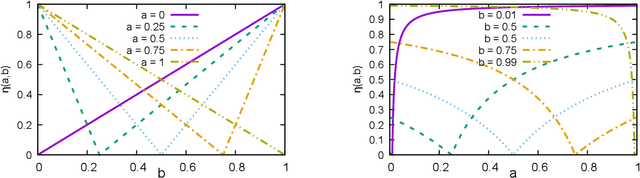
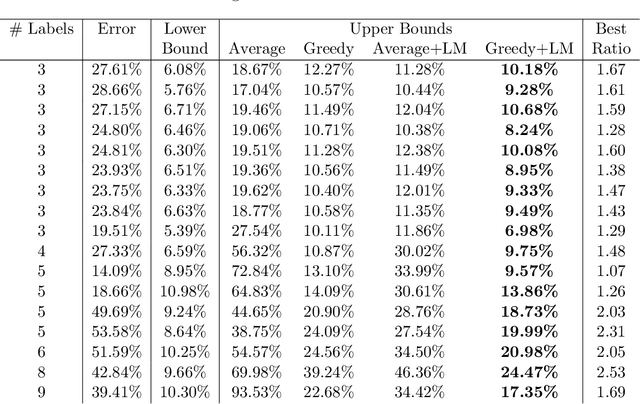
We propose methods for making inferences on the fairness and accuracy of a given classifier, using only aggregate population statistics. This is necessary when it is impossible to obtain individual classification data, for instance when there is no access to the classifier or to a representative individual-level validation set. We study fairness with respect to the equalized odds criterion, which we generalize to multiclass classification. We propose a measure of unfairness with respect to this criterion, which quantifies the fraction of the population that is treated unfairly. We then show how inferences on the unfairness and error of a given classifier can be obtained using only aggregate label statistics such as the rate of prediction of each label in each sub-population, as well as the true rate of each label. We derive inference procedures for binary classifiers and for multiclass classifiers, for the case where confusion matrices in each sub-population are known, and for the significantly more challenging case where they are unknown. We report experiments on data sets representing diverse applications, which demonstrate the effectiveness and the wide range of possible uses of the proposed methodology.

Fast Distributed k-Means with a Small Number of Rounds

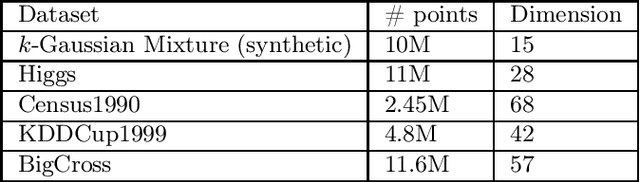
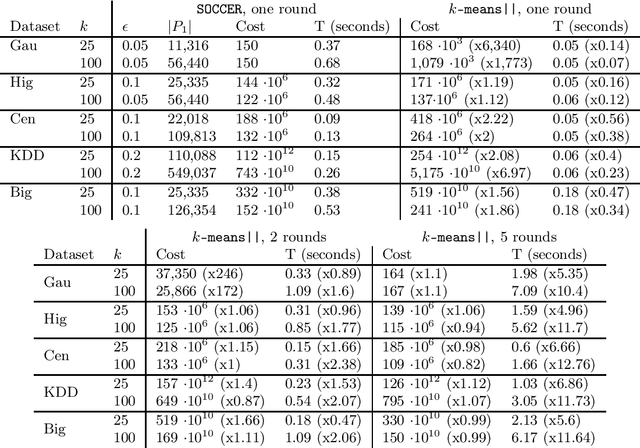
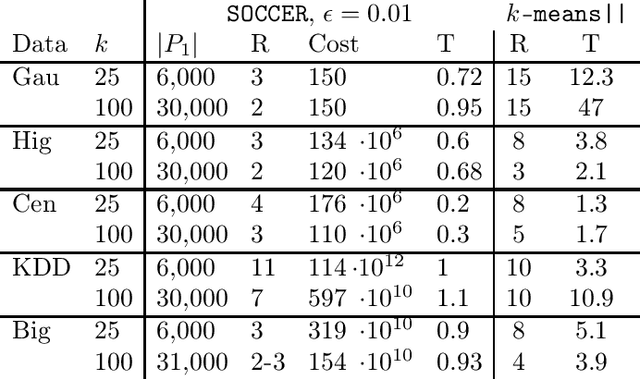
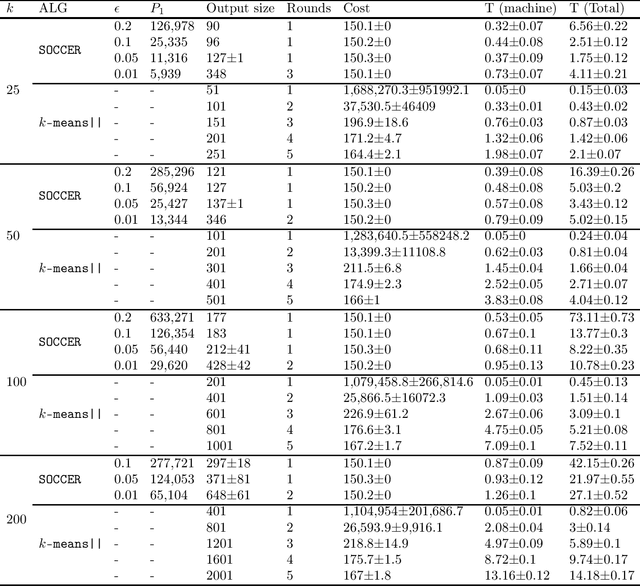
We propose a new algorithm for k-means clustering in a distributed setting, where the data is distributed across many machines, and a coordinator communicates with these machines to calculate the output clustering. Our algorithm guarantees a cost approximation factor and a number of communication rounds that depend only on the computational capacity of the coordinator. Moreover, the algorithm includes a built-in stopping mechanism, which allows it to use fewer communication rounds whenever possible. We show both theoretically and empirically that in many natural cases, indeed 1-4 rounds suffice. In comparison with the popular k-means|| algorithm, our approach allows exploiting a larger coordinator capacity to obtain a smaller number of rounds. Our experiments show that the k-means cost obtained by the proposed algorithm is usually better than the cost obtained by k-means||, even when the latter is allowed a larger number of rounds. Moreover, the machine running time in our approach is considerably smaller than that of k-means||. Code for running the algorithm and experiments is available at https://github.com/selotape/distributed_k_means.

A Fast Algorithm for PAC Combinatorial Pure Exploration

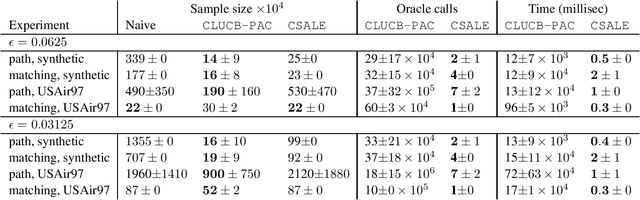
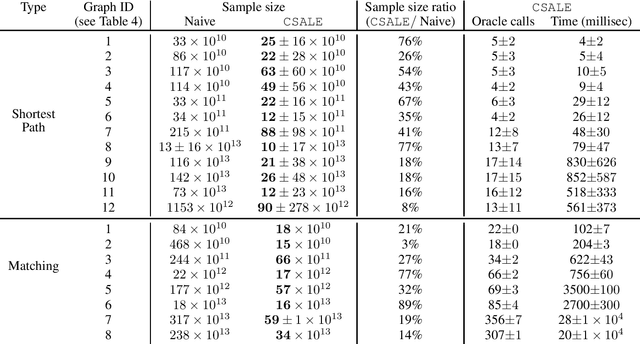
We consider the problem of Combinatorial Pure Exploration (CPE), which deals with finding a combinatorial set or arms with a high reward, when the rewards of individual arms are unknown in advance and must be estimated using arm pulls. Previous algorithms for this problem, while obtaining sample complexity reductions in many cases, are highly computationally intensive, thus making them impractical even for mildly large problems. In this work, we propose a new CPE algorithm in the PAC setting, which is computationally light weight, and so can easily be applied to problems with tens of thousands of arms. This is achieved since the proposed algorithm requires a very small number of combinatorial oracle calls. The algorithm is based on successive acceptance of arms, along with elimination which is based on the combinatorial structure of the problem. We provide sample complexity guarantees for our algorithm, and demonstrate in experiments its usefulness on large problems, whereas previous algorithms are impractical to run on problems of even a few dozen arms. The code for the algorithms and experiments is provided at https://github.com/noabdavid/csale.

Active Structure Learning of Bayesian Networks in an Observational Setting

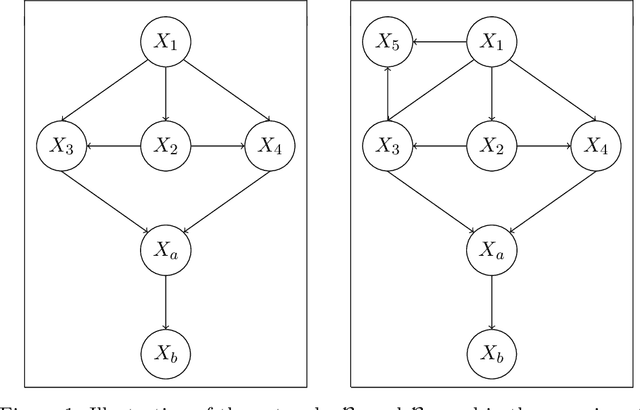
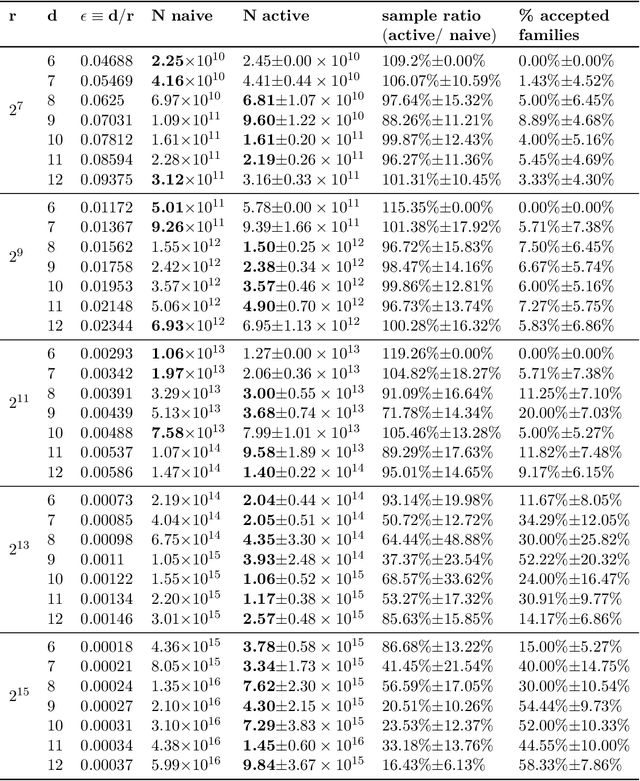
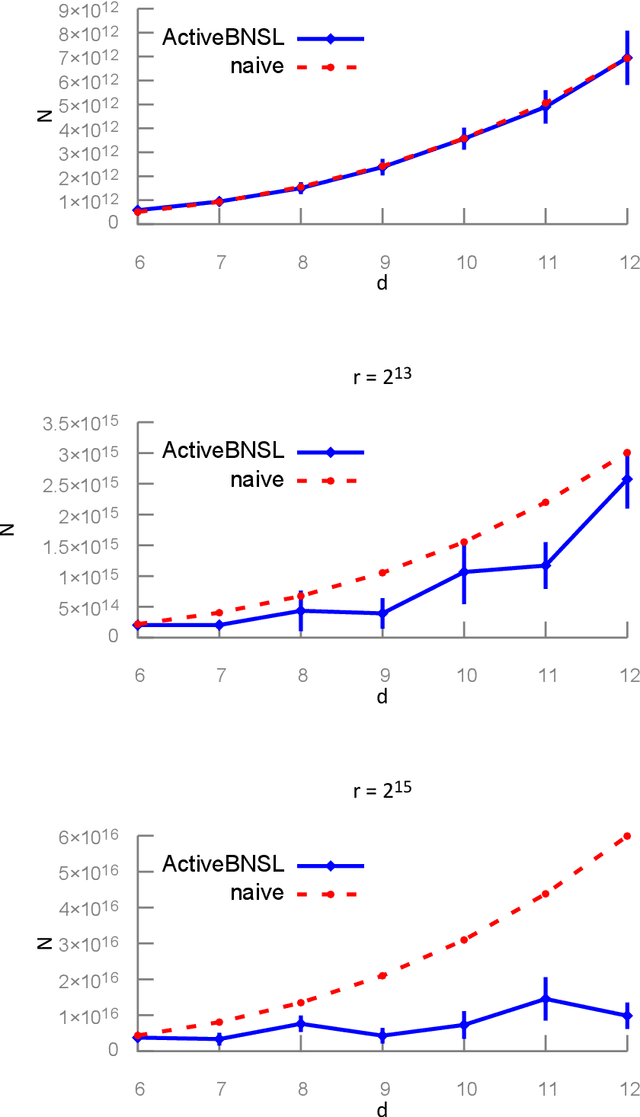
We study active structure learning of Bayesian networks in an observational setting, in which there are external limitations on the number of variable values that can be observed from the same sample. Random samples are drawn from the joint distribution of the network variables, and the algorithm iteratively selects which variables to observe in the next sample. We propose a new active learning algorithm for this setting, that finds with a high probability a structure with a score that is $\epsilon$-close to the optimal score. We show that for a class of distributions that we term stable, a sample complexity reduction of up to a factor of $\widetilde{\Omega}(d^3)$ can be obtained, where $d$ is the number of network variables. We further show that in the worst case, the sample complexity of the active algorithm is guaranteed to be almost the same as that of a naive baseline algorithm. To supplement the theoretical results, we report experiments that compare the performance of the new active algorithm to the naive baseline and demonstrate the sample complexity improvements. Code for the algorithm and for the experiments is provided at https://github.com/noabdavid/activeBNSL.

A Constant Approximation Algorithm for Sequential No-Substitution k-Median Clustering under a Random Arrival Order

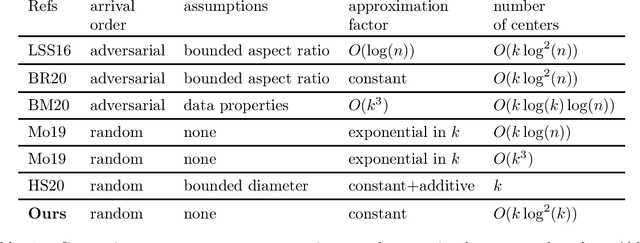
We study k-median clustering under the sequential no-substitution setting. In this setting, a data stream is sequentially observed, and some of the points are selected by the algorithm as cluster centers. However, a point can be selected as a center only immediately after it is observed, before observing the next point. In addition, a selected center cannot be substituted later. We give a new algorithm for this setting that obtains a constant approximation factor on the optimal risk under a random arrival order. This is the first such algorithm that holds without any assumptions on the input data and selects a non-trivial number of centers. The number of selected centers is quasi-linear in k. Our algorithm and analysis are based on a careful risk estimation that avoids outliers, a new concept of a linear bin division, and repeated calculations using an offline clustering algorithm.

Active Feature Selection for the Mutual Information Criterion

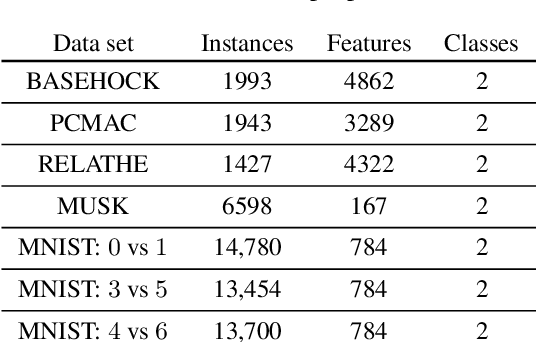
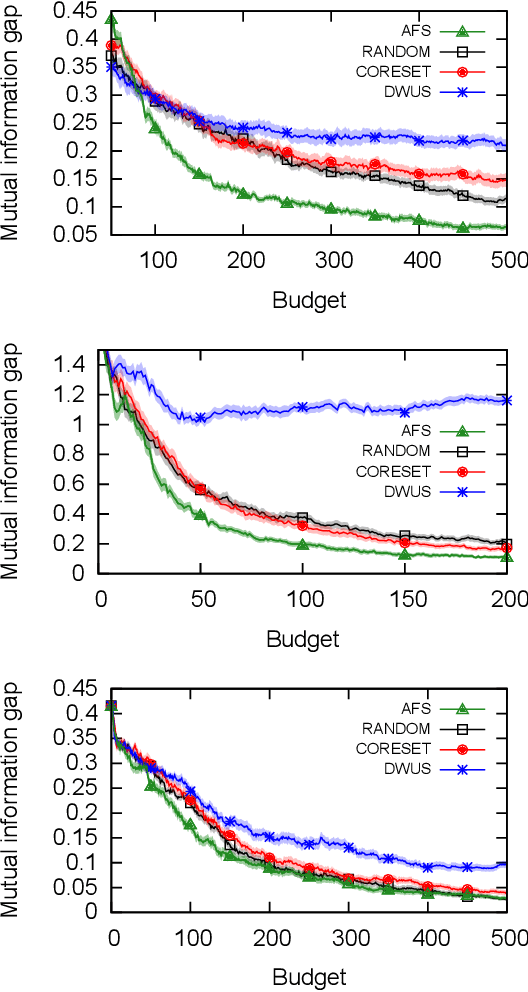
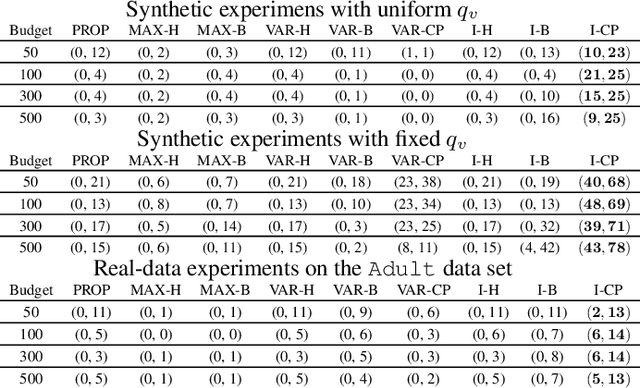
We study active feature selection, a novel feature selection setting in which unlabeled data is available, but the budget for labels is limited, and the examples to label can be actively selected by the algorithm. We focus on feature selection using the classical mutual information criterion, which selects the $k$ features with the largest mutual information with the label. In the active feature selection setting, the goal is to use significantly fewer labels than the data set size and still find $k$ features whose mutual information with the label based on the \emph{entire} data set is large. We explain and experimentally study the choices that we make in the algorithm, and show that they lead to a successful algorithm, compared to other more naive approaches. Our design draws on insights which relate the problem of active feature selection to the study of pure-exploration multi-armed bandits settings. While we focus here on mutual information, our general methodology can be adapted to other feature-quality measures as well. The code is available at the following url: https://github.com/ShacharSchnapp/ActiveFeatureSelection.

Approximating a Target Distribution using Weight Queries

A basic assumption in classical learning and estimation is the availability of a random sample from the target distribution. In domain adaptation this assumption is replaced with the availability of a sample from a source distribution, and a smaller or unlabeled sample from the target distribution. In this work, we consider a setting in which no random sampling from the target distribution is possible. Instead, given a large data set, it is possible to query the probability (weight) of a data point, or a set of data points, according to the target distribution. This can be the case when access to the target distribution is mediated, e.g., by specific measurements or by user relevance queries. We propose an algorithm for finding a reweighing of the data set which approximates the target distribution weights, using a limited number of target weight queries. The weighted data set may then be used in estimation and learning tasks, as a proxy for a sample from the target distribution. Given a hierarchical tree structure over the data set, which induces a class of weight functions, we prove that the algorithm approximates the best possible function, and upper bound the number of weight queries. In experiments, we demonstrate the advantage of the proposed algorithm over several baselines. A python implementation of the proposed algorithm and all experiments can be found at https://github.com/Nadav-Barak/AWP.