Shachar Schnapp
Differentially Private Approximate Quantiles
Oct 11, 2021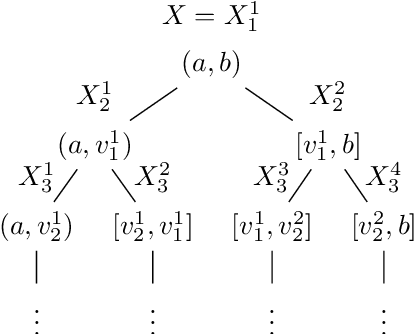
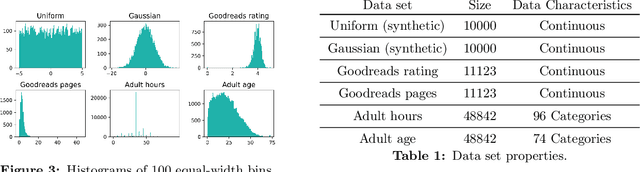
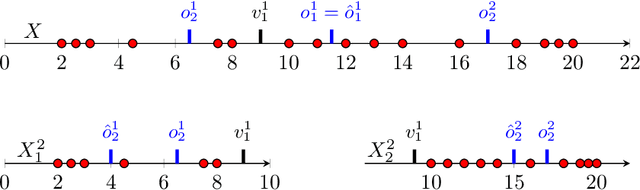
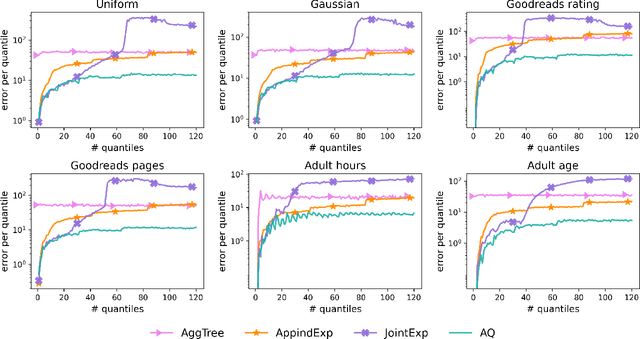
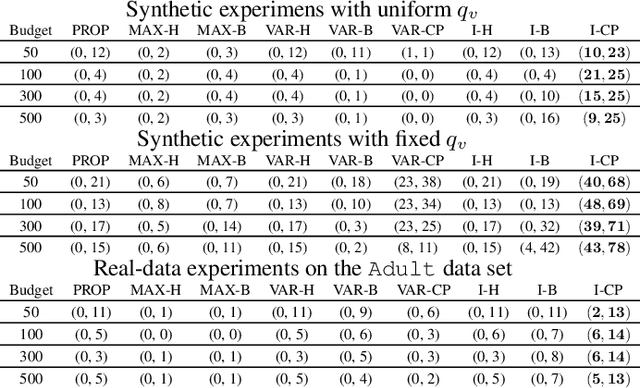
Abstract:In this work we study the problem of differentially private (DP) quantiles, in which given dataset $X$ and quantiles $q_1, ..., q_m \in [0,1]$, we want to output $m$ quantile estimations which are as close as possible to the true quantiles and preserve DP. We describe a simple recursive DP algorithm, which we call ApproximateQuantiles (AQ), for this task. We give a worst case upper bound on its error, and show that its error is much lower than of previous implementations on several different datasets. Furthermore, it gets this low error while running time two orders of magnitude faster that the best previous implementation.
Active Feature Selection for the Mutual Information Criterion
Dec 13, 2020
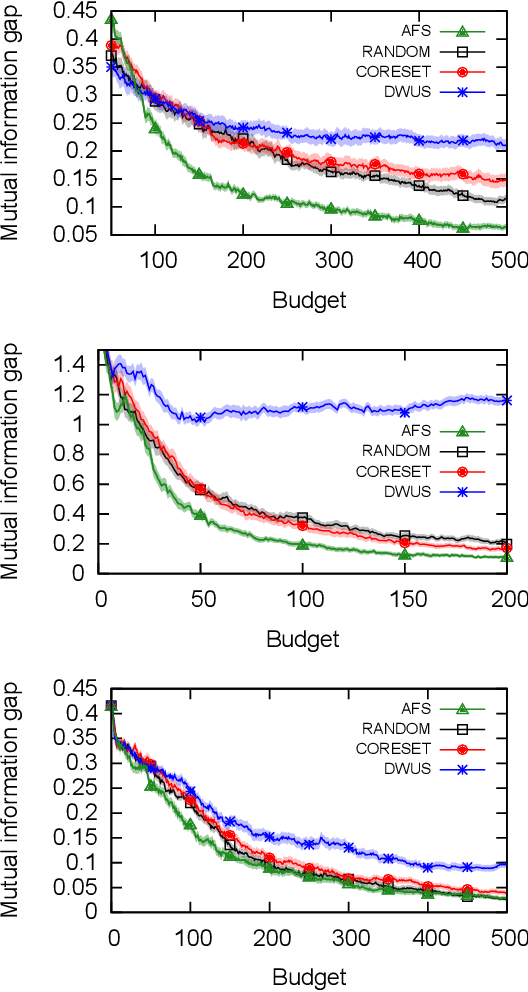
Abstract:We study active feature selection, a novel feature selection setting in which unlabeled data is available, but the budget for labels is limited, and the examples to label can be actively selected by the algorithm. We focus on feature selection using the classical mutual information criterion, which selects the $k$ features with the largest mutual information with the label. In the active feature selection setting, the goal is to use significantly fewer labels than the data set size and still find $k$ features whose mutual information with the label based on the \emph{entire} data set is large. We explain and experimentally study the choices that we make in the algorithm, and show that they lead to a successful algorithm, compared to other more naive approaches. Our design draws on insights which relate the problem of active feature selection to the study of pure-exploration multi-armed bandits settings. While we focus here on mutual information, our general methodology can be adapted to other feature-quality measures as well. The code is available at the following url: https://github.com/ShacharSchnapp/ActiveFeatureSelection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge