Differentially Private Approximate Quantiles
Paper and Code
Oct 11, 2021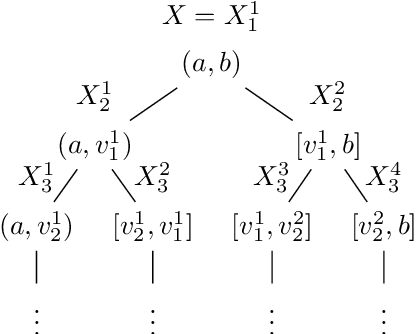
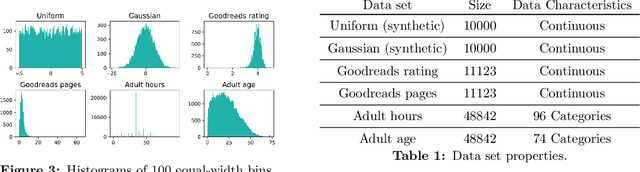
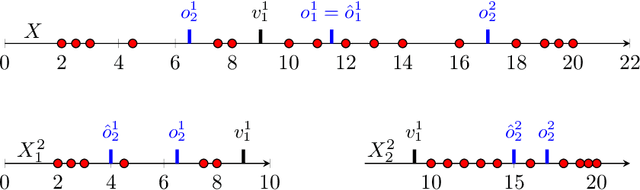
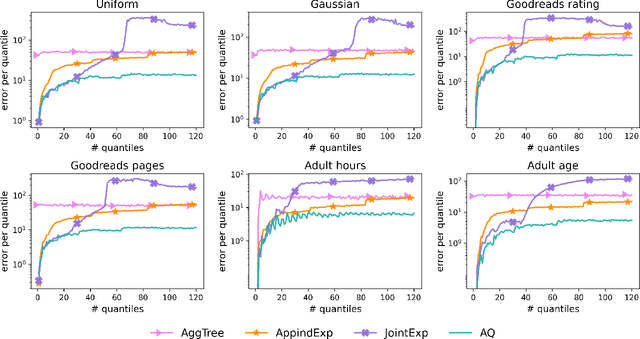
In this work we study the problem of differentially private (DP) quantiles, in which given dataset $X$ and quantiles $q_1, ..., q_m \in [0,1]$, we want to output $m$ quantile estimations which are as close as possible to the true quantiles and preserve DP. We describe a simple recursive DP algorithm, which we call ApproximateQuantiles (AQ), for this task. We give a worst case upper bound on its error, and show that its error is much lower than of previous implementations on several different datasets. Furthermore, it gets this low error while running time two orders of magnitude faster that the best previous implementation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge