Active Structure Learning of Bayesian Networks in an Observational Setting
Paper and Code
Mar 25, 2021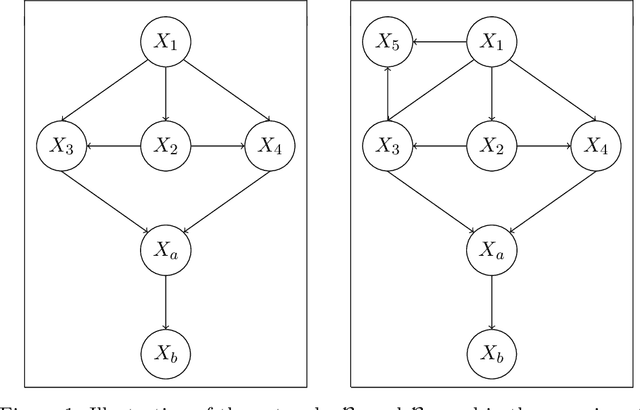
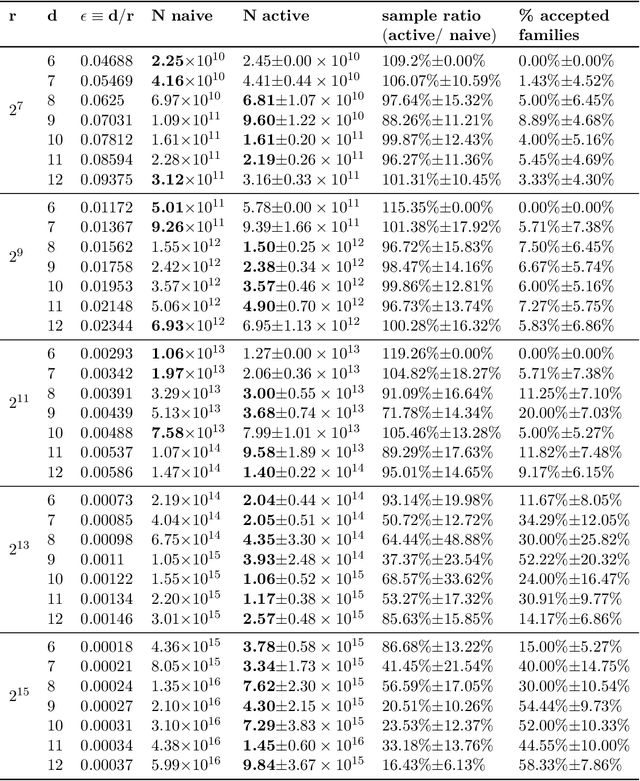
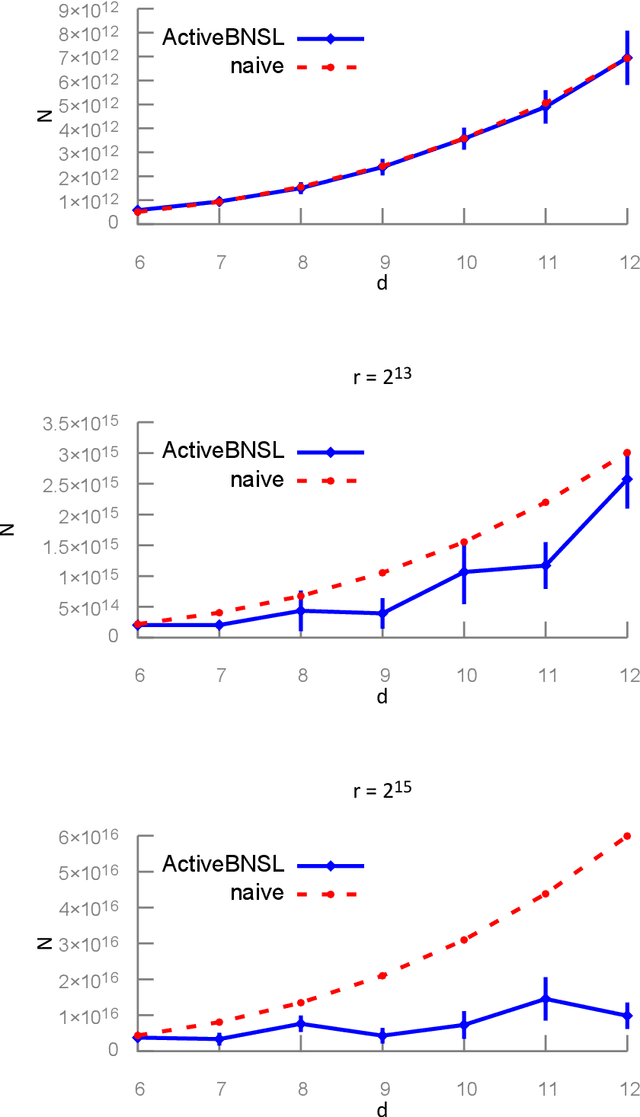
We study active structure learning of Bayesian networks in an observational setting, in which there are external limitations on the number of variable values that can be observed from the same sample. Random samples are drawn from the joint distribution of the network variables, and the algorithm iteratively selects which variables to observe in the next sample. We propose a new active learning algorithm for this setting, that finds with a high probability a structure with a score that is $\epsilon$-close to the optimal score. We show that for a class of distributions that we term stable, a sample complexity reduction of up to a factor of $\widetilde{\Omega}(d^3)$ can be obtained, where $d$ is the number of network variables. We further show that in the worst case, the sample complexity of the active algorithm is guaranteed to be almost the same as that of a naive baseline algorithm. To supplement the theoretical results, we report experiments that compare the performance of the new active algorithm to the naive baseline and demonstrate the sample complexity improvements. Code for the algorithm and for the experiments is provided at https://github.com/noabdavid/activeBNSL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge