A Fast Algorithm for PAC Combinatorial Pure Exploration

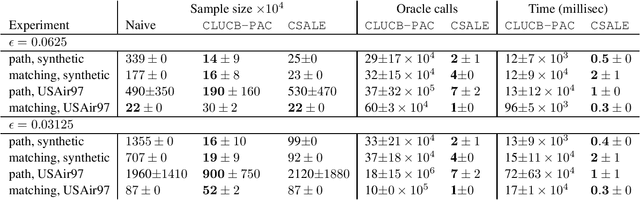
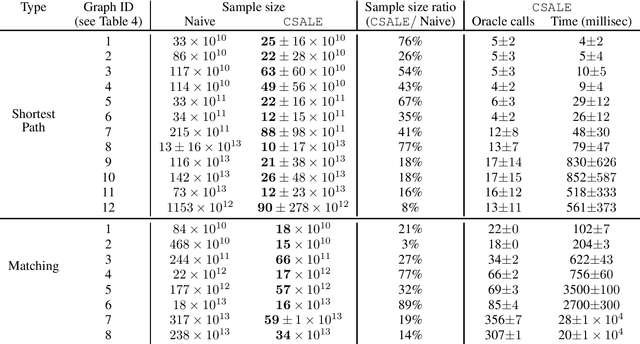
We consider the problem of Combinatorial Pure Exploration (CPE), which deals with finding a combinatorial set or arms with a high reward, when the rewards of individual arms are unknown in advance and must be estimated using arm pulls. Previous algorithms for this problem, while obtaining sample complexity reductions in many cases, are highly computationally intensive, thus making them impractical even for mildly large problems. In this work, we propose a new CPE algorithm in the PAC setting, which is computationally light weight, and so can easily be applied to problems with tens of thousands of arms. This is achieved since the proposed algorithm requires a very small number of combinatorial oracle calls. The algorithm is based on successive acceptance of arms, along with elimination which is based on the combinatorial structure of the problem. We provide sample complexity guarantees for our algorithm, and demonstrate in experiments its usefulness on large problems, whereas previous algorithms are impractical to run on problems of even a few dozen arms. The code for the algorithms and experiments is provided at https://github.com/noabdavid/csale.

Active Structure Learning of Bayesian Networks in an Observational Setting

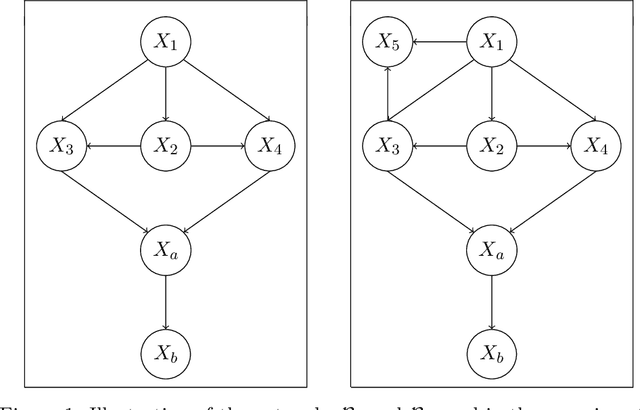
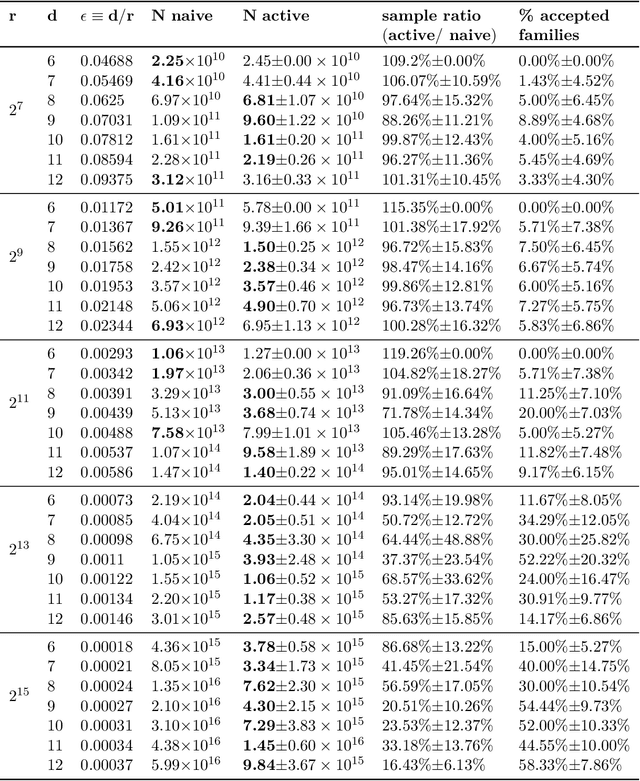
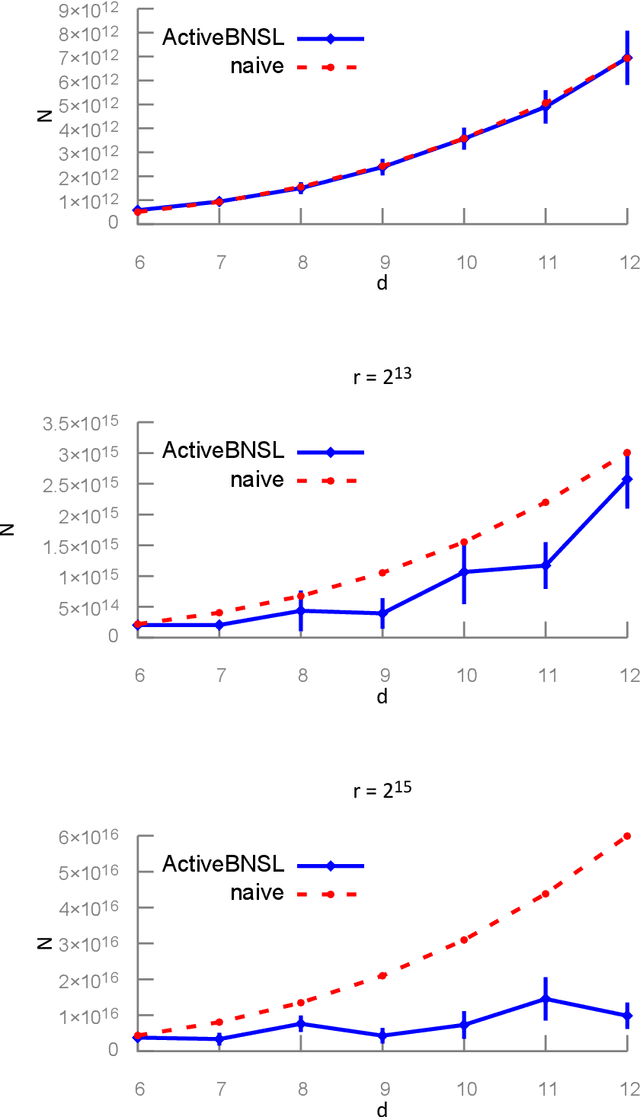
We study active structure learning of Bayesian networks in an observational setting, in which there are external limitations on the number of variable values that can be observed from the same sample. Random samples are drawn from the joint distribution of the network variables, and the algorithm iteratively selects which variables to observe in the next sample. We propose a new active learning algorithm for this setting, that finds with a high probability a structure with a score that is $\epsilon$-close to the optimal score. We show that for a class of distributions that we term stable, a sample complexity reduction of up to a factor of $\widetilde{\Omega}(d^3)$ can be obtained, where $d$ is the number of network variables. We further show that in the worst case, the sample complexity of the active algorithm is guaranteed to be almost the same as that of a naive baseline algorithm. To supplement the theoretical results, we report experiments that compare the performance of the new active algorithm to the naive baseline and demonstrate the sample complexity improvements. Code for the algorithm and for the experiments is provided at https://github.com/noabdavid/activeBNSL.