Inferring Unfairness and Error from Population Statistics in Binary and Multiclass Classification
Paper and Code
Jun 07, 2022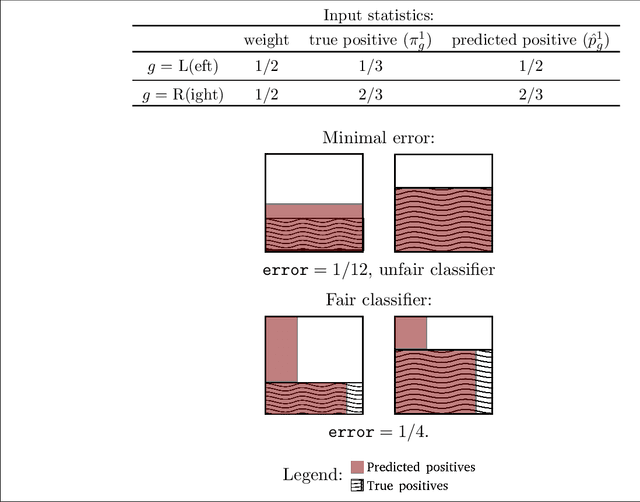
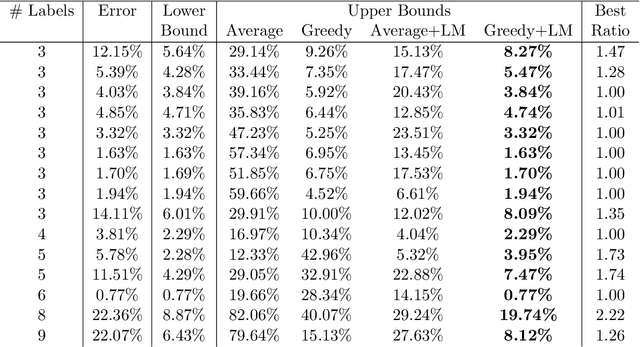
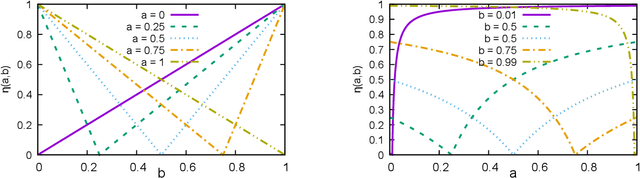
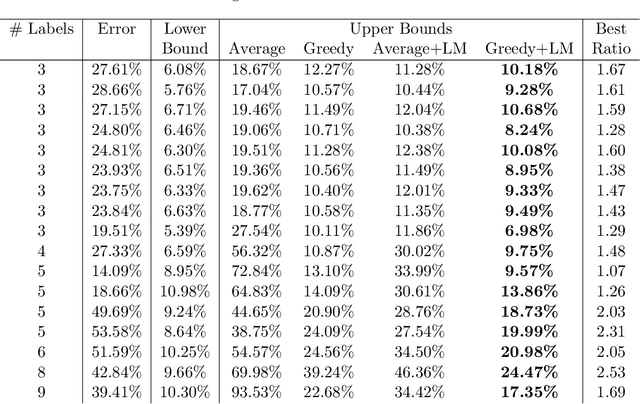
We propose methods for making inferences on the fairness and accuracy of a given classifier, using only aggregate population statistics. This is necessary when it is impossible to obtain individual classification data, for instance when there is no access to the classifier or to a representative individual-level validation set. We study fairness with respect to the equalized odds criterion, which we generalize to multiclass classification. We propose a measure of unfairness with respect to this criterion, which quantifies the fraction of the population that is treated unfairly. We then show how inferences on the unfairness and error of a given classifier can be obtained using only aggregate label statistics such as the rate of prediction of each label in each sub-population, as well as the true rate of each label. We derive inference procedures for binary classifiers and for multiclass classifiers, for the case where confusion matrices in each sub-population are known, and for the significantly more challenging case where they are unknown. We report experiments on data sets representing diverse applications, which demonstrate the effectiveness and the wide range of possible uses of the proposed methodology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge