Fast Distributed k-Means with a Small Number of Rounds

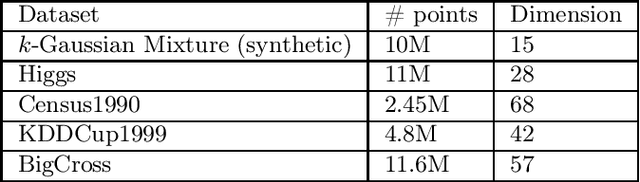
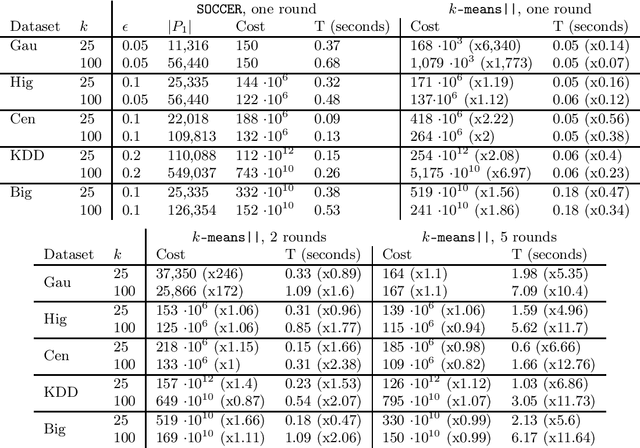
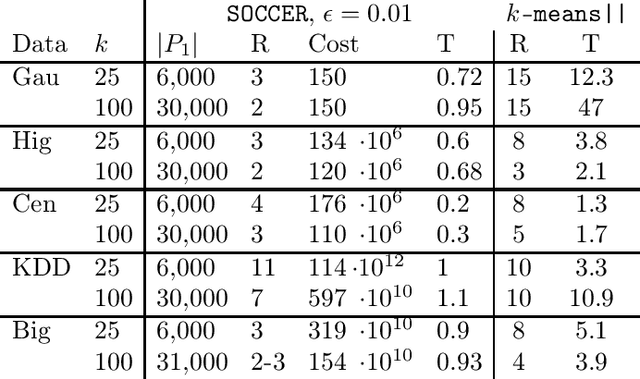
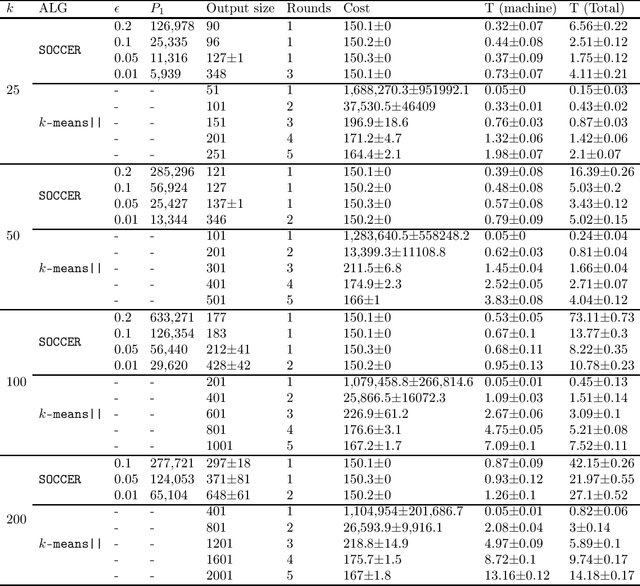
We propose a new algorithm for k-means clustering in a distributed setting, where the data is distributed across many machines, and a coordinator communicates with these machines to calculate the output clustering. Our algorithm guarantees a cost approximation factor and a number of communication rounds that depend only on the computational capacity of the coordinator. Moreover, the algorithm includes a built-in stopping mechanism, which allows it to use fewer communication rounds whenever possible. We show both theoretically and empirically that in many natural cases, indeed 1-4 rounds suffice. In comparison with the popular k-means|| algorithm, our approach allows exploiting a larger coordinator capacity to obtain a smaller number of rounds. Our experiments show that the k-means cost obtained by the proposed algorithm is usually better than the cost obtained by k-means||, even when the latter is allowed a larger number of rounds. Moreover, the machine running time in our approach is considerably smaller than that of k-means||. Code for running the algorithm and experiments is available at https://github.com/selotape/distributed_k_means.

A Constant Approximation Algorithm for Sequential No-Substitution k-Median Clustering under a Random Arrival Order

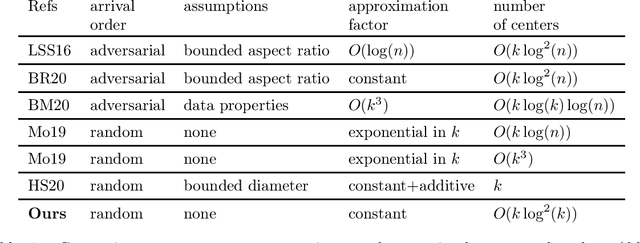
We study k-median clustering under the sequential no-substitution setting. In this setting, a data stream is sequentially observed, and some of the points are selected by the algorithm as cluster centers. However, a point can be selected as a center only immediately after it is observed, before observing the next point. In addition, a selected center cannot be substituted later. We give a new algorithm for this setting that obtains a constant approximation factor on the optimal risk under a random arrival order. This is the first such algorithm that holds without any assumptions on the input data and selects a non-trivial number of centers. The number of selected centers is quasi-linear in k. Our algorithm and analysis are based on a careful risk estimation that avoids outliers, a new concept of a linear bin division, and repeated calculations using an offline clustering algorithm.

Sequential no-Substitution k-Median-Clustering

We study the sample-based $k$-median clustering objective under a sequential setting without substitutions. In this setting, the goal is to select k centers that approximate the optimal clustering on an unknown distribution from a finite sequence of i.i.d. samples, where any selection of a center must be done immediately after the center is observed and centers cannot be substituted after selection. We provide an efficient algorithm for this setting, and show that its multiplicative approximation factor is twice the approximation factor of an efficient offline algorithm. In addition, we show that if efficiency requirements are removed, there is an algorithm that can obtain the same approximation factor as the best offline algorithm.

Interactive algorithms: from pool to stream

We consider interactive algorithms in the pool-based setting, and in the stream-based setting. Interactive algorithms observe suggested elements (representing actions or queries), and interactively select some of them and receive responses. Pool-based algorithms can select elements at any order, while stream-based algorithms observe elements in sequence, and can only select elements immediately after observing them. We assume that the suggested elements are generated independently from some source distribution, and ask what is the stream size required for emulating a pool algorithm with a given pool size. We provide algorithms and matching lower bounds for general pool algorithms, and for utility-based pool algorithms. We further show that a maximal gap between the two settings exists also in the special case of active learning for binary classification.