SememeLM: A Sememe Knowledge Enhanced Method for Long-tail Relation Representation

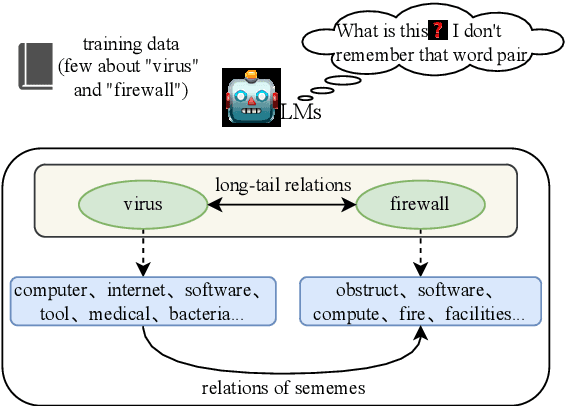
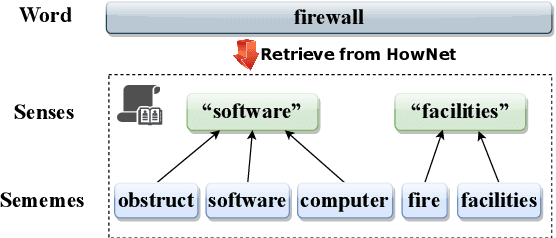
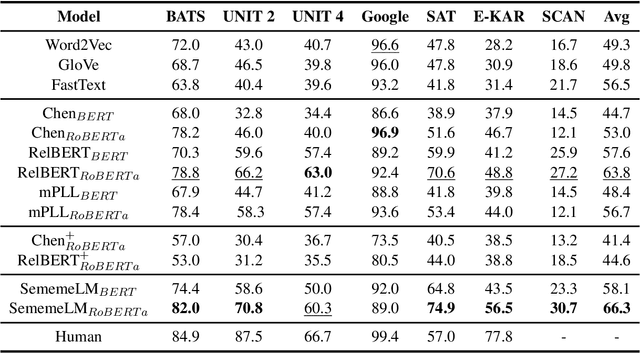
Recognizing relations between two words is a fundamental task with the broad applications. Different from extracting relations from text, it is difficult to identify relations among words without their contexts. Especially for long-tail relations, it becomes more difficult due to inadequate semantic features. Existing approaches based on language models (LMs) utilize rich knowledge of LMs to enhance the semantic features of relations. However, they capture uncommon relations while overlooking less frequent but meaningful ones since knowledge of LMs seriously relies on trained data where often represents common relations. On the other hand, long-tail relations are often uncommon in training data. It is interesting but not trivial to use external knowledge to enrich LMs due to collecting corpus containing long-tail relationships is hardly feasible. In this paper, we propose a sememe knowledge enhanced method (SememeLM) to enhance the representation of long-tail relations, in which sememes can break the contextual constraints between wors. Firstly, we present a sememe relation graph and propose a graph encoding method. Moreover, since external knowledge base possibly consisting of massive irrelevant knowledge, the noise is introduced. We propose a consistency alignment module, which aligns the introduced knowledge with LMs, reduces the noise and integrates the knowledge into the language model. Finally, we conducted experiments on word analogy datasets, which evaluates the ability to distinguish relation representations subtle differences, including long-tail relations. Extensive experiments show that our approach outperforms some state-of-the-art methods.

Spatiotemporal Besov Priors for Bayesian Inverse Problems

Fast development in science and technology has driven the need for proper statistical tools to capture special data features such as abrupt changes or sharp contrast. Many applications in the data science seek spatiotemporal reconstruction from a sequence of time-dependent objects with discontinuity or singularity, e.g. dynamic computerized tomography (CT) images with edges. Traditional methods based on Gaussian processes (GP) may not provide satisfactory solutions since they tend to offer over-smooth prior candidates. Recently, Besov process (BP) defined by wavelet expansions with random coefficients has been proposed as a more appropriate prior for this type of Bayesian inverse problems. While BP outperforms GP in imaging analysis to produce edge-preserving reconstructions, it does not automatically incorporate temporal correlation inherited in the dynamically changing images. In this paper, we generalize BP to the spatiotemporal domain (STBP) by replacing the random coefficients in the series expansion with stochastic time functions following Q-exponential process which governs the temporal correlation strength. Mathematical and statistical properties about STBP are carefully studied. A white-noise representation of STBP is also proposed to facilitate the point estimation through maximum a posterior (MAP) and the uncertainty quantification (UQ) by posterior sampling. Two limited-angle CT reconstruction examples and a highly non-linear inverse problem involving Navier-Stokes equation are used to demonstrate the advantage of the proposed STBP in preserving spatial features while accounting for temporal changes compared with the classic STGP and a time-uncorrelated approach.

Bayesian Regularization on Function Spaces via Q-Exponential Process

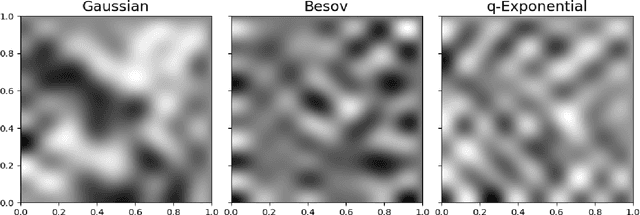
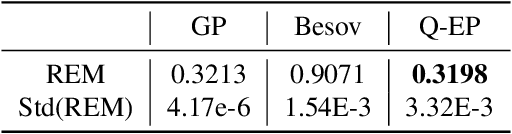
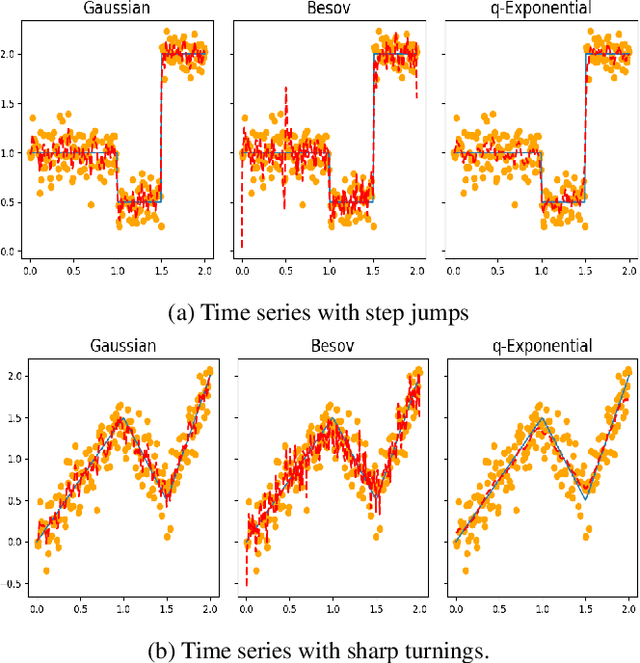
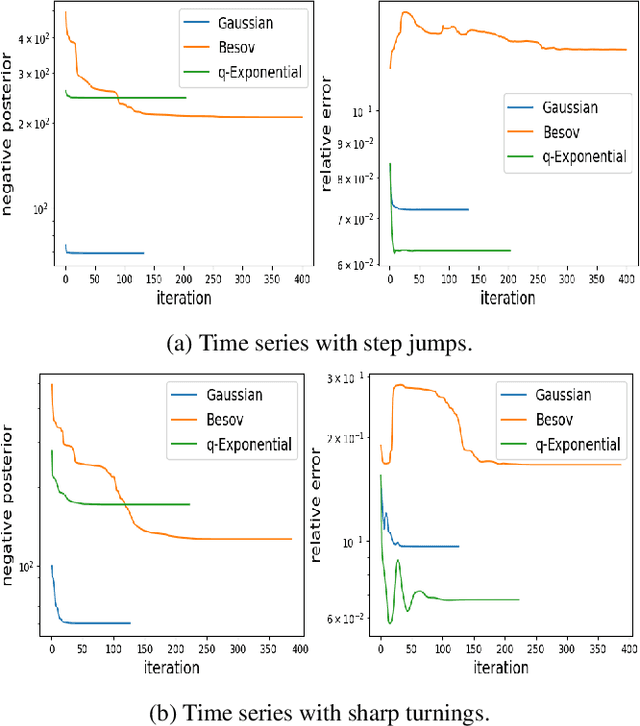
Regularization is one of the most important topics in optimization, statistics and machine learning. To get sparsity in estimating a parameter $u\in\mbR^d$, an $\ell_q$ penalty term, $\Vert u\Vert_q$, is usually added to the objective function. What is the probabilistic distribution corresponding to such $\ell_q$ penalty? What is the correct stochastic process corresponding to $\Vert u\Vert_q$ when we model functions $u\in L^q$? This is important for statistically modeling large dimensional objects, e.g. images, with penalty to preserve certainty properties, e.g. edges in the image. In this work, we generalize the $q$-exponential distribution (with density proportional to) $\exp{(- \half|u|^q)}$ to a stochastic process named \emph{$Q$-exponential (Q-EP) process} that corresponds to the $L_q$ regularization of functions. The key step is to specify consistent multivariate $q$-exponential distributions by choosing from a large family of elliptic contour distributions. The work is closely related to Besov process which is usually defined by the expanded series. Q-EP can be regarded as a definition of Besov process with explicit probabilistic formulation and direct control on the correlation length. From the Bayesian perspective, Q-EP provides a flexible prior on functions with sharper penalty ($q<2$) than the commonly used Gaussian process (GP). We compare GP, Besov and Q-EP in modeling time series and reconstructing images and demonstrate the advantage of the proposed methodology.

Scaling Up Bayesian Uncertainty Quantification for Inverse Problems using Deep Neural Networks

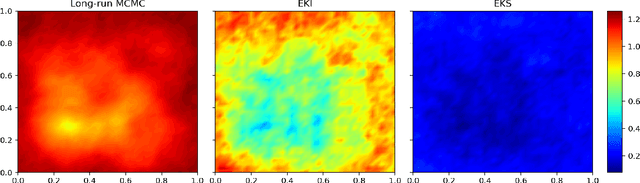
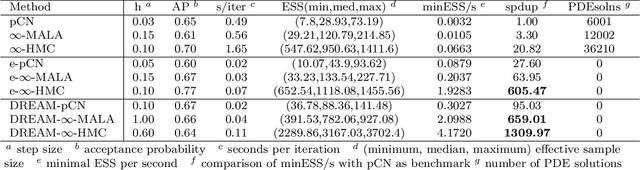
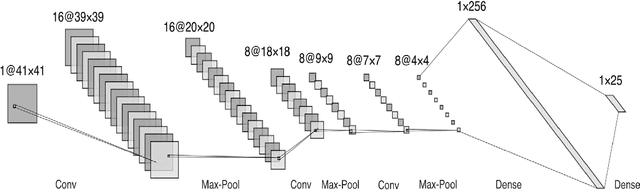
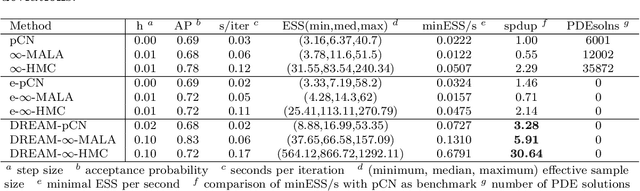
Due to the importance of uncertainty quantification (UQ), Bayesian approach to inverse problems has recently gained popularity in applied mathematics, physics, and engineering. However, traditional Bayesian inference methods based on Markov Chain Monte Carlo (MCMC) tend to be computationally intensive and inefficient for such high dimensional problems. To address this issue, several methods based on surrogate models have been proposed to speed up the inference process. More specifically, the calibration-emulation-sampling (CES) scheme has been proven to be successful in large dimensional UQ problems. In this work, we propose a novel CES approach for Bayesian inference based on deep neural network (DNN) models for the emulation phase. The resulting algorithm is not only computationally more efficient, but also less sensitive to the training set. Further, by using an Autoencoder (AE) for dimension reduction, we have been able to speed up our Bayesian inference method up to three orders of magnitude. Overall, our method, henceforth called \emph{Dimension-Reduced Emulative Autoencoder Monte Carlo (DREAM)} algorithm, is able to scale Bayesian UQ up to thousands of dimensions in physics-constrained inverse problems. Using two low-dimensional (linear and nonlinear) inverse problems we illustrate the validity this approach. Next, we apply our method to two high-dimensional numerical examples (elliptic and advection-diffussion) to demonstrate its computational advantage over existing algorithms.