Deep Q-Exponential Processes

Motivated by deep neural networks, the deep Gaussian process (DGP) generalizes the standard GP by stacking multiple layers of GPs. Despite the enhanced expressiveness, GP, as an $L_2$ regularization prior, tends to be over-smooth and sub-optimal for inhomogeneous subjects, such as images with edges. Recently, Q-exponential process (Q-EP) has been proposed as an $L_q$ relaxation to GP and demonstrated with more desirable regularization properties through a parameter $q>0$ with $q=2$ corresponding to GP. Sharing the similar tractability of posterior and predictive distributions with GP, Q-EP can also be stacked to improve its modeling flexibility. In this paper, we generalize Q-EP to deep Q-EP to enjoy both proper regularization and improved expressiveness. The generalization is realized by introducing shallow Q-EP as a latent variable model and then building a hierarchy of the shallow Q-EP layers. Sparse approximation by inducing points and scalable variational strategy are applied to facilitate the inference. We demonstrate the numerical advantages of the proposed deep Q-EP model by comparing with multiple state-of-the-art deep probabilistic models.

Spatiotemporal Besov Priors for Bayesian Inverse Problems

Fast development in science and technology has driven the need for proper statistical tools to capture special data features such as abrupt changes or sharp contrast. Many applications in the data science seek spatiotemporal reconstruction from a sequence of time-dependent objects with discontinuity or singularity, e.g. dynamic computerized tomography (CT) images with edges. Traditional methods based on Gaussian processes (GP) may not provide satisfactory solutions since they tend to offer over-smooth prior candidates. Recently, Besov process (BP) defined by wavelet expansions with random coefficients has been proposed as a more appropriate prior for this type of Bayesian inverse problems. While BP outperforms GP in imaging analysis to produce edge-preserving reconstructions, it does not automatically incorporate temporal correlation inherited in the dynamically changing images. In this paper, we generalize BP to the spatiotemporal domain (STBP) by replacing the random coefficients in the series expansion with stochastic time functions following Q-exponential process which governs the temporal correlation strength. Mathematical and statistical properties about STBP are carefully studied. A white-noise representation of STBP is also proposed to facilitate the point estimation through maximum a posterior (MAP) and the uncertainty quantification (UQ) by posterior sampling. Two limited-angle CT reconstruction examples and a highly non-linear inverse problem involving Navier-Stokes equation are used to demonstrate the advantage of the proposed STBP in preserving spatial features while accounting for temporal changes compared with the classic STGP and a time-uncorrelated approach.

Bayesian Regularization on Function Spaces via Q-Exponential Process

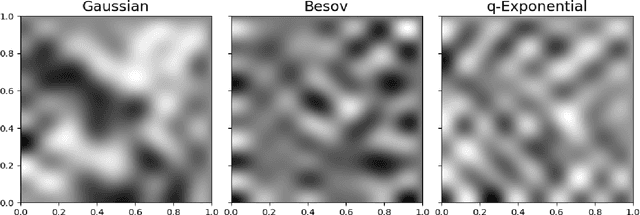
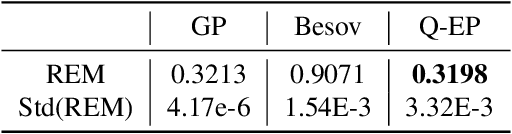
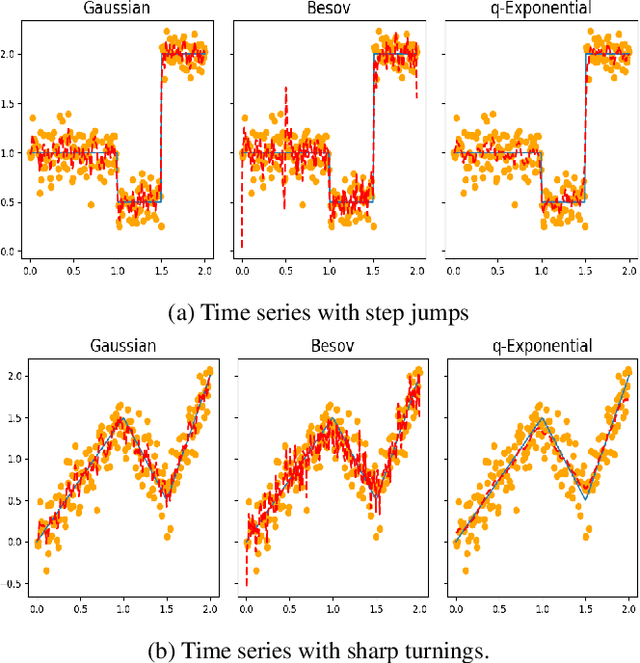
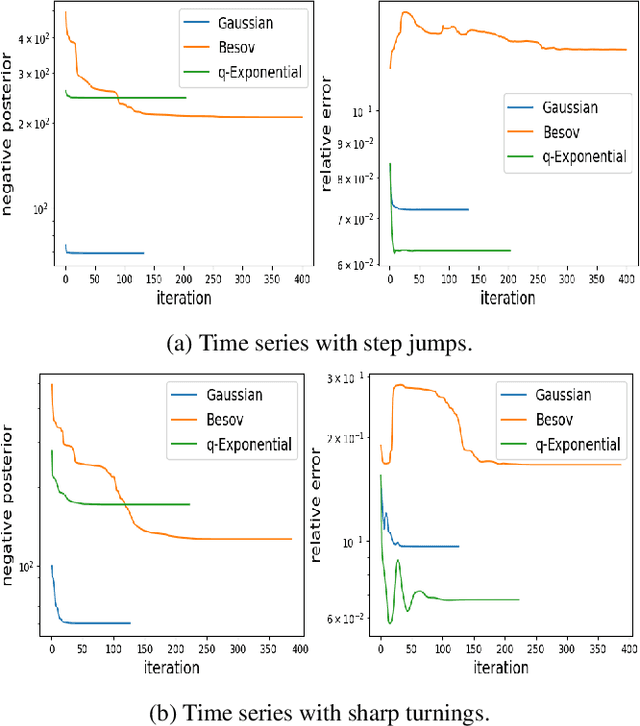
Regularization is one of the most important topics in optimization, statistics and machine learning. To get sparsity in estimating a parameter $u\in\mbR^d$, an $\ell_q$ penalty term, $\Vert u\Vert_q$, is usually added to the objective function. What is the probabilistic distribution corresponding to such $\ell_q$ penalty? What is the correct stochastic process corresponding to $\Vert u\Vert_q$ when we model functions $u\in L^q$? This is important for statistically modeling large dimensional objects, e.g. images, with penalty to preserve certainty properties, e.g. edges in the image. In this work, we generalize the $q$-exponential distribution (with density proportional to) $\exp{(- \half|u|^q)}$ to a stochastic process named \emph{$Q$-exponential (Q-EP) process} that corresponds to the $L_q$ regularization of functions. The key step is to specify consistent multivariate $q$-exponential distributions by choosing from a large family of elliptic contour distributions. The work is closely related to Besov process which is usually defined by the expanded series. Q-EP can be regarded as a definition of Besov process with explicit probabilistic formulation and direct control on the correlation length. From the Bayesian perspective, Q-EP provides a flexible prior on functions with sharper penalty ($q<2$) than the commonly used Gaussian process (GP). We compare GP, Besov and Q-EP in modeling time series and reconstructing images and demonstrate the advantage of the proposed methodology.

Sampling Constrained Continuous Probability Distributions: A Review

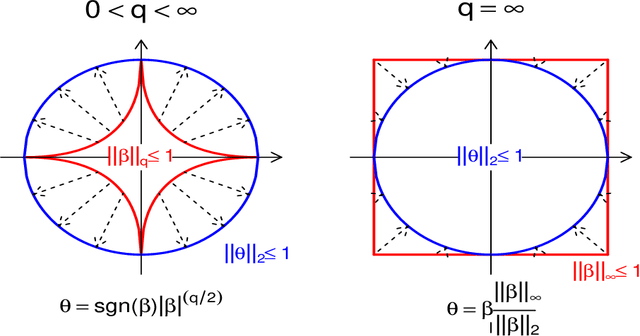
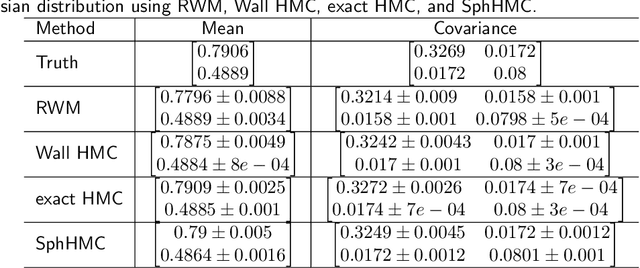
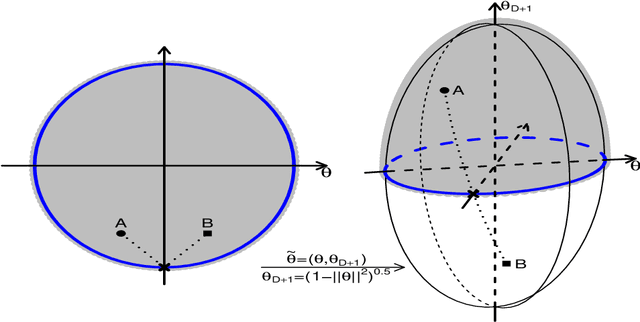
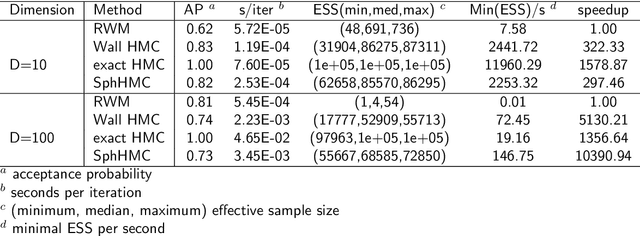
The problem of sampling constrained continuous distributions has frequently appeared in many machine/statistical learning models. Many Monte Carlo Markov Chain (MCMC) sampling methods have been adapted to handle different types of constraints on the random variables. Among these methods, Hamilton Monte Carlo (HMC) and the related approaches have shown significant advantages in terms of computational efficiency compared to other counterparts. In this article, we first review HMC and some extended sampling methods, and then we concretely explain three constrained HMC-based sampling methods, reflection, reformulation, and spherical HMC. For illustration, we apply these methods to solve three well-known constrained sampling problems, truncated multivariate normal distributions, Bayesian regularized regression, and nonparametric density estimation. In this review, we also connect constrained sampling with another similar problem in the statistical design of experiments of constrained design space.

Scaling Up Bayesian Uncertainty Quantification for Inverse Problems using Deep Neural Networks

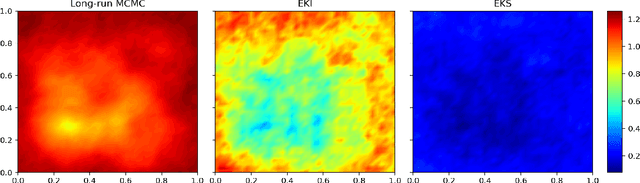
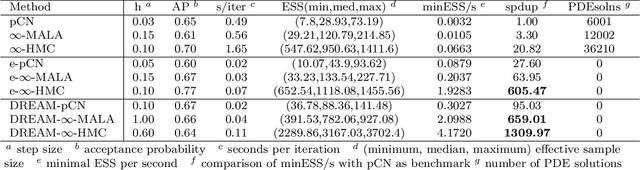
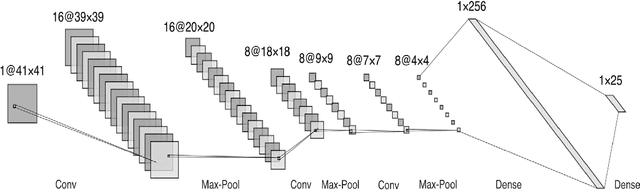
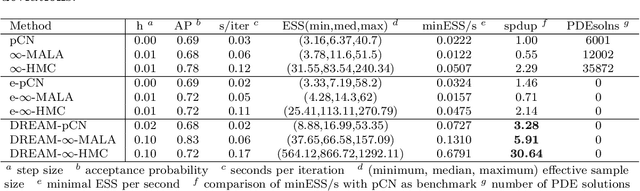
Due to the importance of uncertainty quantification (UQ), Bayesian approach to inverse problems has recently gained popularity in applied mathematics, physics, and engineering. However, traditional Bayesian inference methods based on Markov Chain Monte Carlo (MCMC) tend to be computationally intensive and inefficient for such high dimensional problems. To address this issue, several methods based on surrogate models have been proposed to speed up the inference process. More specifically, the calibration-emulation-sampling (CES) scheme has been proven to be successful in large dimensional UQ problems. In this work, we propose a novel CES approach for Bayesian inference based on deep neural network (DNN) models for the emulation phase. The resulting algorithm is not only computationally more efficient, but also less sensitive to the training set. Further, by using an Autoencoder (AE) for dimension reduction, we have been able to speed up our Bayesian inference method up to three orders of magnitude. Overall, our method, henceforth called \emph{Dimension-Reduced Emulative Autoencoder Monte Carlo (DREAM)} algorithm, is able to scale Bayesian UQ up to thousands of dimensions in physics-constrained inverse problems. Using two low-dimensional (linear and nonlinear) inverse problems we illustrate the validity this approach. Next, we apply our method to two high-dimensional numerical examples (elliptic and advection-diffussion) to demonstrate its computational advantage over existing algorithms.

Sampling constrained probability distributions using Spherical Augmentation

Statistical models with constrained probability distributions are abundant in machine learning. Some examples include regression models with norm constraints (e.g., Lasso), probit, many copula models, and latent Dirichlet allocation (LDA). Bayesian inference involving probability distributions confined to constrained domains could be quite challenging for commonly used sampling algorithms. In this paper, we propose a novel augmentation technique that handles a wide range of constraints by mapping the constrained domain to a sphere in the augmented space. By moving freely on the surface of this sphere, sampling algorithms handle constraints implicitly and generate proposals that remain within boundaries when mapped back to the original space. Our proposed method, called {Spherical Augmentation}, provides a mathematically natural and computationally efficient framework for sampling from constrained probability distributions. We show the advantages of our method over state-of-the-art sampling algorithms, such as exact Hamiltonian Monte Carlo, using several examples including truncated Gaussian distributions, Bayesian Lasso, Bayesian bridge regression, reconstruction of quantized stationary Gaussian process, and LDA for topic modeling.

Split HMC for Gaussian Process Models

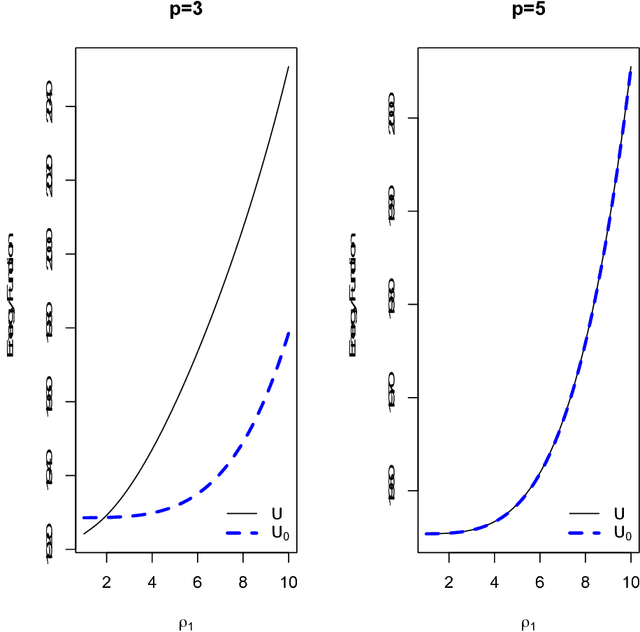
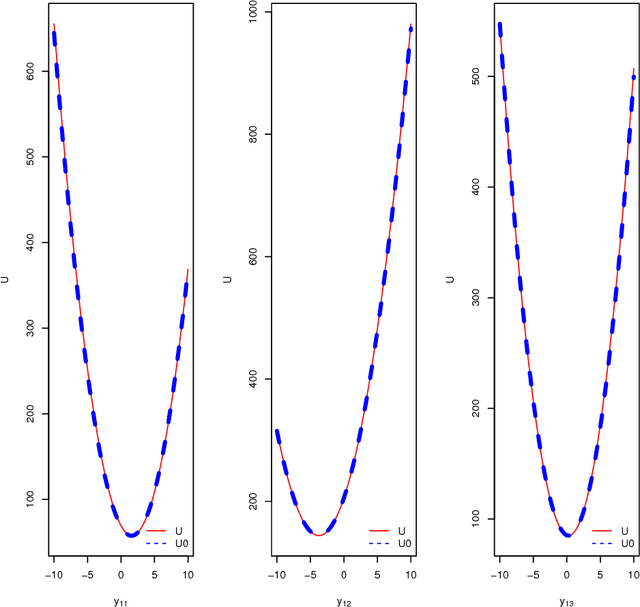
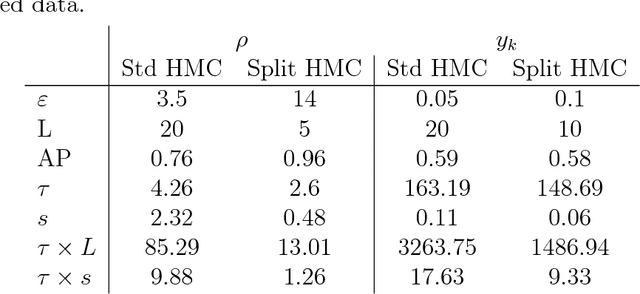
In this paper, we discuss an extension of the Split Hamiltonian Monte Carlo (Split HMC) method for Gaussian process model (GPM). This method is based on splitting the Hamiltonian in a way that allows much of the movement around the state space to be done at low computational cost. To this end, we approximate the negative log density (i.e., the energy function) of the distribution of interest by a quadratic function U0 for which Hamiltonian dynamics can be solved analytically. The overall energy function U is then written as U0 + U1, where U1 is the approximation error. The Hamiltonian is then split into two parts; one part is based on U0 is handled analytically, the other part is based on U1 for which we approximate Hamiltonian's equations by discretizing time. We use simulated and real data to compare the performance of our method to the standard HMC. We find that splitting the Hamiltonian for GP models could lead to substantial improvement (up to 10 folds) of sampling efficiency, which is measured in terms of the amount of time required for producing an independent sample with high acceptance probability from posterior distributions.