Active Learning for Manifold Gaussian Process Regression

This paper introduces an active learning framework for manifold Gaussian Process (GP) regression, combining manifold learning with strategic data selection to improve accuracy in high-dimensional spaces. Our method jointly optimizes a neural network for dimensionality reduction and a Gaussian process regressor in the latent space, supervised by an active learning criterion that minimizes global prediction error. Experiments on synthetic data demonstrate superior performance over randomly sequential learning. The framework efficiently handles complex, discontinuous functions while preserving computational tractability, offering practical value for scientific and engineering applications. Future work will focus on scalability and uncertainty-aware manifold learning.

Accelerating Particle-based Energetic Variational Inference

In this work, we propose a novel particle-based variational inference (ParVI) method that accelerates the EVI-Im. Inspired by energy quadratization (EQ) and operator splitting techniques for gradient flows, our approach efficiently drives particles towards the target distribution. Unlike EVI-Im, which employs the implicit Euler method to solve variational-preserving particle dynamics for minimizing the KL divergence, derived using a "discretize-then-variational" approach, the proposed algorithm avoids repeated evaluation of inter-particle interaction terms, significantly reducing computational cost. The framework is also extensible to other gradient-based sampling techniques. Through several numerical experiments, we demonstrate that our method outperforms existing ParVI approaches in efficiency, robustness, and accuracy.

Optimal Kernel Learning for Gaussian Process Models with High-Dimensional Input

Gaussian process (GP) regression is a popular surrogate modeling tool for computer simulations in engineering and scientific domains. However, it often struggles with high computational costs and low prediction accuracy when the simulation involves too many input variables. For some simulation models, the outputs may only be significantly influenced by a small subset of the input variables, referred to as the ``active variables''. We propose an optimal kernel learning approach to identify these active variables, thereby overcoming GP model limitations and enhancing system understanding. Our method approximates the original GP model's covariance function through a convex combination of kernel functions, each utilizing low-dimensional subsets of input variables. Inspired by the Fedorov-Wynn algorithm from optimal design literature, we develop an optimal kernel learning algorithm to determine this approximation. We incorporate the effect heredity principle, a concept borrowed from the field of ``design and analysis of experiments'', to ensure sparsity in active variable selection. Through several examples, we demonstrate that the proposed method outperforms alternative approaches in correctly identifying active input variables and improving prediction accuracy. It is an effective solution for interpreting the surrogate GP regression and simplifying the complex underlying system.

Fair Multivariate Adaptive Regression Splines for Ensuring Equity and Transparency

Predictive analytics is widely used in various domains, including education, to inform decision-making and improve outcomes. However, many predictive models are proprietary and inaccessible for evaluation or modification by researchers and practitioners, limiting their accountability and ethical design. Moreover, predictive models are often opaque and incomprehensible to the officials who use them, reducing their trust and utility. Furthermore, predictive models may introduce or exacerbate bias and inequity, as they have done in many sectors of society. Therefore, there is a need for transparent, interpretable, and fair predictive models that can be easily adopted and adapted by different stakeholders. In this paper, we propose a fair predictive model based on multivariate adaptive regression splines(MARS) that incorporates fairness measures in the learning process. MARS is a non-parametric regression model that performs feature selection, handles non-linear relationships, generates interpretable decision rules, and derives optimal splitting criteria on the variables. Specifically, we integrate fairness into the knot optimization algorithm and provide theoretical and empirical evidence of how it results in a fair knot placement. We apply our fairMARS model to real-world data and demonstrate its effectiveness in terms of accuracy and equity. Our paper contributes to the advancement of responsible and ethical predictive analytics for social good.

Learned Mappings for Targeted Free Energy Perturbation between Peptide Conformations

Targeted free energy perturbation uses an invertible mapping to promote configuration space overlap and the convergence of free energy estimates. However, developing suitable mappings can be challenging. Wirnsberger et al. (2020) demonstrated the use of machine learning to train deep neural networks that map between Boltzmann distributions for different thermodynamic states. Here, we adapt their approach to free energy differences of a flexible bonded molecule, deca-alanine, with harmonic biases with different spring centers. When the neural network is trained until ``early stopping'' - when the loss value of the test set increases - we calculate accurate free energy differences between thermodynamic states with spring centers separated by 1 \r{A} and sometimes 2 \r{A}. For more distant thermodynamic states, the mapping does not produce structures representative of the target state and the method does not reproduce reference calculations.

Sampling Constrained Continuous Probability Distributions: A Review

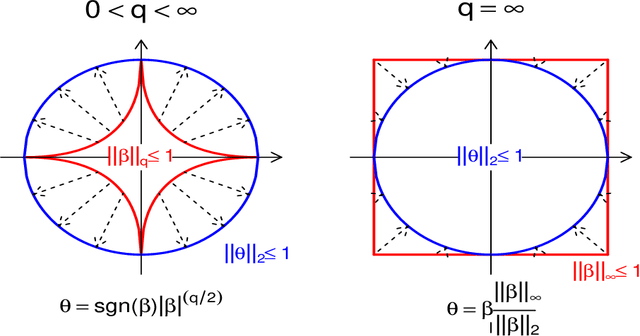
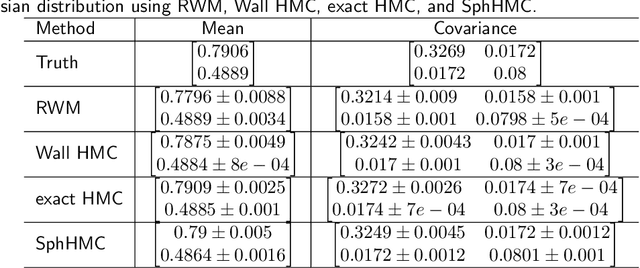
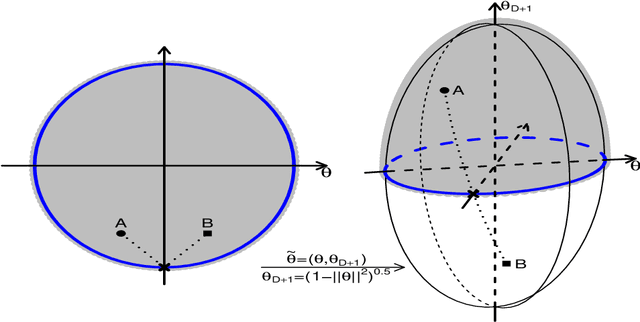
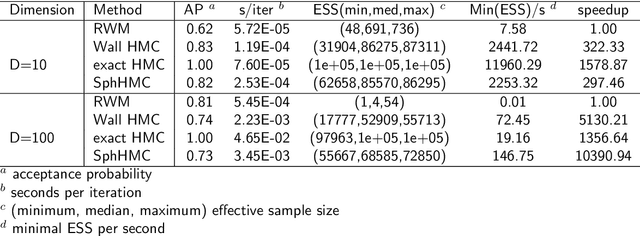
The problem of sampling constrained continuous distributions has frequently appeared in many machine/statistical learning models. Many Monte Carlo Markov Chain (MCMC) sampling methods have been adapted to handle different types of constraints on the random variables. Among these methods, Hamilton Monte Carlo (HMC) and the related approaches have shown significant advantages in terms of computational efficiency compared to other counterparts. In this article, we first review HMC and some extended sampling methods, and then we concretely explain three constrained HMC-based sampling methods, reflection, reformulation, and spherical HMC. For illustration, we apply these methods to solve three well-known constrained sampling problems, truncated multivariate normal distributions, Bayesian regularized regression, and nonparametric density estimation. In this review, we also connect constrained sampling with another similar problem in the statistical design of experiments of constrained design space.

Low-Discrepancy Points via Energetic Variational Inference

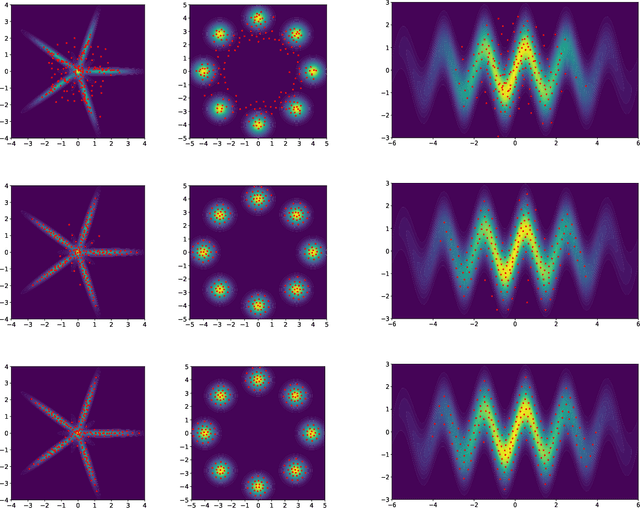
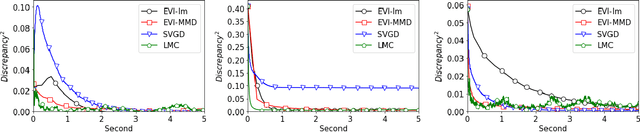
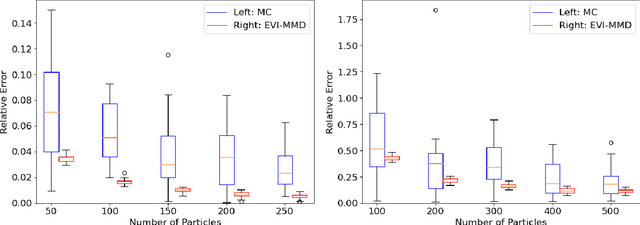
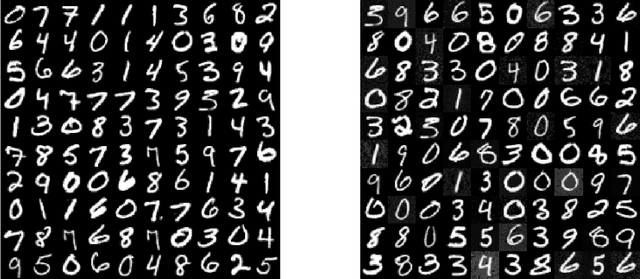
In this paper, we propose a deterministic variational inference approach and generate low-discrepancy points by minimizing the kernel discrepancy, also known as the Maximum Mean Discrepancy or MMD. Based on the general energetic variational inference framework by Wang et. al. (2021), minimizing the kernel discrepancy is transformed to solving a dynamic ODE system via the explicit Euler scheme. We name the resulting algorithm EVI-MMD and demonstrate it through examples in which the target distribution is fully specified, partially specified up to the normalizing constant, and empirically known in the form of training data. Its performances are satisfactory compared to alternative methods in the applications of distribution approximation, numerical integration, and generative learning. The EVI-MMD algorithm overcomes the bottleneck of the existing MMD-descent algorithms, which are mostly applicable to two-sample problems. Algorithms with more sophisticated structures and potential advantages can be developed under the EVI framework.

Particle-based Energetic Variational Inference

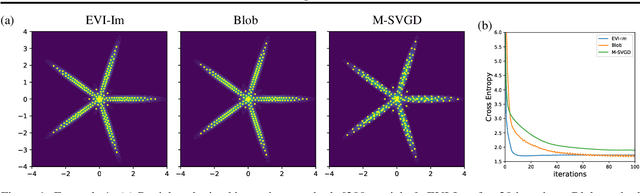
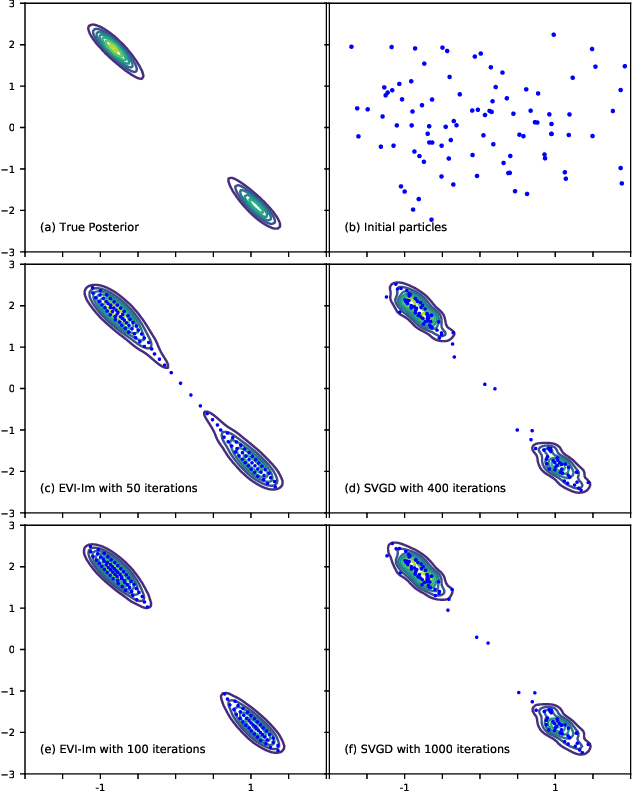
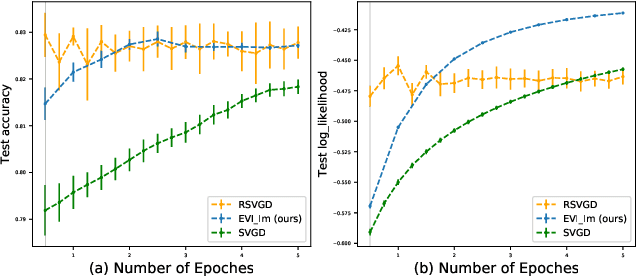
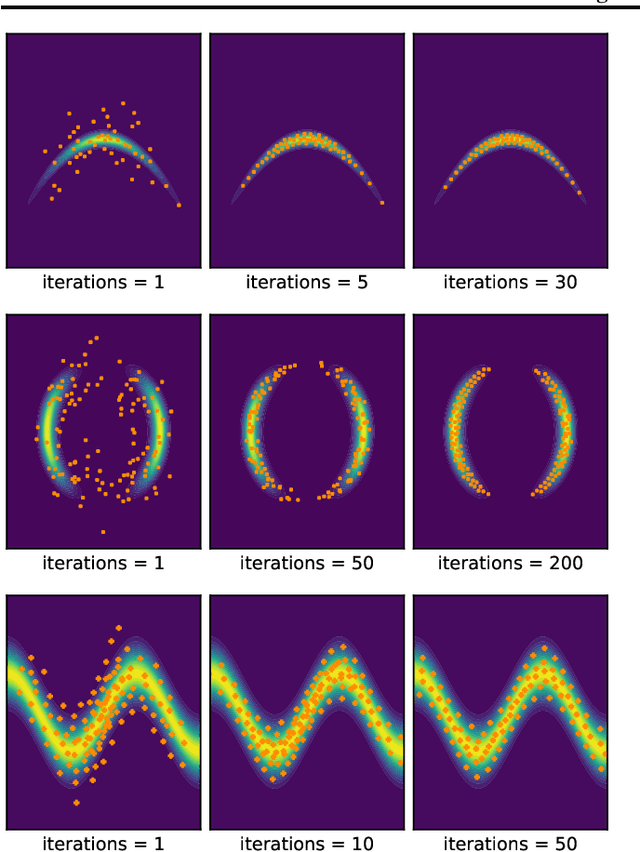
We introduce a new variational inference framework, called energetic variational inference (EVI). The novelty of the EVI lies in the new mechanism of minimizing the KL-divergence, or other variational object functions, which is based on the energy-dissipation law. Under the EVI framework, we can derive many existing particle-based variational inference (ParVI) methods, such as the classic Stein variational gradient descent (SVGD), as special schemes of the EVI with particle approximation to the probability density. More importantly, many new variational inference schemes can be developed under this framework. In this paper, we propose one such particle-based EVI scheme, which performs the particle-based approximation of the density first and then uses the approximated density in the variational procedure. Thanks to this Approximation-then-Variation order, the new scheme can maintain the variational structure at the particle level, which enables us to design an algorithm that can significantly decrease the KL- divergence in every iteration. Numerical experiments show the proposed method outperforms some existing ParVI methods in terms of fidelity to the target distribution.