Sampling Constrained Continuous Probability Distributions: A Review
Paper and Code
Sep 26, 2022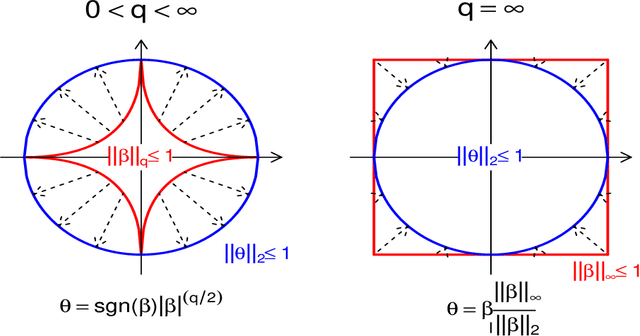
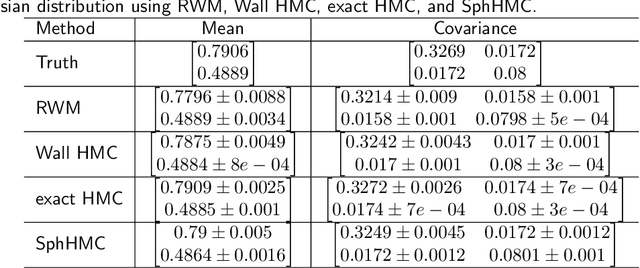
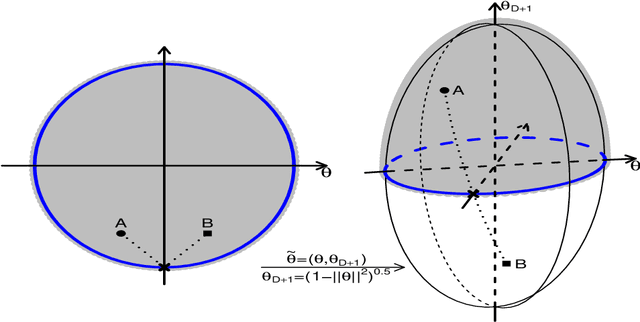
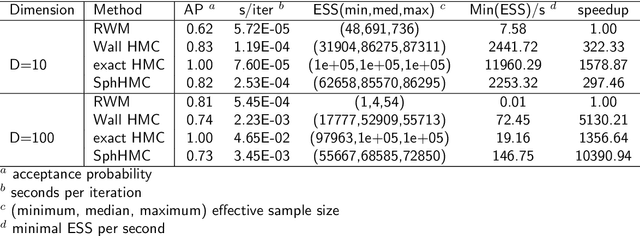
The problem of sampling constrained continuous distributions has frequently appeared in many machine/statistical learning models. Many Monte Carlo Markov Chain (MCMC) sampling methods have been adapted to handle different types of constraints on the random variables. Among these methods, Hamilton Monte Carlo (HMC) and the related approaches have shown significant advantages in terms of computational efficiency compared to other counterparts. In this article, we first review HMC and some extended sampling methods, and then we concretely explain three constrained HMC-based sampling methods, reflection, reformulation, and spherical HMC. For illustration, we apply these methods to solve three well-known constrained sampling problems, truncated multivariate normal distributions, Bayesian regularized regression, and nonparametric density estimation. In this review, we also connect constrained sampling with another similar problem in the statistical design of experiments of constrained design space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge