Particle-based Energetic Variational Inference

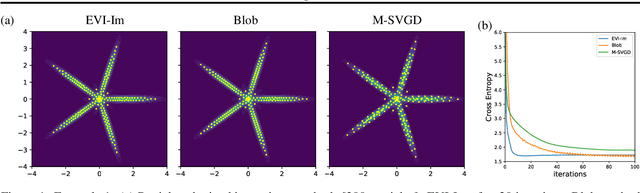
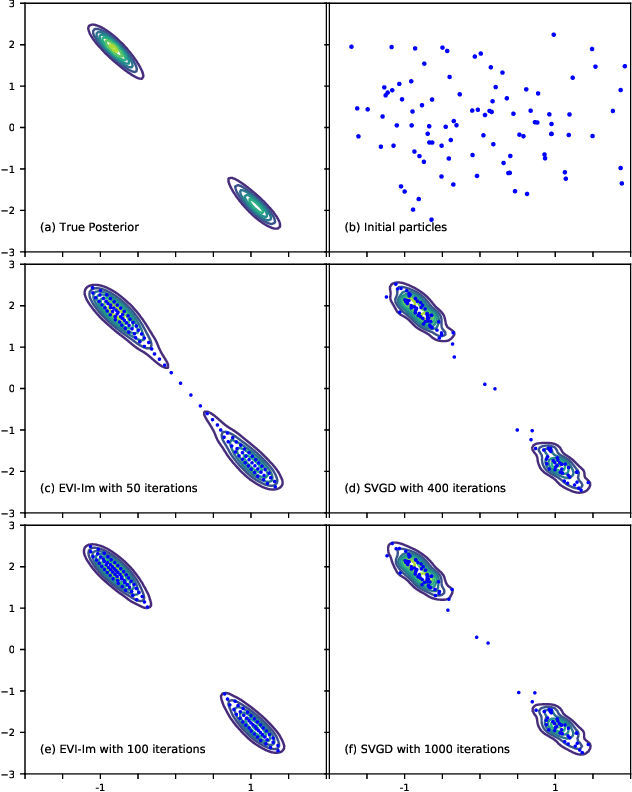
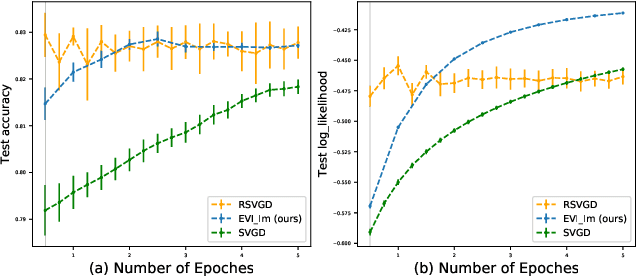
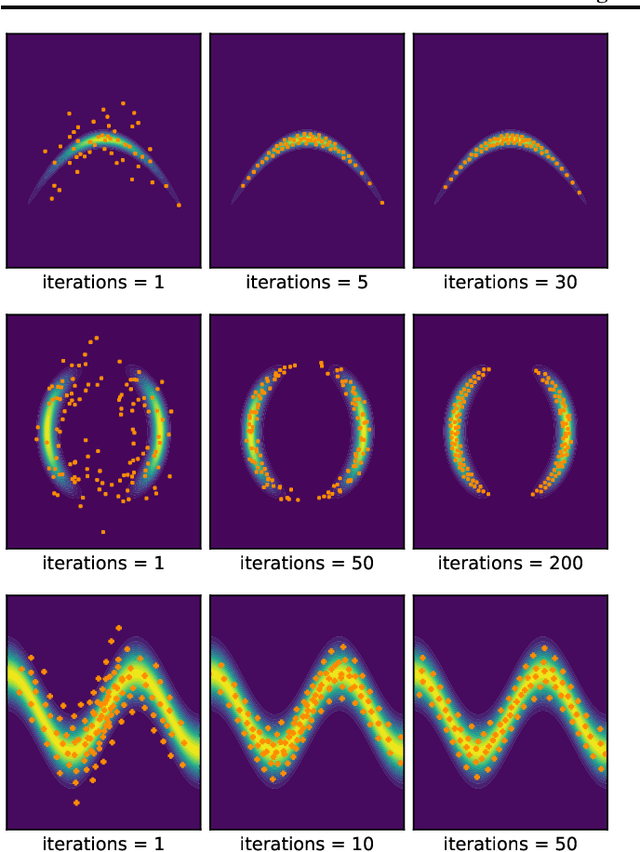
We introduce a new variational inference framework, called energetic variational inference (EVI). The novelty of the EVI lies in the new mechanism of minimizing the KL-divergence, or other variational object functions, which is based on the energy-dissipation law. Under the EVI framework, we can derive many existing particle-based variational inference (ParVI) methods, such as the classic Stein variational gradient descent (SVGD), as special schemes of the EVI with particle approximation to the probability density. More importantly, many new variational inference schemes can be developed under this framework. In this paper, we propose one such particle-based EVI scheme, which performs the particle-based approximation of the density first and then uses the approximated density in the variational procedure. Thanks to this Approximation-then-Variation order, the new scheme can maintain the variational structure at the particle level, which enables us to design an algorithm that can significantly decrease the KL- divergence in every iteration. Numerical experiments show the proposed method outperforms some existing ParVI methods in terms of fidelity to the target distribution.