Split HMC for Gaussian Process Models
Paper and Code
Jul 14, 2012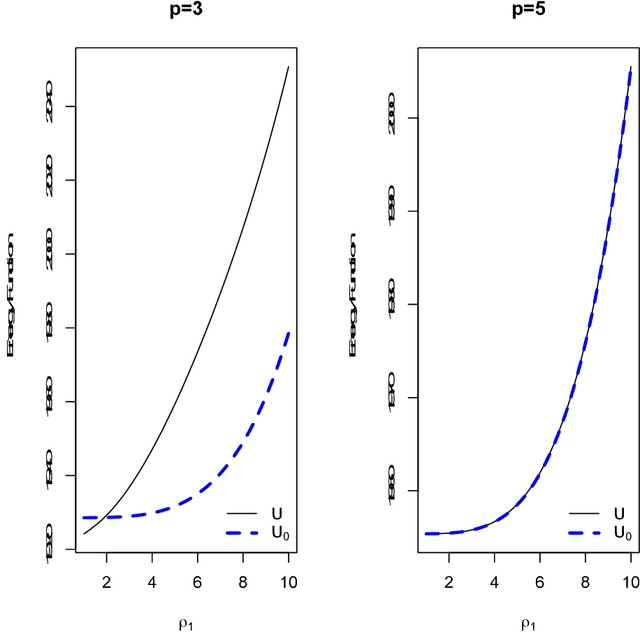

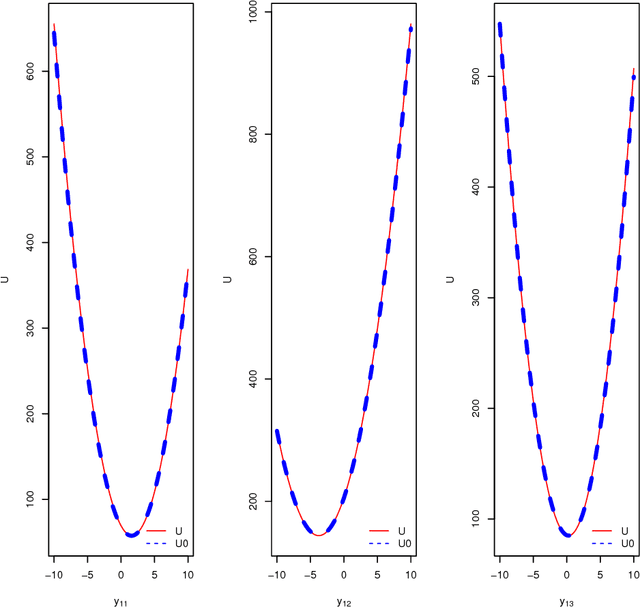
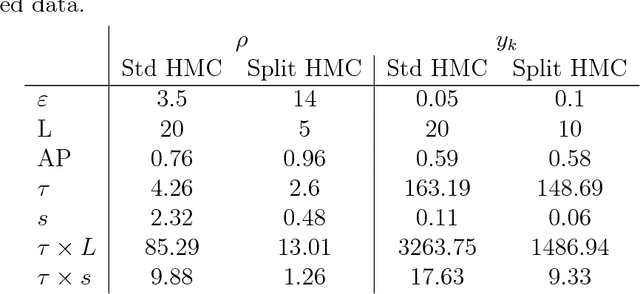
In this paper, we discuss an extension of the Split Hamiltonian Monte Carlo (Split HMC) method for Gaussian process model (GPM). This method is based on splitting the Hamiltonian in a way that allows much of the movement around the state space to be done at low computational cost. To this end, we approximate the negative log density (i.e., the energy function) of the distribution of interest by a quadratic function U0 for which Hamiltonian dynamics can be solved analytically. The overall energy function U is then written as U0 + U1, where U1 is the approximation error. The Hamiltonian is then split into two parts; one part is based on U0 is handled analytically, the other part is based on U1 for which we approximate Hamiltonian's equations by discretizing time. We use simulated and real data to compare the performance of our method to the standard HMC. We find that splitting the Hamiltonian for GP models could lead to substantial improvement (up to 10 folds) of sampling efficiency, which is measured in terms of the amount of time required for producing an independent sample with high acceptance probability from posterior distributions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge