Continual Test-Time Adaptation for Single Image Defocus Deblurring via Causal Siamese Networks

Single image defocus deblurring (SIDD) aims to restore an all-in-focus image from a defocused one. Distribution shifts in defocused images generally lead to performance degradation of existing methods during out-of-distribution inferences. In this work, we gauge the intrinsic reason behind the performance degradation, which is identified as the heterogeneity of lens-specific point spread functions. Empirical evidence supports this finding, motivating us to employ a continual test-time adaptation (CTTA) paradigm for SIDD. However, traditional CTTA methods, which primarily rely on entropy minimization, cannot sufficiently explore task-dependent information for pixel-level regression tasks like SIDD. To address this issue, we propose a novel Siamese networks-based continual test-time adaptation framework, which adapts source models to continuously changing target domains only requiring unlabeled target data in an online manner. To further mitigate semantically erroneous textures introduced by source SIDD models under severe degradation, we revisit the learning paradigm through a structural causal model and propose Causal Siamese networks (CauSiam). Our method leverages large-scale pre-trained vision-language models to derive discriminative universal semantic priors and integrates these priors into Siamese networks, ensuring causal identifiability between blurry inputs and restored images. Extensive experiments demonstrate that CauSiam effectively improves the generalization performance of existing SIDD methods in continuously changing domains.

Practical Parallel Algorithms for Non-Monotone Submodular Maximization

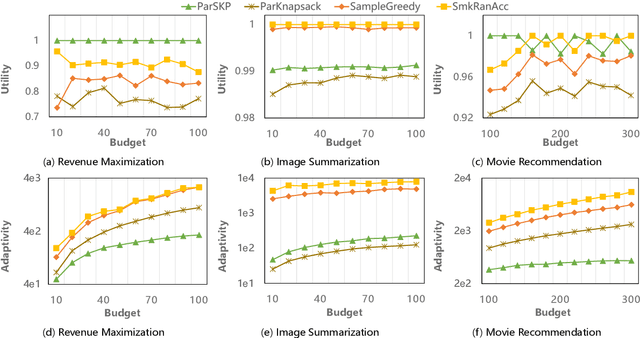
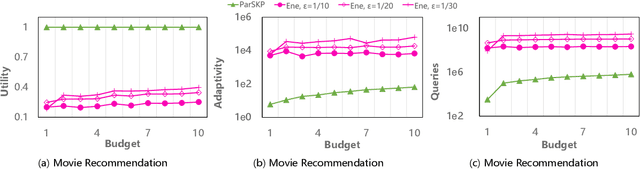
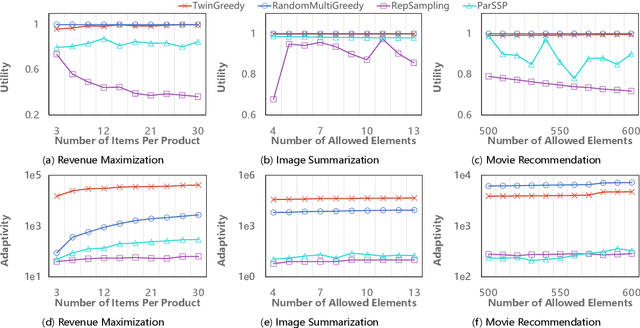
Submodular maximization has found extensive applications in various domains within the field of artificial intelligence, including but not limited to machine learning, computer vision, and natural language processing. With the increasing size of datasets in these domains, there is a pressing need to develop efficient and parallelizable algorithms for submodular maximization. One measure of the parallelizability of a submodular maximization algorithm is its adaptive complexity, which indicates the number of sequential rounds where a polynomial number of queries to the objective function can be executed in parallel. In this paper, we study the problem of non-monotone submodular maximization subject to a knapsack constraint, and propose the first combinatorial algorithm achieving an $(8+\epsilon)$-approximation under $\mathcal{O}(\log n)$ adaptive complexity, which is \textit{optimal} up to a factor of $\mathcal{O}(\log\log n)$. Moreover, we also propose the first algorithm with both provable approximation ratio and sublinear adaptive complexity for the problem of non-monotone submodular maximization subject to a $k$-system constraint. As a by-product, we show that our two algorithms can also be applied to the special case of submodular maximization subject to a cardinality constraint, and achieve performance bounds comparable with those of state-of-the-art algorithms. Finally, the effectiveness of our approach is demonstrated by extensive experiments on real-world applications.

Neural Invertible Variable-degree Optical Aberrations Correction

Optical aberrations of optical systems cause significant degradation of imaging quality. Aberration correction by sophisticated lens designs and special glass materials generally incurs high cost of manufacturing and the increase in the weight of optical systems, thus recent work has shifted to aberration correction with deep learning-based post-processing. Though real-world optical aberrations vary in degree, existing methods cannot eliminate variable-degree aberrations well, especially for the severe degrees of degradation. Also, previous methods use a single feed-forward neural network and suffer from information loss in the output. To address the issues, we propose a novel aberration correction method with an invertible architecture by leveraging its information-lossless property. Within the architecture, we develop conditional invertible blocks to allow the processing of aberrations with variable degrees. Our method is evaluated on both a synthetic dataset from physics-based imaging simulation and a real captured dataset. Quantitative and qualitative experimental results demonstrate that our method outperforms compared methods in correcting variable-degree optical aberrations.

Deterministic Approximation for Submodular Maximization over a Matroid in Nearly Linear Time

We study the problem of maximizing a non-monotone, non-negative submodular function subject to a matroid constraint. The prior best-known deterministic approximation ratio for this problem is $\frac{1}{4}-\epsilon$ under $\mathcal{O}(({n^4}/{\epsilon})\log n)$ time complexity. We show that this deterministic ratio can be improved to $\frac{1}{4}$ under $\mathcal{O}(nr)$ time complexity, and then present a more practical algorithm dubbed TwinGreedyFast which achieves $\frac{1}{4}-\epsilon$ deterministic ratio in nearly-linear running time of $\mathcal{O}(\frac{n}{\epsilon}\log\frac{r}{\epsilon})$. Our approach is based on a novel algorithmic framework of simultaneously constructing two candidate solution sets through greedy search, which enables us to get improved performance bounds by fully exploiting the properties of independence systems. As a byproduct of this framework, we also show that TwinGreedyFast achieves $\frac{1}{2p+2}-\epsilon$ deterministic ratio under a $p$-set system constraint with the same time complexity. To showcase the practicality of our approach, we empirically evaluated the performance of TwinGreedyFast on two network applications, and observed that it outperforms the state-of-the-art deterministic and randomized algorithms with efficient implementations for our problem.

Super Resolution for Root Imaging

High-resolution cameras have become very helpful for plant phenotyping by providing a mechanism for tasks such as target versus background discrimination, and the measurement and analysis of fine-above-ground plant attributes, e.g., the venation network of leaves. However, the acquisition of high-resolution (HR) imagery of roots in situ remains a challenge. We apply super-resolution (SR) convolutional neural networks (CNNs) to boost the resolution capability of a backscatter X-ray system designed to image buried roots. To overcome limited available backscatter X-ray data for training, we compare three alternatives for training: i) non-plant-root images, ii) plant-root images, and iii) pretraining the model with non-plant-root images and fine-tuning with plant-root images and two deep learning approaches i) Fast Super Resolution Convolutional Neural Network and ii) Super Resolution Generative Adversarial Network). We evaluate SR performance using signal to noise ratio (SNR) and intersection over union (IoU) metrics when segmenting the SR images. In our experiments, we observe that the studied SR models improve the quality of the low-resolution images (LR) of plant roots of an unseen dataset in terms of SNR. Likewise, we demonstrate that SR pre-processing boosts the performance of a machine learning system trained to separate plant roots from their background. In addition, we show examples of backscatter X-ray images upscaled by using the SR model. The current technology for non-intrusive root imaging acquires noisy and LR images. In this study, we show that this issue can be tackled by the incorporation of a deep-learning based SR model in the image formation process.