Practical Parallel Algorithms for Non-Monotone Submodular Maximization
Paper and Code
Aug 21, 2023
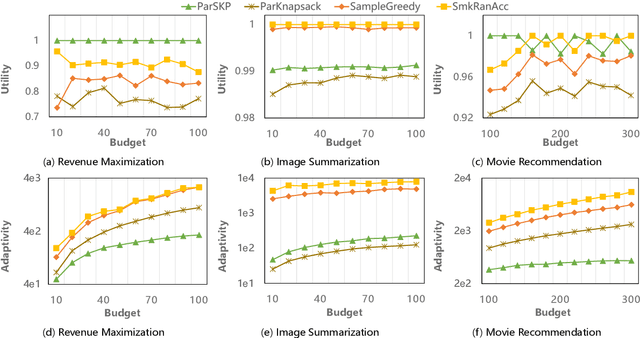
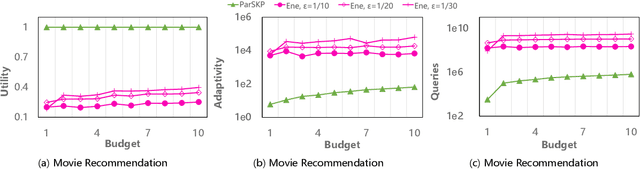
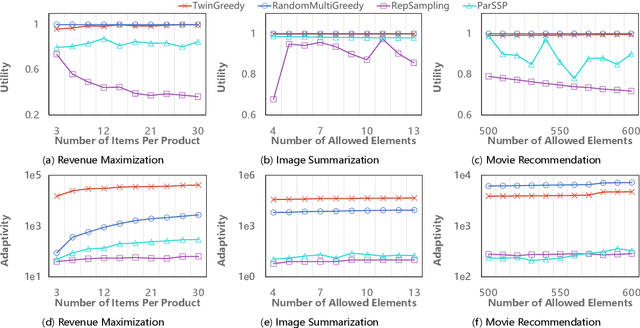
Submodular maximization has found extensive applications in various domains within the field of artificial intelligence, including but not limited to machine learning, computer vision, and natural language processing. With the increasing size of datasets in these domains, there is a pressing need to develop efficient and parallelizable algorithms for submodular maximization. One measure of the parallelizability of a submodular maximization algorithm is its adaptive complexity, which indicates the number of sequential rounds where a polynomial number of queries to the objective function can be executed in parallel. In this paper, we study the problem of non-monotone submodular maximization subject to a knapsack constraint, and propose the first combinatorial algorithm achieving an $(8+\epsilon)$-approximation under $\mathcal{O}(\log n)$ adaptive complexity, which is \textit{optimal} up to a factor of $\mathcal{O}(\log\log n)$. Moreover, we also propose the first algorithm with both provable approximation ratio and sublinear adaptive complexity for the problem of non-monotone submodular maximization subject to a $k$-system constraint. As a by-product, we show that our two algorithms can also be applied to the special case of submodular maximization subject to a cardinality constraint, and achieve performance bounds comparable with those of state-of-the-art algorithms. Finally, the effectiveness of our approach is demonstrated by extensive experiments on real-world applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge