Post-Decision State-Based Online Learning for Delay-Energy-Aware Flow Allocation in Wireless Systems

We develop a structure-aware reinforcement learning (RL) approach for delay- and energy-aware flow allocation in 5G User Plane Functions (UPFs). We consider a dynamic system with $K$ heterogeneous UPFs of varying capacities that handle stochastic arrivals of $M$ flow types, each with distinct rate requirements. We model the system as a Markov decision process (MDP) to capture the stochastic nature of flow arrivals and departures (possibly unknown), as well as the impact of flow allocation in the system. To solve this problem, we propose a post-decision state (PDS) based value iteration algorithm that exploits the underlying structure of the MDP. By separating action-controlled dynamics from exogenous factors, PDS enables faster convergence and efficient adaptive flow allocation, even in the absence of statistical knowledge about exogenous variables. Simulation results demonstrate that the proposed method converges faster and achieves lower long-term cost than standard Q-learning, highlighting the effectiveness of PDS-based RL for resource allocation in wireless networks.

Diffusion-based Decentralized Federated Multi-Task Representation Learning

Representation learning is a widely adopted framework for learning in data-scarce environments to obtain a feature extractor or representation from various different yet related tasks. Despite extensive research on representation learning, decentralized approaches remain relatively underexplored. This work develops a decentralized projected gradient descent-based algorithm for multi-task representation learning. We focus on the problem of multi-task linear regression in which multiple linear regression models share a common, low-dimensional linear representation. We present an alternating projected gradient descent and minimization algorithm for recovering a low-rank feature matrix in a diffusion-based decentralized and federated fashion. We obtain constructive, provable guarantees that provide a lower bound on the required sample complexity and an upper bound on the iteration complexity of our proposed algorithm. We analyze the time and communication complexity of our algorithm and show that it is fast and communication-efficient. We performed numerical simulations to validate the performance of our algorithm and compared it with benchmark algorithms.

Beyond Centralization: Provable Communication Efficient Decentralized Multi-Task Learning

Representation learning is a widely adopted framework for learning in data-scarce environments, aiming to extract common features from related tasks. While centralized approaches have been extensively studied, decentralized methods remain largely underexplored. We study decentralized multi-task representation learning in which the features share a low-rank structure. We consider multiple tasks, each with a finite number of data samples, where the observations follow a linear model with task-specific parameters. In the decentralized setting, task data are distributed across multiple nodes, and information exchange between nodes is constrained by a communication network. The goal is to recover the underlying feature matrix whose rank is much smaller than both the parameter dimension and the number of tasks. We propose a new alternating projected gradient and minimization algorithm with provable accuracy guarantees. We provide comprehensive characterizations of the time, communication, and sample complexities. Importantly, the communication complexity is independent of the target accuracy, which significantly reduces communication cost compared to prior methods. Numerical simulations validate the theoretical analysis across different dimensions and network topologies, and demonstrate regimes in which decentralized learning outperforms centralized federated approaches.

Neural Contextual Bandits Under Delayed Feedback Constraints

This paper presents a new algorithm for neural contextual bandits (CBs) that addresses the challenge of delayed reward feedback, where the reward for a chosen action is revealed after a random, unknown delay. This scenario is common in applications such as online recommendation systems and clinical trials, where reward feedback is delayed because the outcomes or results of a user's actions (such as recommendations or treatment responses) take time to manifest and be measured. The proposed algorithm, called Delayed NeuralUCB, uses an upper confidence bound (UCB)-based exploration strategy. Under the assumption of independent and identically distributed sub-exponential reward delays, we derive an upper bound on the cumulative regret over a T-length horizon. We further consider a variant of the algorithm, called Delayed NeuralTS, that uses Thompson Sampling-based exploration. Numerical experiments on real-world datasets, such as MNIST and Mushroom, along with comparisons to benchmark approaches, demonstrate that the proposed algorithms effectively manage varying delays and are well-suited for complex real-world scenarios.

Byzantine Resilient Federated Multi-Task Representation Learning

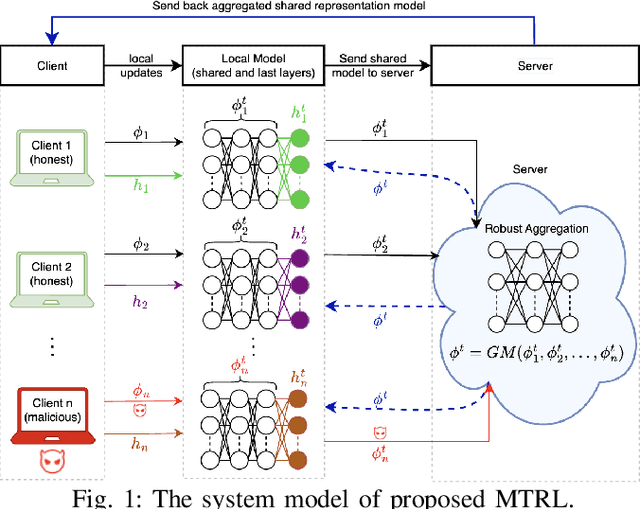
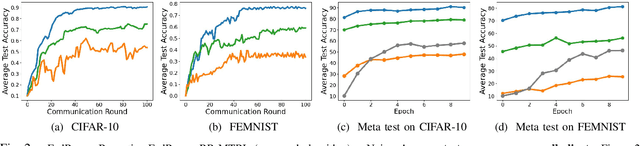
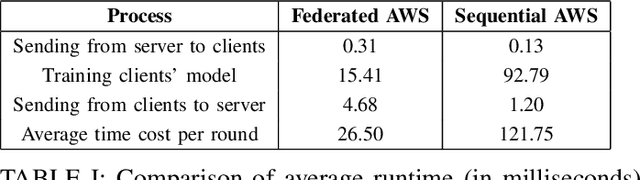
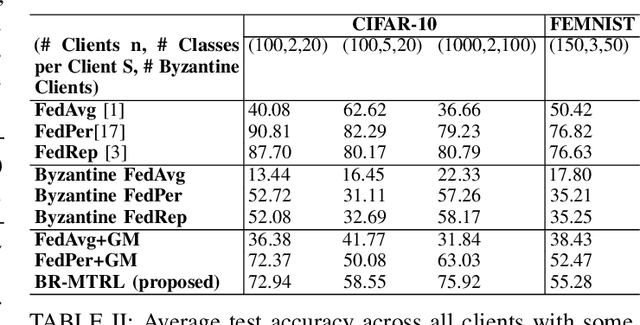
In this paper, we propose BR-MTRL, a Byzantine-resilient multi-task representation learning framework that handles faulty or malicious agents. Our approach leverages representation learning through a shared neural network model, where all clients share fixed layers, except for a client-specific final layer. This structure captures shared features among clients while enabling individual adaptation, making it a promising approach for leveraging client data and computational power in heterogeneous federated settings to learn personalized models. To learn the model, we employ an alternating gradient descent strategy: each client optimizes its local model, updates its final layer, and sends estimates of the shared representation to a central server for aggregation. To defend against Byzantine agents, we employ geometric median aggregation for robust client-server communication. Our method enables personalized learning while maintaining resilience in distributed settings. We implemented the proposed alternating gradient descent algorithm in a federated testbed built using Amazon Web Services (AWS) platform and compared its performance with various benchmark algorithms and their variations. Through extensive experiments using real-world datasets, including CIFAR-10 and FEMINIST, we demonstrated the effectiveness and robustness of our approach and its transferability to new unseen clients with limited data, even in the presence of Byzantine adversaries.

Fast and Sample Efficient Multi-Task Representation Learning in Stochastic Contextual Bandits

We study how representation learning can improve the learning efficiency of contextual bandit problems. We study the setting where we play T contextual linear bandits with dimension d simultaneously, and these T bandit tasks collectively share a common linear representation with a dimensionality of r much smaller than d. We present a new algorithm based on alternating projected gradient descent (GD) and minimization estimator to recover a low-rank feature matrix. Using the proposed estimator, we present a multi-task learning algorithm for linear contextual bandits and prove the regret bound of our algorithm. We presented experiments and compared the performance of our algorithm against benchmark algorithms.

Distributed Multi-Task Learning for Stochastic Bandits with Context Distribution and Stage-wise Constraints

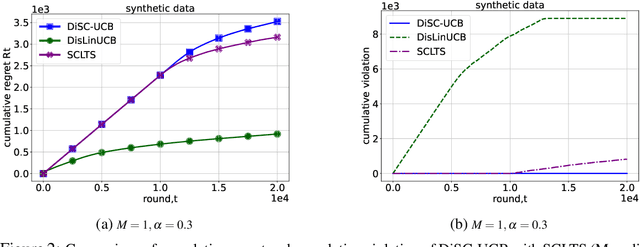
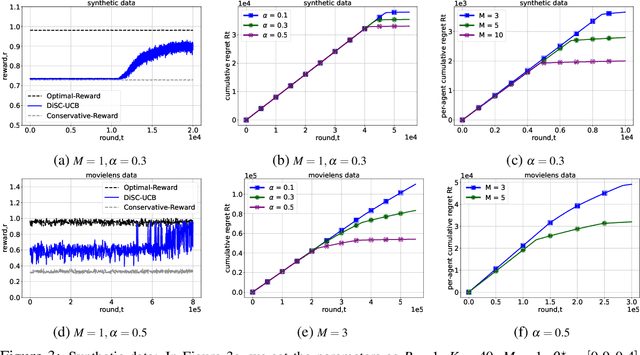
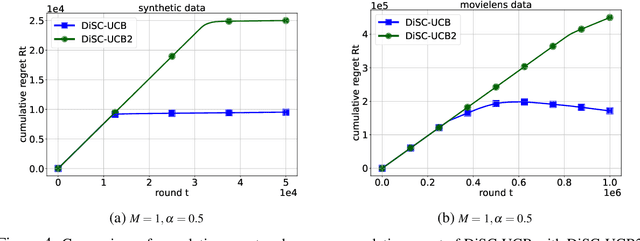
We present the problem of conservative distributed multi-task learning in stochastic linear contextual bandits with heterogeneous agents. This extends conservative linear bandits to a distributed setting where M agents tackle different but related tasks while adhering to stage-wise performance constraints. The exact context is unknown, and only a context distribution is available to the agents as in many practical applications that involve a prediction mechanism to infer context, such as stock market prediction and weather forecast. We propose a distributed upper confidence bound (UCB) algorithm, DiSC-UCB. Our algorithm constructs a pruned action set during each round to ensure the constraints are met. Additionally, it includes synchronized sharing of estimates among agents via a central server using well-structured synchronization steps. We prove the regret and communication bounds on the algorithm. We extend the problem to a setting where the agents are unaware of the baseline reward. For this setting, we provide a modified algorithm, DiSC-UCB2, and we show that the modified algorithm achieves the same regret and communication bounds. We empirically validated the performance of our algorithm on synthetic data and real-world Movielens-100K data.

Thompson Sampling for Stochastic Bandits with Noisy Contexts: An Information-Theoretic Regret Analysis

We explore a stochastic contextual linear bandit problem where the agent observes a noisy, corrupted version of the true context through a noise channel with an unknown noise parameter. Our objective is to design an action policy that can approximate" that of an oracle, which has access to the reward model, the channel parameter, and the predictive distribution of the true context from the observed noisy context. In a Bayesian framework, we introduce a Thompson sampling algorithm for Gaussian bandits with Gaussian context noise. Adopting an information-theoretic analysis, we demonstrate the Bayesian regret of our algorithm concerning the oracle's action policy. We also extend this problem to a scenario where the agent observes the true context with some delay after receiving the reward and show that delayed true contexts lead to lower Bayesian regret. Finally, we empirically demonstrate the performance of the proposed algorithms against baselines.

Federated Stochastic Bandit Learning with Unobserved Context

We study the problem of federated stochastic multi-arm contextual bandits with unknown contexts, in which M agents are faced with different bandits and collaborate to learn. The communication model consists of a central server and the agents share their estimates with the central server periodically to learn to choose optimal actions in order to minimize the total regret. We assume that the exact contexts are not observable and the agents observe only a distribution of the contexts. Such a situation arises, for instance, when the context itself is a noisy measurement or based on a prediction mechanism. Our goal is to develop a distributed and federated algorithm that facilitates collaborative learning among the agents to select a sequence of optimal actions so as to maximize the cumulative reward. By performing a feature vector transformation, we propose an elimination-based algorithm and prove the regret bound for linearly parametrized reward functions. Finally, we validated the performance of our algorithm and compared it with another baseline approach using numerical simulations on synthetic data and on the real-world movielens dataset.

Distributed Stochastic Bandit Learning with Context Distributions

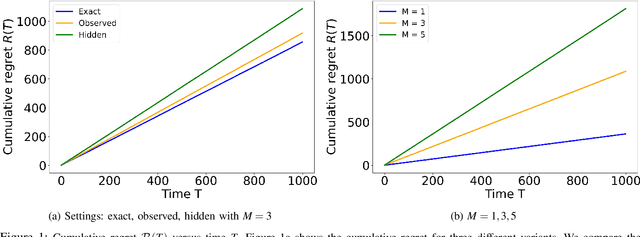
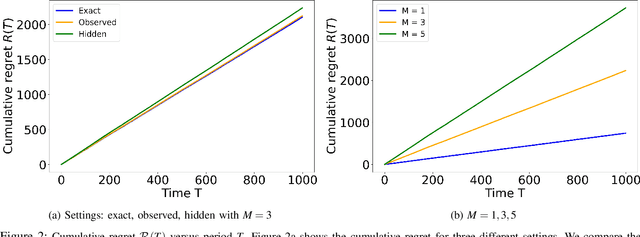
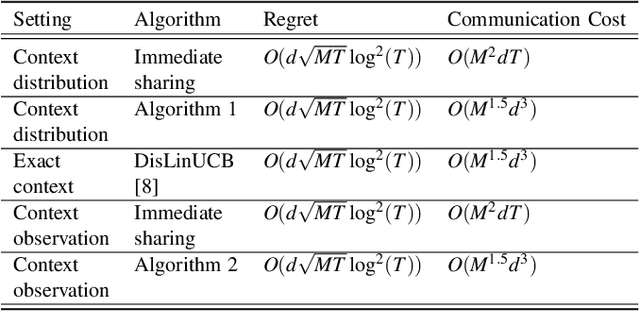
We study the problem of distributed stochastic multi-arm contextual bandit with unknown contexts, in which M agents work collaboratively to choose optimal actions under the coordination of a central server in order to minimize the total regret. In our model, an adversary chooses a distribution on the set of possible contexts and the agents observe only the context distribution and the exact context is unknown to the agents. Such a situation arises, for instance, when the context itself is a noisy measurement or based on a prediction mechanism as in weather forecasting or stock market prediction. Our goal is to develop a distributed algorithm that selects a sequence of optimal actions to maximize the cumulative reward. By performing a feature vector transformation and by leveraging the UCB algorithm, we propose a UCB algorithm for stochastic bandits with context distribution and prove that our algorithm achieves a regret and communications bounds of $O(d\sqrt{MT}log^2T)$ and $O(M^{1.5}d^3)$, respectively, for linearly parametrized reward functions. We also consider a case where the agents observe the actual context after choosing the action. For this setting we presented a modified algorithm that utilizes the additional information to achieve a tighter regret bound. Finally, we validated the performance of our algorithms and compared it with other baseline approaches using extensive simulations on synthetic data and on the real world movielens dataset.