AltGDmin: Alternating GD and Minimization for Partly-Decoupled (Federated) Optimization

This article describes a novel optimization solution framework, called alternating gradient descent (GD) and minimization (AltGDmin), that is useful for many problems for which alternating minimization (AltMin) is a popular solution. AltMin is a special case of the block coordinate descent algorithm that is useful for problems in which minimization w.r.t one subset of variables keeping the other fixed is closed form or otherwise reliably solved. Denote the two blocks/subsets of the optimization variables Z by Za, Zb, i.e., Z = {Za, Zb}. AltGDmin is often a faster solution than AltMin for any problem for which (i) the minimization over one set of variables, Zb, is much quicker than that over the other set, Za; and (ii) the cost function is differentiable w.r.t. Za. Often, the reason for one minimization to be quicker is that the problem is ``decoupled" for Zb and each of the decoupled problems is quick to solve. This decoupling is also what makes AltGDmin communication-efficient for federated settings. Important examples where this assumption holds include (a) low rank column-wise compressive sensing (LRCS), low rank matrix completion (LRMC), (b) their outlier-corrupted extensions such as robust PCA, robust LRCS and robust LRMC; (c) phase retrieval and its sparse and low-rank model based extensions; (d) tensor extensions of many of these problems such as tensor LRCS and tensor completion; and (e) many partly discrete problems where GD does not apply -- such as clustering, unlabeled sensing, and mixed linear regression. LRCS finds important applications in multi-task representation learning and few shot learning, federated sketching, and accelerated dynamic MRI. LRMC and robust PCA find important applications in recommender systems, computer vision and video analytics.

Few Shot Alternating GD and Minimization for Generalizable Real-Time MRI

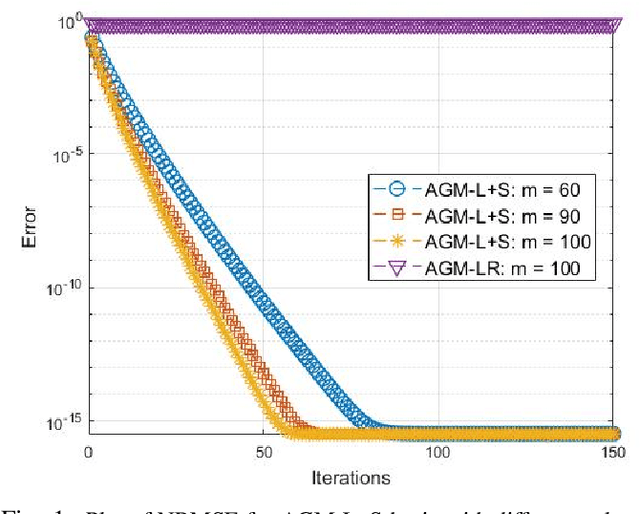
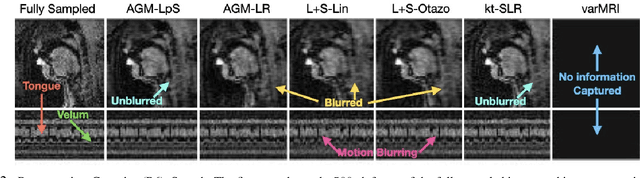
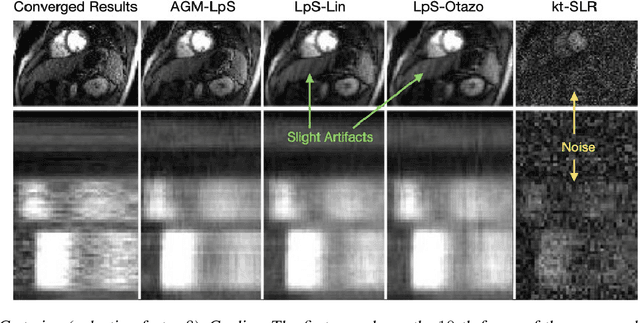
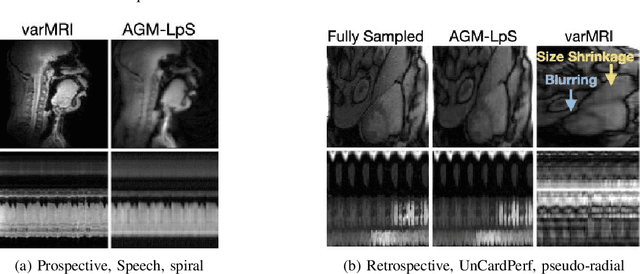
This work introduces a novel near real-time (real-time after an initial short delay) MRI solution that handles motion well and is generalizable. Here, real-time means the algorithm works well on a highly accelerated scan, is zero-latency (reconstructs a new frame as soon as MRI data for it arrives), and is fast enough, i.e., the time taken to process a frame is comparable to the scan time per frame or lesser. We demonstrate its generalizability through experiments on 6 prospective datasets and 17 retrospective datasets that span multiple different applications -- speech larynx imaging, brain, ungated cardiac perfusion, cardiac cine, cardiac OCMR, abdomen; sampling schemes -- Cartesian, pseudo-radial, radial, spiral; and sampling rates -- ranging from 6x to 4 radial lines per frame. Comparisons with a large number of existing real-time and batch methods, including unsupervised and supervised deep learning methods, show the power and speed of our approach.

Fast and Sample Efficient Multi-Task Representation Learning in Stochastic Contextual Bandits

We study how representation learning can improve the learning efficiency of contextual bandit problems. We study the setting where we play T contextual linear bandits with dimension d simultaneously, and these T bandit tasks collectively share a common linear representation with a dimensionality of r much smaller than d. We present a new algorithm based on alternating projected gradient descent (GD) and minimization estimator to recover a low-rank feature matrix. Using the proposed estimator, we present a multi-task learning algorithm for linear contextual bandits and prove the regret bound of our algorithm. We presented experiments and compared the performance of our algorithm against benchmark algorithms.

Noisy Low Rank Column-wise Sensing

This letter studies the AltGDmin algorithm for solving the noisy low rank column-wise sensing (LRCS) problem. Our sample complexity guarantee improves upon the best existing one by a factor $\max(r, \log(1/\epsilon))/r$ where $r$ is the rank of the unknown matrix and $\epsilon$ is the final desired accuracy. A second contribution of this work is a detailed comparison of guarantees from all work that studies the exact same mathematical problem as LRCS, but refers to it by different names.

Efficient Federated Low Rank Matrix Completion

In this work, we develop and analyze a Gradient Descent (GD) based solution, called Alternating GD and Minimization (AltGDmin), for efficiently solving the low rank matrix completion (LRMC) in a federated setting. LRMC involves recovering an $n \times q$ rank-$r$ matrix $\Xstar$ from a subset of its entries when $r \ll \min(n,q)$. Our theoretical guarantees (iteration and sample complexity bounds) imply that AltGDmin is the most communication-efficient solution in a federated setting, is one of the fastest, and has the second best sample complexity among all iterative solutions to LRMC. In addition, we also prove two important corollaries. (a) We provide a guarantee for AltGDmin for solving the noisy LRMC problem. (b) We show how our lemmas can be used to provide an improved sample complexity guarantee for AltMin, which is the fastest centralized solution.

A Fast Algorithm for Low Rank + Sparse column-wise Compressive Sensing

This paper focuses studies the following low rank + sparse (LR+S) column-wise compressive sensing problem. We aim to recover an $n \times q$ matrix, $\X^* =[ \x_1^*, \x_2^*, \cdots , \x_q^*]$ from $m$ independent linear projections of each of its $q$ columns, given by $\y_k :=\A_k\x_k^*$, $k \in [q]$. Here, $\y_k$ is an $m$-length vector with $m < n$. We assume that the matrix $\X^*$ can be decomposed as $\X^*=\L^*+\S^*$, where $\L^*$ is a low rank matrix of rank $r << \min(n,q)$ and $\S^*$ is a sparse matrix. Each column of $\S$ contains $\rho$ non-zero entries. The matrices $\A_k$ are known and mutually independent for different $k$. To address this recovery problem, we propose a novel fast GD-based solution called AltGDmin-LR+S, which is memory and communication efficient. We numerically evaluate its performance by conducting a detailed simulation-based study.

Byzantine-Resilient Federated PCA and Low Rank Matrix Recovery

In this work we consider the problem of estimating the principal subspace (span of the top r singular vectors) of a symmetric matrix in a federated setting, when each node has access to estimates of this matrix. We study how to make this problem Byzantine resilient. We introduce a novel provably Byzantine-resilient, communication-efficient, and private algorithm, called Subspace-Median, to solve it. We also study the most natural solution for this problem, a geometric median based modification of the federated power method, and explain why it is not useful. We consider two special cases of the resilient subspace estimation meta-problem - federated principal components analysis (PCA) and the spectral initialization step of horizontally federated low rank column-wise sensing (LRCCS) in this work. For both these problems we show how Subspace Median provides a resilient solution that is also communication-efficient. Median of Means extensions are developed for both problems. Extensive simulation experiments are used to corroborate our theoretical guarantees. Our second contribution is a complete AltGDmin based algorithm for Byzantine-resilient horizontally federated LRCCS and guarantees for it. We do this by developing a geometric median of means estimator for aggregating the partial gradients computed at each node, and using Subspace Median for initialization.

Fast Low Rank column-wise Compressive Sensing for Accelerated Dynamic MRI

This work develops a novel set of algorithms, alternating Gradient Descent (GD) and minimization for MRI (altGDmin-MRI1 and altGDmin-MRI2), for accelerated dynamic MRI by assuming an approximate low-rank (LR) model on the matrix formed by the vectorized images of the sequence. The LR model itself is well-known in the MRI literature; our contribution is the novel GD-based algorithms which are much faster, memory efficient, and general compared with existing work; and careful use of a 3-level hierarchical LR model. By general, we mean that, with a single choice of parameters, our method provides accurate reconstructions for multiple accelerated dynamic MRI applications, multiple sampling rates and sampling schemes. We show that our methods outperform many of the popular existing approaches while also being faster than all of them, on average. This claim is based on comparisons on 8 different retrospectively under sampled multi-coil dynamic MRI applications, sampled using either 1D Cartesian or 2D pseudo radial under sampling, at multiple sampling rates. Evaluations on some prospectively under sampled datasets are also provided. Our second contribution is a mini-batch subspace tracking extension that can process new measurements and return reconstructions within a short delay after they arrive. The recovery algorithm itself is also faster than its batch counterpart.

Non-Convex Structured Phase Retrieval

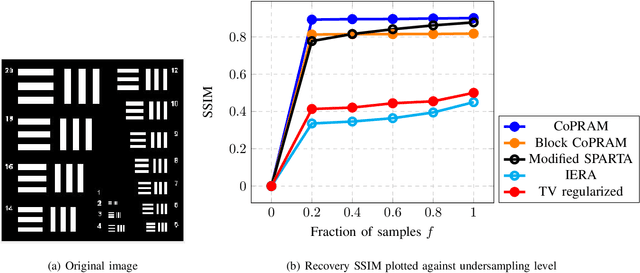
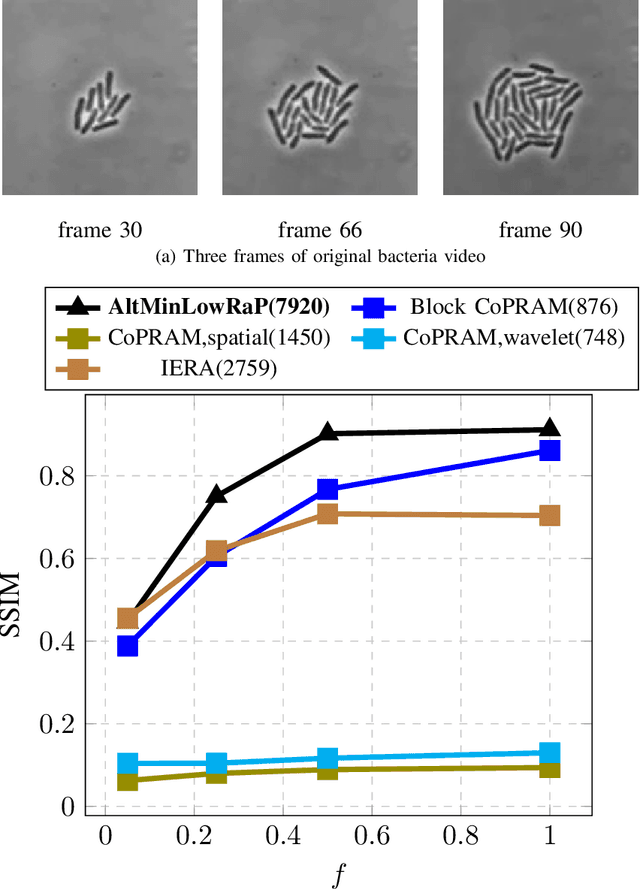
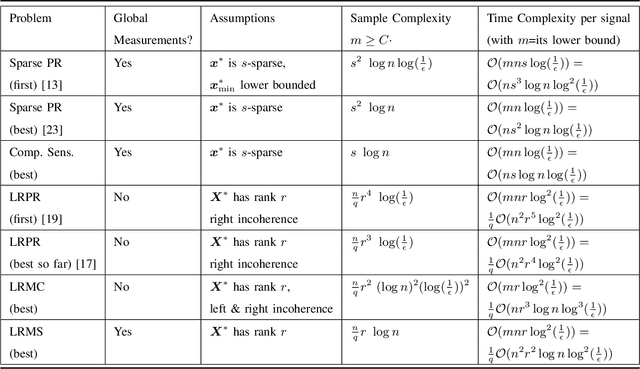
Phase retrieval (PR), also sometimes referred to as quadratic sensing, is a problem that occurs in numerous signal and image acquisition domains ranging from optics, X-ray crystallography, Fourier ptychography, sub-diffraction imaging, and astronomy. In each of these domains, the physics of the acquisition system dictates that only the magnitude (intensity) of certain linear projections of the signal or image can be measured. Without any assumptions on the unknown signal, accurate recovery necessarily requires an over-complete set of measurements. The only way to reduce the measurements/sample complexity is to place extra assumptions on the unknown signal/image. A simple and practically valid set of assumptions is obtained by exploiting the structure inherently present in many natural signals or sequences of signals. Two commonly used structural assumptions are (i) sparsity of a given signal/image or (ii) a low rank model on the matrix formed by a set, e.g., a time sequence, of signals/images. Both have been explored for solving the PR problem in a sample-efficient fashion. This article describes this work, with a focus on non-convex approaches that come with sample complexity guarantees under simple assumptions. We also briefly describe other different types of structural assumptions that have been used in recent literature.