Efficient Federated Low Rank Matrix Completion

In this work, we develop and analyze a Gradient Descent (GD) based solution, called Alternating GD and Minimization (AltGDmin), for efficiently solving the low rank matrix completion (LRMC) in a federated setting. LRMC involves recovering an $n \times q$ rank-$r$ matrix $\Xstar$ from a subset of its entries when $r \ll \min(n,q)$. Our theoretical guarantees (iteration and sample complexity bounds) imply that AltGDmin is the most communication-efficient solution in a federated setting, is one of the fastest, and has the second best sample complexity among all iterative solutions to LRMC. In addition, we also prove two important corollaries. (a) We provide a guarantee for AltGDmin for solving the noisy LRMC problem. (b) We show how our lemmas can be used to provide an improved sample complexity guarantee for AltMin, which is the fastest centralized solution.

r-local sensing: Improved algorithm and applications

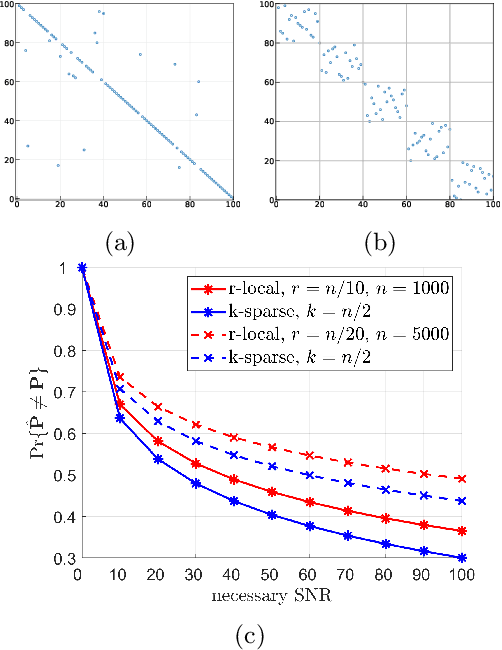
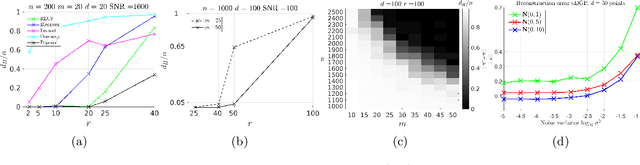
The unlabeled sensing problem is to solve a noisy linear system of equations under unknown permutation of the measurements. We study a particular case of the problem where the permutations are restricted to be r-local, i.e. the permutation matrix is block diagonal with r x r blocks. Assuming a Gaussian measurement matrix, we argue that the r-local permutation model is more challenging compared to a recent sparse permutation model. We propose a proximal alternating minimization algorithm for the general unlabeled sensing problem that provably converges to a first order stationary point. Applied to the r-local model, we show that the resulting algorithm is efficient. We validate the algorithm on synthetic and real datasets. We also formulate the 1-d unassigned distance geometry problem as an unlabeled sensing problem with a structured measurement matrix.