Distributed Stochastic Bandit Learning with Context Distributions

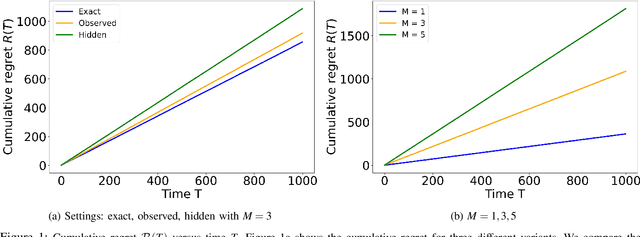
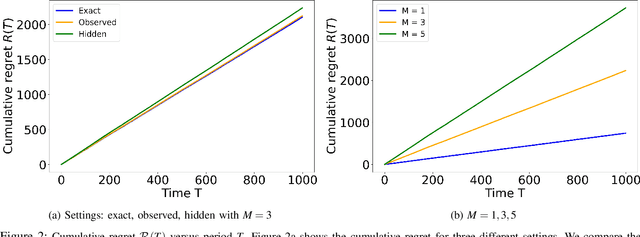
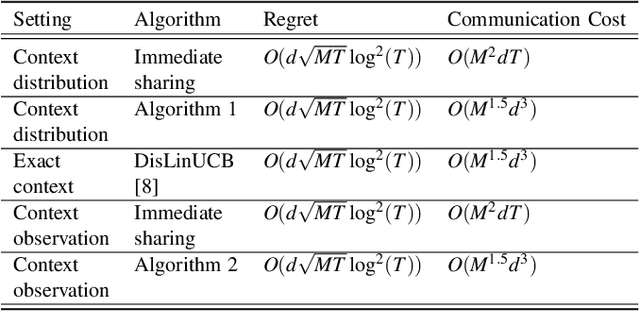
We study the problem of distributed stochastic multi-arm contextual bandit with unknown contexts, in which M agents work collaboratively to choose optimal actions under the coordination of a central server in order to minimize the total regret. In our model, an adversary chooses a distribution on the set of possible contexts and the agents observe only the context distribution and the exact context is unknown to the agents. Such a situation arises, for instance, when the context itself is a noisy measurement or based on a prediction mechanism as in weather forecasting or stock market prediction. Our goal is to develop a distributed algorithm that selects a sequence of optimal actions to maximize the cumulative reward. By performing a feature vector transformation and by leveraging the UCB algorithm, we propose a UCB algorithm for stochastic bandits with context distribution and prove that our algorithm achieves a regret and communications bounds of $O(d\sqrt{MT}log^2T)$ and $O(M^{1.5}d^3)$, respectively, for linearly parametrized reward functions. We also consider a case where the agents observe the actual context after choosing the action. For this setting we presented a modified algorithm that utilizes the additional information to achieve a tighter regret bound. Finally, we validated the performance of our algorithms and compared it with other baseline approaches using extensive simulations on synthetic data and on the real world movielens dataset.