An Optimal Energy Efficient Design of Artificial Noise for Preventing Power Leakage based Side-Channel Attacks

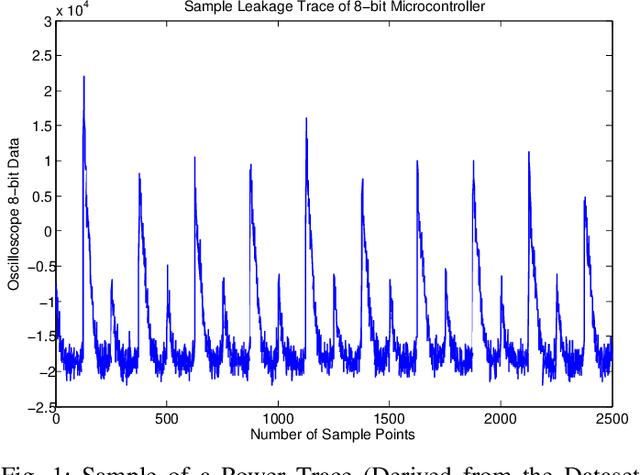
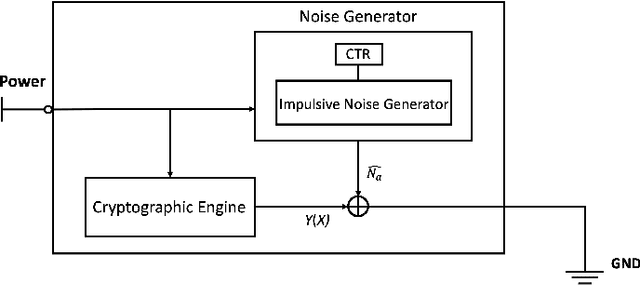
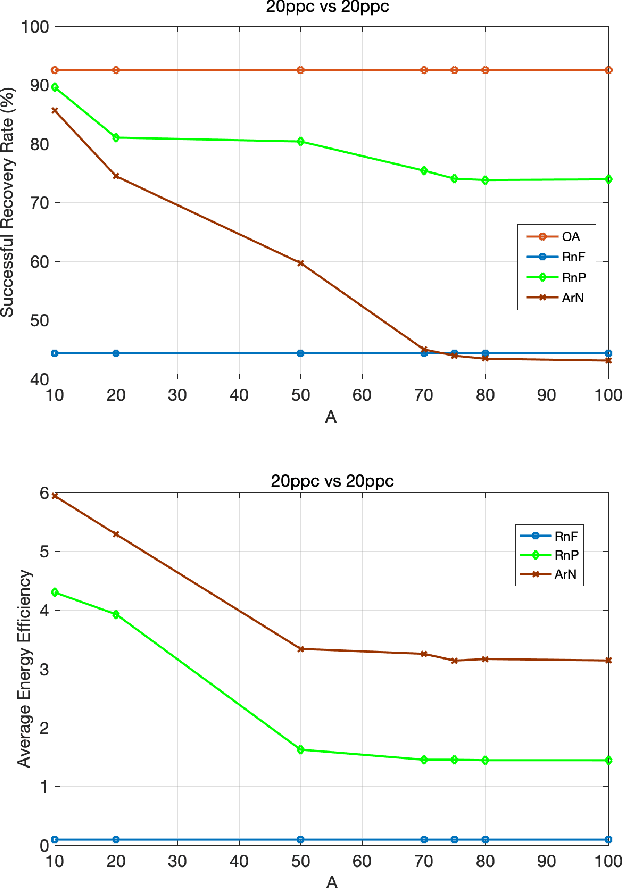
Side-channel attacks (SCAs), which infer secret information (for example secret keys) by exploiting information that leaks from the implementation (such as power consumption), have been shown to be a non-negligible threat to modern cryptographic implementations and devices in recent years. Hence, how to prevent side-channel attacks on cryptographic devices has become an important problem. One of the widely used countermeasures to against power SCAs is the injection of random noise sequences into the raw leakage traces. However, the indiscriminate injection of random noise can lead to significant increases in energy consumption in device, and ways must be found to reduce the amount of energy in noise generation while keeping the side-channel invisible. In this paper, we propose an optimal energy-efficient design for artificial noise generation to prevent side-channel attacks. This approach exploits the sparsity among the leakage traces. We model the side-channel as a communication channel, which allows us to use channel capacity to measure the mutual information between the secret and the leakage traces. For a given energy budget in the noise generation, we obtain the optimal design of the artificial noise injection by solving the side-channel's channel capacity minimization problem. The experimental results also validate the effectiveness of our proposed scheme.

Independent Reinforcement Learning for Weakly Cooperative Multiagent Traffic Control Problem

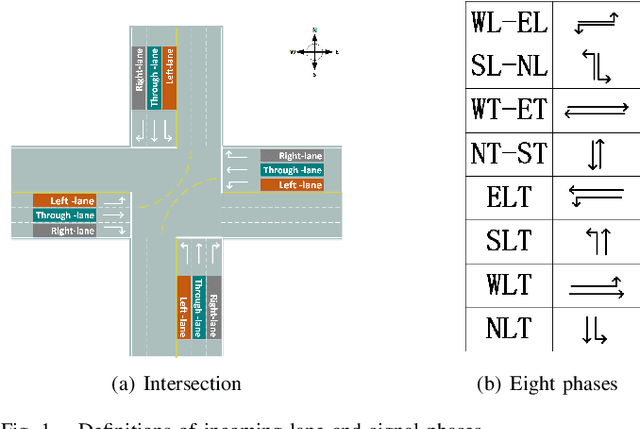
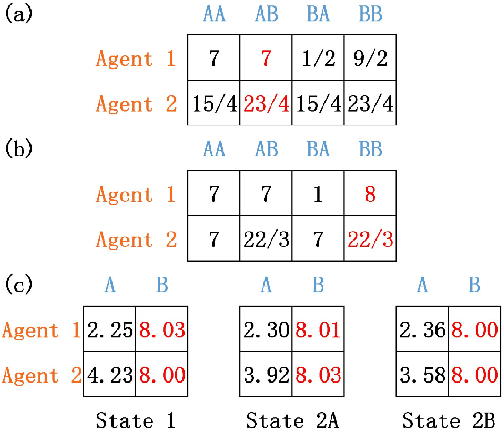
The adaptive traffic signal control (ATSC) problem can be modeled as a multiagent cooperative game among urban intersections, where intersections cooperate to optimize their common goal. Recently, reinforcement learning (RL) has achieved marked successes in managing sequential decision making problems, which motivates us to apply RL in the ASTC problem. Here we use independent reinforcement learning (IRL) to solve a complex traffic cooperative control problem in this study. One of the largest challenges of this problem is that the observation information of intersection is typically partially observable, which limits the learning performance of IRL algorithms. To this, we model the traffic control problem as a partially observable weak cooperative traffic model (PO-WCTM) to optimize the overall traffic situation of a group of intersections. Different from a traditional IRL task that averages the returns of all agents in fully cooperative games, the learning goal of each intersection in PO-WCTM is to reduce the cooperative difficulty of learning, which is also consistent with the traffic environment hypothesis. We also propose an IRL algorithm called Cooperative Important Lenient Double DQN (CIL-DDQN), which extends Double DQN (DDQN) algorithm using two mechanisms: the forgetful experience mechanism and the lenient weight training mechanism. The former mechanism decreases the importance of experiences stored in the experience reply buffer, which deals with the problem of experience failure caused by the strategy change of other agents. The latter mechanism increases the weight experiences with high estimation and `leniently' trains the DDQN neural network, which improves the probability of the selection of cooperative joint strategies. Experimental results show that CIL-DDQN outperforms other methods in almost all performance indicators of the traffic control problem.

Quantum reinforcement learning in continuous action space

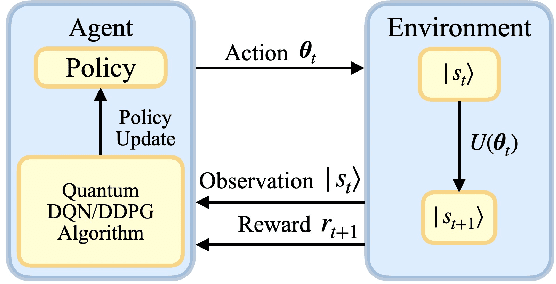
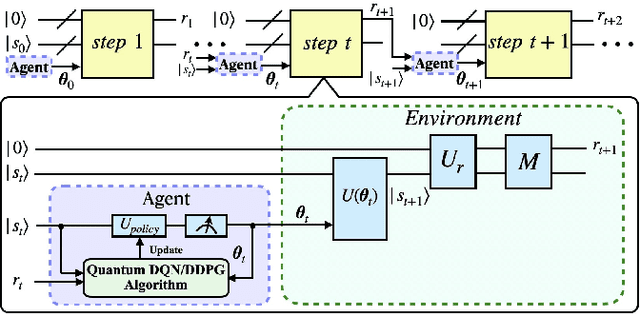
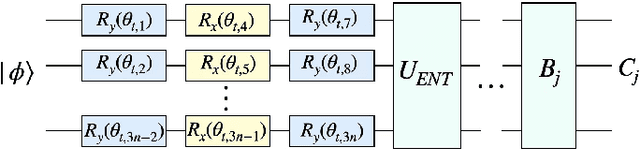
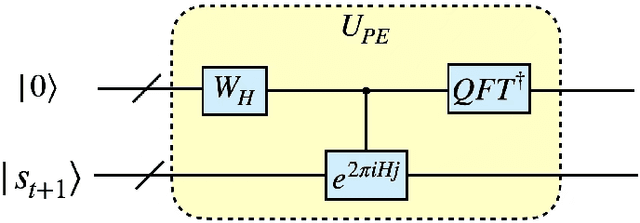
Quantum mechanics has the potential to speedup machine learning algorithms, including reinforcement learning(RL). Previous works have shown that quantum algorithms can efficiently solve RL problems in discrete action space, but could become intractable in continuous domain, suffering notably from the curse of dimensionality due to discretization. In this work, we propose an alternative quantum circuit design that can solve RL problems in continuous action space without the dimensionality problem. Specifically, we propose a quantum version of the Deep Deterministic Policy Gradient method constructed from quantum neural networks, with the potential advantage of obtaining an exponential speedup in gate complexity for each iteration. As applications, we demonstrate that quantum control tasks, including the eigenvalue problem and quantum state generation, can be formulated as sequential decision problems and solved by our method.