Dingding Wen
Quantum reinforcement learning in continuous action space
Jan 13, 2021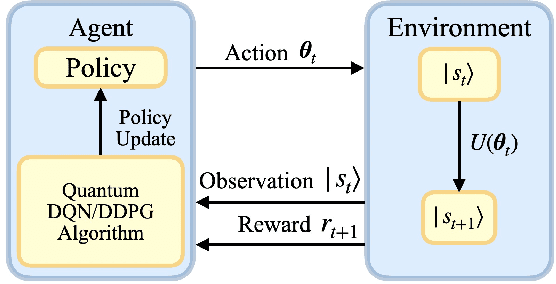
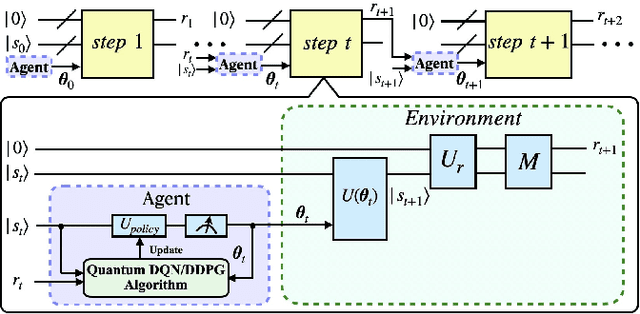
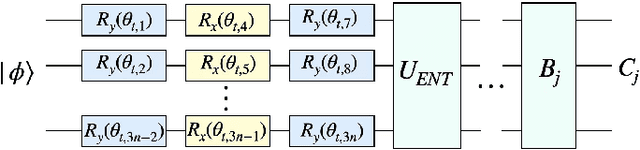
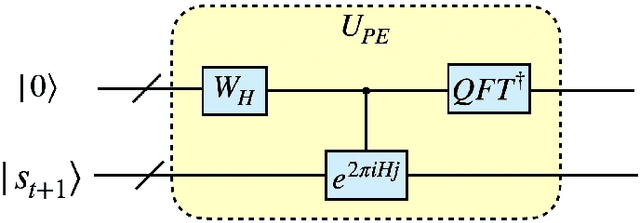
Abstract:Quantum mechanics has the potential to speedup machine learning algorithms, including reinforcement learning(RL). Previous works have shown that quantum algorithms can efficiently solve RL problems in discrete action space, but could become intractable in continuous domain, suffering notably from the curse of dimensionality due to discretization. In this work, we propose an alternative quantum circuit design that can solve RL problems in continuous action space without the dimensionality problem. Specifically, we propose a quantum version of the Deep Deterministic Policy Gradient method constructed from quantum neural networks, with the potential advantage of obtaining an exponential speedup in gate complexity for each iteration. As applications, we demonstrate that quantum control tasks, including the eigenvalue problem and quantum state generation, can be formulated as sequential decision problems and solved by our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge