Sample Efficient Learning of Body-Environment Interaction of an Under-Actuated System

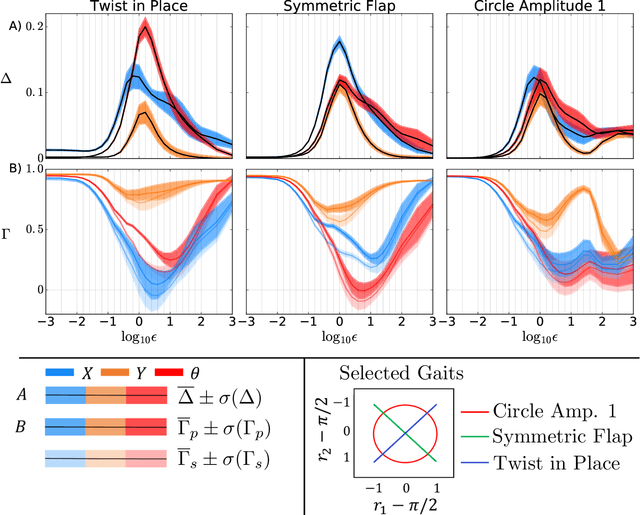
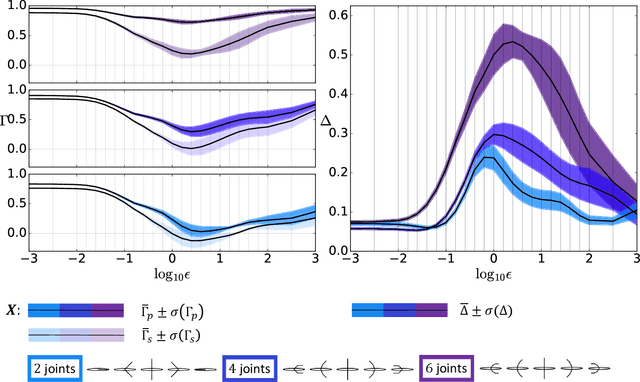
Geometric mechanics provides valuable insights into how biological and robotic systems use changes in shape to move by mechanically interacting with their environment. In high-friction environments it provides that the entire interaction is captured by the ``motility map''. Here we compare methods for learning the motility map from motion tracking data of a physical robot created specifically to test these methods by having under-actuated degrees of freedom and a hard to model interaction with its substrate. We compared four modeling approaches in terms of their ability to predict body velocity from shape change within the same gait, across gaits, and across speeds. Our results show a trade-off between simpler methods which are superior on small training datasets, and more sophisticated methods, which are superior when more training data is available.

Asymmetric Friction in Geometric Locomotion

Geometric mechanics models of locomotion have provided insight into how robots and animals use environmental interactions to convert internal shape changes into displacement through the world, encoding this relationship in a ``motility map''. A key class of such motility maps arises from (possibly anisotropic) linear drag acting on the system's individual body parts, formally described via Riemannian metrics on the motions of the system's individual body parts. The motility map can then be generated by invoking a sub-Riemannian constraint on the aggregate system motion under which the position velocity induced by a given shape velocity is that which minimizes the power dissipated via friction. The locomotion of such systems is ``geometric'' in the sense that the final position reached by the system depends only on the sequence of shapes that the system passes through, but not on the rate with which the shape changes are made. In this paper, we consider a far more general class of systems in which the drag may be not only anisotropic (with different coefficients for forward/backward and left/right motions), but also asymmetric (with different coefficients for forward and backward motions). Formally, including asymmetry in the friction replaces the Riemannian metrics on the body parts with Finsler metrics. We demonstrate that the sub-Riemannian approach to constructing the system motility map extends naturally to a sub-Finslerian approach and identify system properties analogous to the constraint curvature of sub-Riemannian systems that allow for the characterization of the system motion capabilities.

Learning the Geometric Mechanics of Robot Motion Using Gaussian Mixtures

Data-driven models of robot motion constructed using principles from Geometric Mechanics have been shown to produce useful predictions of robot motion for a variety of robots. For robots with a useful number of DoF, these geometric mechanics models can only be constructed in the neighborhood of a gait. Here we show how Gaussian Mixture Models (GMM) can be used as a form of manifold learning that learns the structure of the Geometric Mechanics "motility map" and demonstrate: [i] a sizable improvement in prediction quality when compared to the previously published methods; [ii] a method that can be applied to any motion dataset and not only periodic gait data; [iii] a way to pre-process the data-set to facilitate extrapolation in places where the motility map is known to be linear. Our results can be applied anywhere a data-driven geometric motion model might be useful.

Rapid Integrator for a Class of Multi-Contact Systems

Many problems in robotics involve creating or breaking multiple contacts nearly simultaneously or in an indeterminate order. We present a novel general purpose numerical integrator based on the theory of Event Selected Systems (ESS). Many multicontact models are ESS, which has recently been shown to imply that despite a discontinuous vector field, the flow of these systems is continuous, piecewise smooth, and has a well defined orbital derivative for all trajectories, which can be rapidly computed. We provide an elementary proof that our integrator is first-order accurate and verify numerically that it is in fact second-order accurate as its construction anticipated. We also compare our integrator, implemented in NumPy, to a MuJoCo simulation on models with 2 to 100 contacts, and confirm that the increase in simulation time per contact is nearly identical. The results suggest that this novel integrator can be invaluable for modelling and control in many robotics applications.

Modeling multi-legged robot locomotion with slipping and its experimental validation

Multi-legged robots with six or more legs are not in common use, despite designs with superior stability, maneuverability, and a low number of actuators being available for over 20 years. This may be in part due to the difficulty in modeling multi-legged motion with slipping and producing reliable predictions of body velocity. Here we present a detailed measurement of the foot contact forces in a hexapedal robot with multiple sliding contacts, and provide an algorithm for predicting these contact forces and the body velocity. The algorithm relies on the recently published observation that even while slipping, multi-legged robots are principally kinematic, and employ a friction law ansatz that allows us to compute the shape-change to body-velocity connection and the foot contact forces. This results in the ability to simulate motion plans for a large number of potentially slipping legs. In homogeneous environments, this can run in (parallel) logarithmic time of the planning horizon

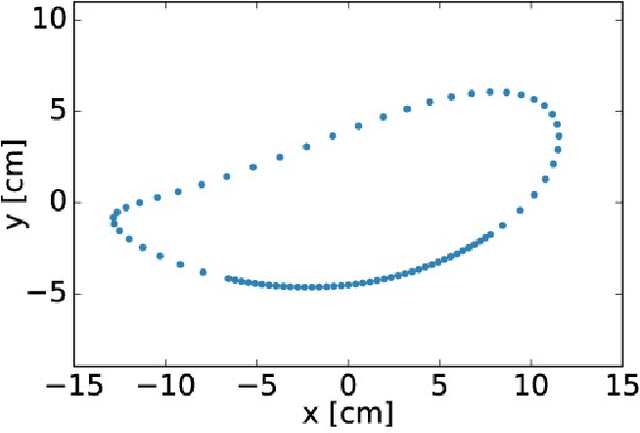
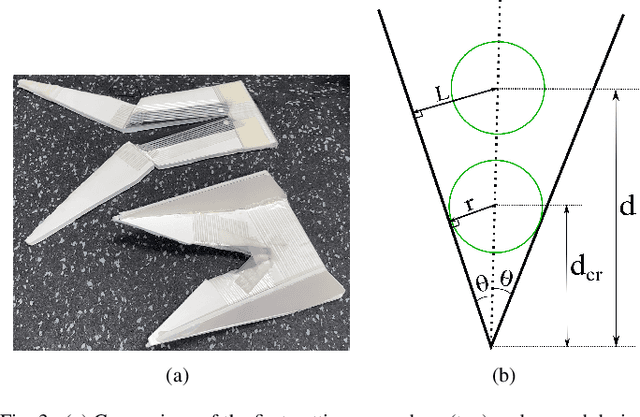
Dandelion-Picking Legged Robot

Agriculture is currently undergoing a robotics revolution, but robots using wheeled or treads suffer from known disadvantages: they are unable to move over rubble and steep or loose ground, and they trample continuous strips of land thereby reducing the viable crop area. Legged robots offer an alternative, but existing commercial legged robots are complex, expensive, and hard to maintain. We propose the use of multilegged robots using low-degree-of-freedom (low-DoF) legs and demonstrate our approach with a lawn pest control task: picking dandelions using our inexpensive and easy to fabricate BigANT robot. For this task we added an RGB-D camera to the robot. We also rigidly attached a flower picking appendage to the robot chassis. Thanks to the versatility of legs, the robot could be programmed to perform a ``swooping'' motion that allowed this 0-DoF appendage to pluck the flowers. Our results suggest that robots with six or more low-DoF legs may hit a sweet-spot for legged robots designed for agricultural applications by providing enough mobility, stability, and low complexity.

Optimizing Gait Libraries via a Coverage Metric

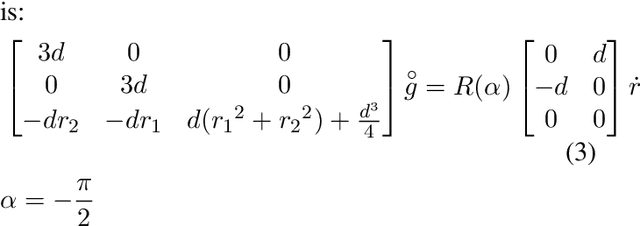
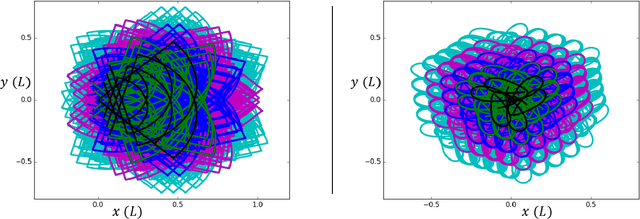
Many robots move through the world by composing locomotion primitives like steps and turns. To do so well, robots need not have primitives that make intuitive sense to humans. This becomes of paramount importance when robots are damaged and no longer move as designed. Here we propose a goal function we call "coverage", that represents the usefulness of a library of locomotion primitives in a manner agnostic to the particulars of the primitives themselves. We demonstrate the ability to optimize coverage on both simulated and physical robots, and show that coverage can be rapidly recovered after injury. This suggests that by optimizing for coverage, robots can sustain their ability to navigate through the world even in the face of significant mechanical failures. The benefits of this approach are enhanced by sample-efficient, data-driven approaches to system identification that can rapidly inform the optimization of primitives. We found that the number of degrees of freedom improved the rate of recovery of our simulated robots, a rare result in the fields of gait optimization and reinforcement learning. We showed that a robot with limbs made of tree branches (for which no CAD model or first principles model was available) is able to quickly find an effective high-coverage library of motion primitives. The optimized primitives are entirely non-obvious to a human observer, and thus are unlikely to be attainable through manual tuning.

Data-Driven Geometric System Identification for Shape-Underactuated Dissipative Systems

The study of systems whose movement is both geometric and dissipative offers an opportunity to quickly both identify models and optimize motion. Here, the geometry indicates reduction of the dynamics by environmental homogeneity while the dissipative nature minimizes the role of second order (inertial) features in the dynamics. In this work, we extend the tools of geometric system identification to "Shape-Underactuated Dissipative Systems (SUDS)" -- systems whose motions are kinematic, but whose actuation is restricted to a subset of the body shape coordinates. A large class of SUDS includes highly damped robots with series elastic actuators, and many soft robots. We validate the predictive quality of the models using simulations of a variety of viscous swimming systems. For a large class of SUDS, we show how the shape velocity actuation inputs can be directly converted into torque inputs suggesting that, e.g., systems with soft pneumatic actuators or dielectric elastomers, could be controlled in this way. Based on fundamental assumptions in the physics, we show how our model complexity scales linearly with the number of passive shape coordinates. This offers a large reduction on the number of trials needed to identify the system model from experimental data, and may reduce overfitting. The sample efficiency of our method suggests its use in modeling, control, and optimization in robotics, and as a tool for the study of organismal motion in friction dominated regimes.

Fast Recovery of Robot Behaviors

If robots are ever to achieve autonomous motion comparable to that exhibited by animals, they must acquire the ability to quickly recover motor behaviors when damage, malfunction, or environmental conditions compromise their ability to move effectively. We present an approach which allowed our robots and simulated robots to recover high-degree of freedom motor behaviors within a few dozen attempts. % Our approach employs a behavior specification expressing the desired behaviors in terms as rank ordered differential constraints. We show how factoring these constraints through an encoding templates produces a recipe for generalizing a previously optimized behavior to new circumstances in a form amenable to rapid learning. We further illustrate that adequate constraints are generically easy to determine in data-driven contexts. As illustration, we demonstrate our recovery approach on a physical 7 DOF hexapod robot, as well as a simulation of a 6 DOF 2D kinematic mechanism. In both cases we recovered a behavior functionally indistinguishable from the previously optimized motion.

Gait modeling and optimization for the perturbed Stokes regime

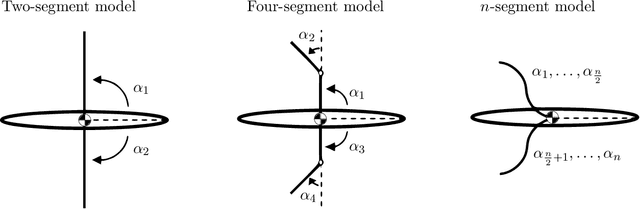
Many forms of locomotion, both natural and artificial, are dominated by viscous friction in the sense that without power expenditure they quickly come to a standstill. From geometric mechanics, it is known that for swimming at the "Stokesian" (viscous; zero Reynolds number) limit, the motion is governed by a reduced order "connection" model that describes how body shape change produces motion for the body frame with respect to the world. In the "perturbed Stokes regime" where inertial forces are still dominated by viscosity, but are not negligible (low Reynolds number), we show that motion is still governed by a functional relationship between shape velocity and body velocity, but this function is no longer linear in shape change rate. We derive this model using results from singular perturbation theory, and the theory of noncompact normally hyperbolic invariant manifolds (NHIMs). Using the theoretical properties of this reduced-order model, we develop an algorithm that estimates an approximation to the dynamics near a cyclic body shape change (a "gait") directly from observational data of shape and body motion. This extends our previous work which assumed kinematic "connection" models. To compare the old and new algorithms, we analyze simulated swimmers over a range of inertia to damping ratios. Our new class of models performs well on the Stokesian regime, and over several orders of magnitude outside it into the perturbed Stokes regime, where it gives significantly improved prediction accuracy compared to previous work. In addition to algorithmic improvements, we thereby present a new class of models that is of independent interest. Their application to data-driven modeling improves our ability to study the optimality of animal gaits, and our ability to use hardware-in-the-loop optimization to produce gaits for robots.