Hybrid Event Shaping to Stabilize Periodic Hybrid Orbits

Many controllers for legged robotic systems leverage open- or closed-loop control at discrete hybrid events to enhance stability. These controllers appear in several well studied phenomena such as the Raibert stepping controller, paddle juggling and swing leg retraction. This work introduces hybrid event shaping (HES): a generalized method for analyzing and producing stable hybrid event controllers. HES utilizes the saltation matrix, which gives a closed-form equation for the effect that hybrid events have on stability. We also introduce shape parameters, which are higher order terms that can be tuned completely independently from the system dynamics to promote stability. Optimization methods are used to produce values of these parameters that optimize a stability measure. Hybrid event shaping captures previously developed control methods while also producing new optimally stable trajectories without the need for continuous-domain feedback.

iLQR for Piecewise-Smooth Hybrid Dynamical Systems

Trajectory optimization is a popular strategy for planning trajectories for robotic systems. However, many robotic tasks require changing contact conditions, which is difficult due to the hybrid nature of the dynamics. The optimal sequence and timing of these modes are typically not known ahead of time. In this work, we extend the Iterative Linear Quadratic Regulator (iLQR) method to a class of piecewise smooth hybrid dynamical systems by allowing for changing hybrid modes in the forward pass, using the saltation matrix to update the gradient information in the backwards pass, and using a reference extension to account for mode mismatch. We demonstrate these changes on a variety of hybrid systems and compare the different strategies for computing the gradients.

Mapping Distributions through Hybrid Dynamical Systems and its Application to Kalman Filtering

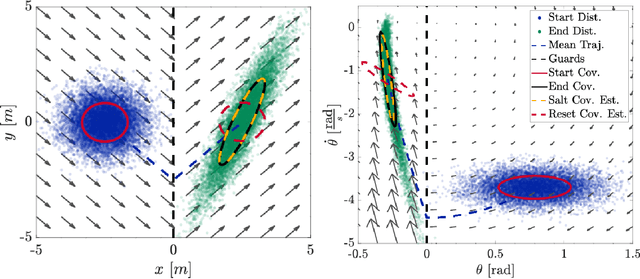
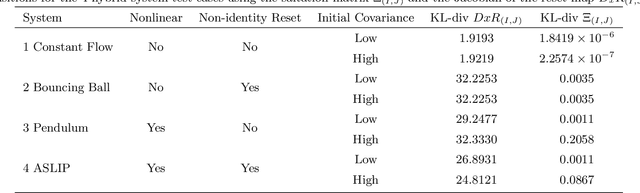
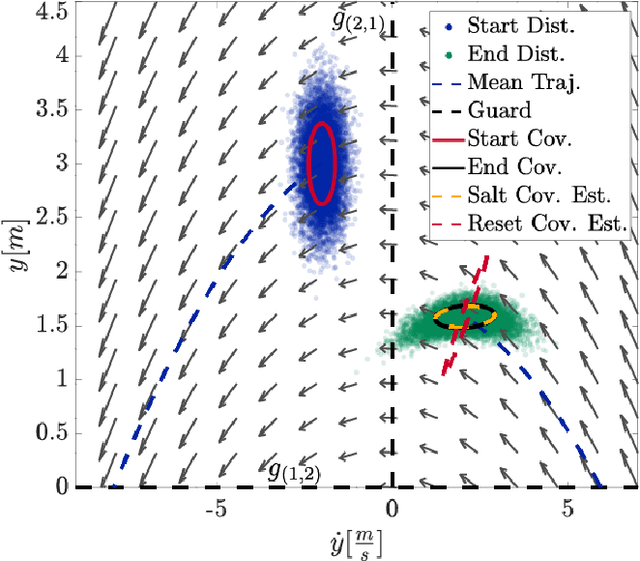
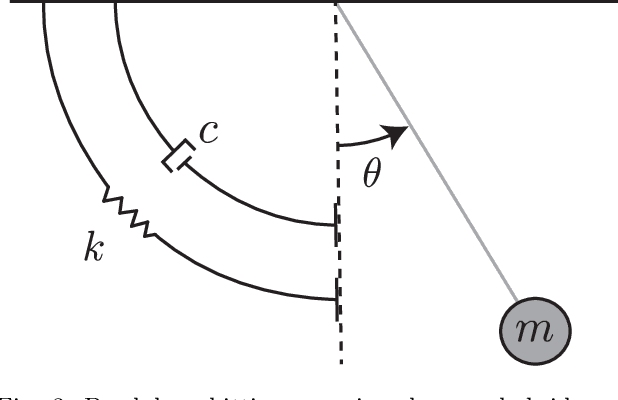
Many state estimation and control algorithms require knowledge of how probability distributions propagate through dynamical systems. However, despite hybrid dynamical systems becoming increasingly important in many fields, there has been little work on how to map probability distributions through hybrid transitions. Here, we derive a propagation law that employs the saltation matrix (a first-order update to the sensitivity equation) to formally compute how a distribution's second moment is mapped through an isolated transition in a hybrid dynamical system. This saltation matrix update for the second moment of a distribution is compared to both the true distribution and a naive method which utilizes the differential of the reset map. Using this covariance propagation law, we propose the Salted Kalman Filter (SKF), a natural extension of the Kalman Filter and Extended Kalman Filter to hybrid dynamical systems. Away from hybrid events, the SKF is a standard Kalman filter. When a hybrid event occurs, the saltation matrix plays an analogous role as that of the system dynamics, subsequently inducing a discrete modification to both the prediction and update steps. Simulation results from the SKF show a reduced mean squared error in state estimation compared to using the differential of the reset map, especially immediately after a hybrid transition event.

Fast Recovery of Robot Behaviors

If robots are ever to achieve autonomous motion comparable to that exhibited by animals, they must acquire the ability to quickly recover motor behaviors when damage, malfunction, or environmental conditions compromise their ability to move effectively. We present an approach which allowed our robots and simulated robots to recover high-degree of freedom motor behaviors within a few dozen attempts. % Our approach employs a behavior specification expressing the desired behaviors in terms as rank ordered differential constraints. We show how factoring these constraints through an encoding templates produces a recipe for generalizing a previously optimized behavior to new circumstances in a form amenable to rapid learning. We further illustrate that adequate constraints are generically easy to determine in data-driven contexts. As illustration, we demonstrate our recovery approach on a physical 7 DOF hexapod robot, as well as a simulation of a 6 DOF 2D kinematic mechanism. In both cases we recovered a behavior functionally indistinguishable from the previously optimized motion.