Hybrid Iterative Linear Quadratic Estimation: Optimal Estimation for Hybrid Systems

In this paper we present Hybrid iterative Linear Quadratic Estimation (HiLQE), an optimization based offline state estimation algorithm for hybrid dynamical systems. We utilize the saltation matrix, a first order approximation of the variational update through an event driven hybrid transition, to calculate gradient information through hybrid events in the backward pass of an iterative linear quadratic optimization over state estimates. This enables accurate computation of the value function approximation at each timestep. Additionally, the forward pass in the iterative algorithm is augmented with hybrid dynamics in the rollout. A reference extension method is used to account for varying impact times when comparing states for the feedback gain in noise calculation. The proposed method is demonstrated on an ASLIP hopper system with position measurements. In comparison to the Salted Kalman Filter (SKF), the algorithm presented here achieves a maximum of 63.55% reduction in estimation error magnitude over all state dimensions near impact events.

Saltation Matrices: The Essential Tool for Linearizing Hybrid Dynamical Systems

Hybrid dynamical systems, i.e. systems that have both continuous and discrete states, are ubiquitous in engineering, but are difficult to work with due to their discontinuous transitions. For example, a robot leg is able to exert very little control effort while it is in the air compared to when it is on the ground. When the leg hits the ground, the penetrating velocity instantaneously collapses to zero. These instantaneous changes in dynamics and discontinuities (or jumps) in state make standard smooth tools for planning, estimation, control, and learning difficult for hybrid systems. One of the key tools for accounting for these jumps is called the saltation matrix. The saltation matrix is the sensitivity update when a hybrid jump occurs and has been used in a variety of fields including robotics, power circuits, and computational neuroscience. This paper presents an intuitive derivation of the saltation matrix and discusses what it captures, where it has been used in the past, how it is used for linear and quadratic forms, how it is computed for rigid body systems with unilateral constraints, and some of the structural properties of the saltation matrix in these cases.

Hybrid iLQR Model Predictive Control for Contact Implicit Stabilization on Legged Robots

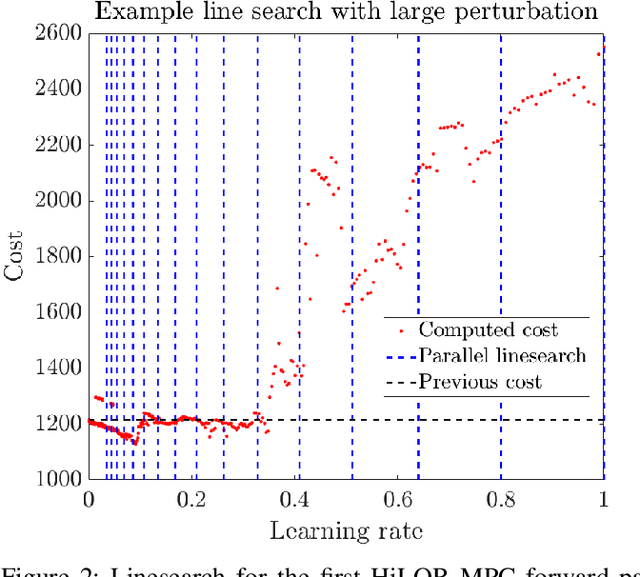
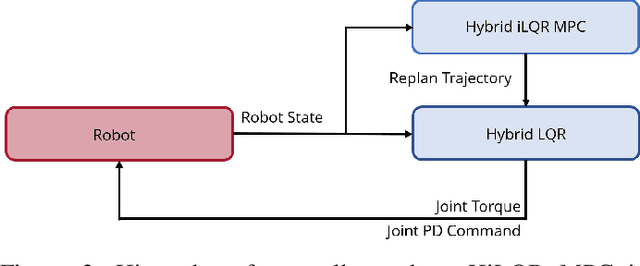
Model Predictive Control (MPC) is a popular strategy for controlling robots but is difficult for systems with contact due to the complex nature of hybrid dynamics. To implement MPC for systems with contact, dynamic models are often simplified or contact sequences fixed in time in order to plan trajectories efficiently. In this work, we extend Hybrid iterative Linear Quadratic Regulator to work in a MPC fashion (HiLQR MPC) by 1) modifying how the cost function is computed when contact modes do not align, 2) utilizing parallelizations when simulating rigid body dynamics, and 3) using efficient analytical derivative computations of the rigid body dynamics. The result is a system that can modify the contact sequence of the reference behavior and plan whole body motions cohesively -- which is crucial when dealing with large perturbations. HiLQR MPC is tested on two systems: first, the hybrid cost modification is validated on a simple actuated bouncing ball hybrid system. Then HiLQR MPC is compared against methods that utilize centroidal dynamic assumptions on a quadruped robot (Unitree A1). HiLQR MPC outperforms the centroidal methods in both simulation and hardware tests.

The Uncertainty Aware Salted Kalman Filter: State Estimation for Hybrid Systems with Uncertain Guards

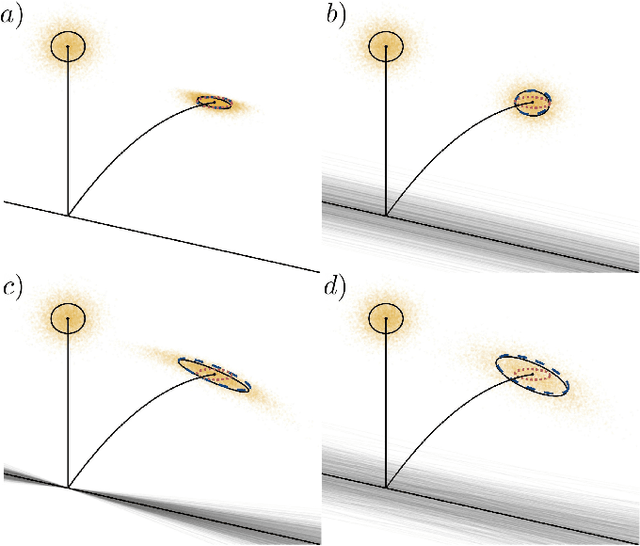
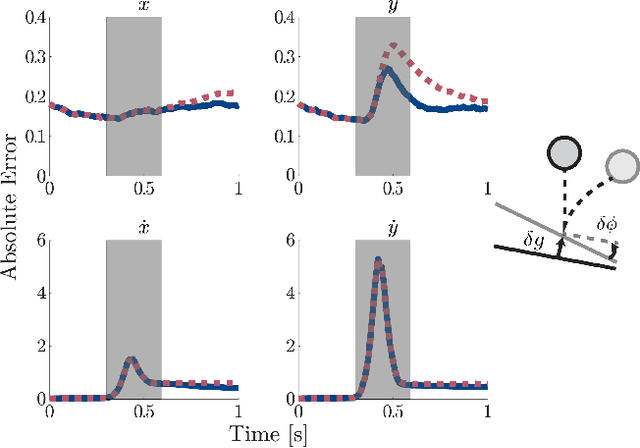
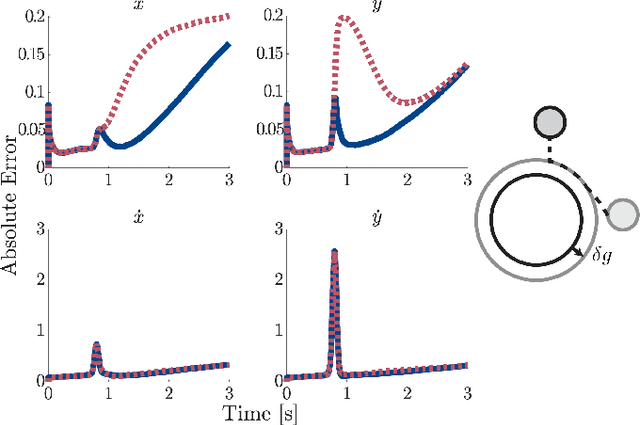
In this paper we present a method for updating robotic state belief through contact with uncertain surfaces and apply this update to a Kalman filter for more accurate state estimation. Examining how guard surface uncertainty affects the time spent in each mode, we derive a guard saltation matrix - which maps perturbations prior to hybrid events to perturbations after - accounting for additional variation in the resulting state. Additionally, we propose the use of parameterized reset functions - capturing how unknown parameters change how states are mapped from one mode to the next - the Jacobian of which accounts for the additional uncertainty in the resulting state. The accuracy of these mappings is shown by simulating sampled distributions through uncertain transition events and comparing the resulting covariances. Finally, we integrate these additional terms into the "uncertainty aware Salted Kalman Filter", uaSKF, and show a peak reduction in average estimation error by 24-60% on a variety of test conditions and systems.

Hybrid Event Shaping to Stabilize Periodic Hybrid Orbits

Many controllers for legged robotic systems leverage open- or closed-loop control at discrete hybrid events to enhance stability. These controllers appear in several well studied phenomena such as the Raibert stepping controller, paddle juggling and swing leg retraction. This work introduces hybrid event shaping (HES): a generalized method for analyzing and producing stable hybrid event controllers. HES utilizes the saltation matrix, which gives a closed-form equation for the effect that hybrid events have on stability. We also introduce shape parameters, which are higher order terms that can be tuned completely independently from the system dynamics to promote stability. Optimization methods are used to produce values of these parameters that optimize a stability measure. Hybrid event shaping captures previously developed control methods while also producing new optimally stable trajectories without the need for continuous-domain feedback.

iLQR for Piecewise-Smooth Hybrid Dynamical Systems

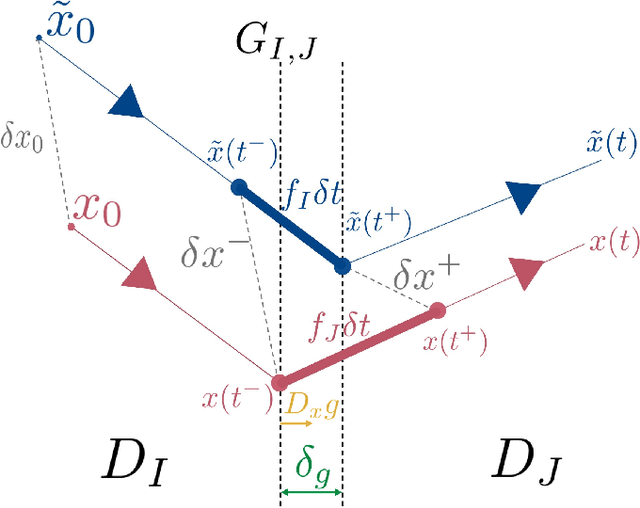
Trajectory optimization is a popular strategy for planning trajectories for robotic systems. However, many robotic tasks require changing contact conditions, which is difficult due to the hybrid nature of the dynamics. The optimal sequence and timing of these modes are typically not known ahead of time. In this work, we extend the Iterative Linear Quadratic Regulator (iLQR) method to a class of piecewise smooth hybrid dynamical systems by allowing for changing hybrid modes in the forward pass, using the saltation matrix to update the gradient information in the backwards pass, and using a reference extension to account for mode mismatch. We demonstrate these changes on a variety of hybrid systems and compare the different strategies for computing the gradients.

Mapping Distributions through Hybrid Dynamical Systems and its Application to Kalman Filtering

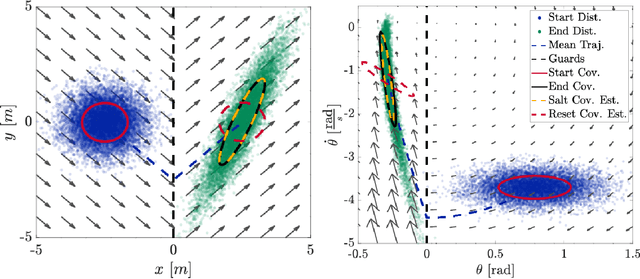
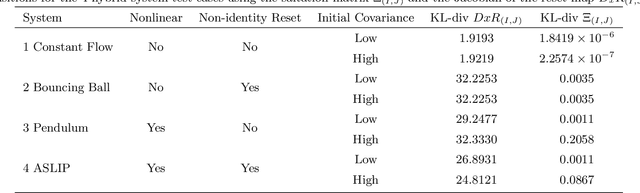
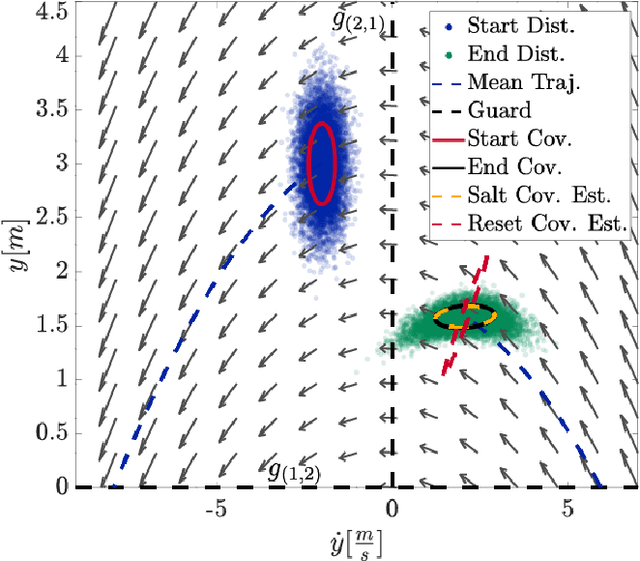
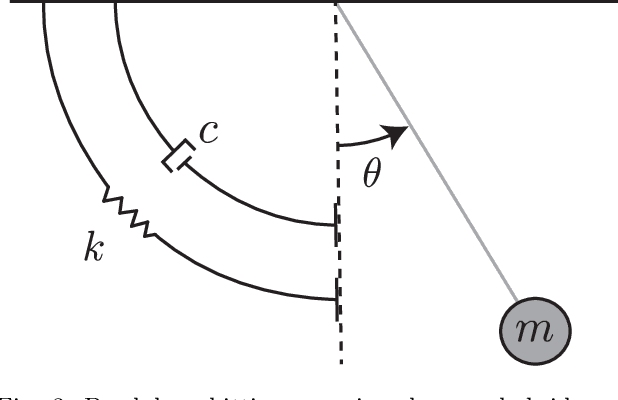
Many state estimation and control algorithms require knowledge of how probability distributions propagate through dynamical systems. However, despite hybrid dynamical systems becoming increasingly important in many fields, there has been little work on how to map probability distributions through hybrid transitions. Here, we derive a propagation law that employs the saltation matrix (a first-order update to the sensitivity equation) to formally compute how a distribution's second moment is mapped through an isolated transition in a hybrid dynamical system. This saltation matrix update for the second moment of a distribution is compared to both the true distribution and a naive method which utilizes the differential of the reset map. Using this covariance propagation law, we propose the Salted Kalman Filter (SKF), a natural extension of the Kalman Filter and Extended Kalman Filter to hybrid dynamical systems. Away from hybrid events, the SKF is a standard Kalman filter. When a hybrid event occurs, the saltation matrix plays an analogous role as that of the system dynamics, subsequently inducing a discrete modification to both the prediction and update steps. Simulation results from the SKF show a reduced mean squared error in state estimation compared to using the differential of the reset map, especially immediately after a hybrid transition event.