Multi-Momentum Observer Contact Estimation for Bipedal Robots

As bipedal robots become more and more popular in commercial and industrial settings, the ability to control them with a high degree of reliability is critical. To that end, this paper considers how to accurately estimate which feet are currently in contact with the ground so as to avoid improper control actions that could jeopardize the stability of the robot. Additionally, modern algorithms for estimating the position and orientation of a robot's base frame rely heavily on such contact mode estimates. Dedicated contact sensors on the feet can be used to estimate this contact mode, but these sensors are prone to noise, time delays, damage/yielding from repeated impacts with the ground, and are not available on every robot. To overcome these limitations, we propose a momentum observer based method for contact mode estimation that does not rely on such contact sensors. Often, momentum observers assume that the robot's base frame can be treated as an inertial frame. However, since many humanoids' legs represent a significant portion of the overall mass, the proposed method instead utilizes multiple simultaneous dynamic models. Each of these models assumes a different contact condition. A given contact assumption is then used to constrain the full dynamics in order to avoid assuming that either the body is an inertial frame or that a fully accurate estimate of body velocity is known. The (dis)agreement between each model's estimates and measurements is used to determine which contact mode is most likely using a Markov-style fusion method. The proposed method produces contact detection accuracy of up to 98.44% with a low noise simulation and 77.12% when utilizing data collect on the Sarcos Guardian XO robot (a hybrid humanoid/exoskeleton).

Hybrid Iterative Linear Quadratic Estimation: Optimal Estimation for Hybrid Systems

In this paper we present Hybrid iterative Linear Quadratic Estimation (HiLQE), an optimization based offline state estimation algorithm for hybrid dynamical systems. We utilize the saltation matrix, a first order approximation of the variational update through an event driven hybrid transition, to calculate gradient information through hybrid events in the backward pass of an iterative linear quadratic optimization over state estimates. This enables accurate computation of the value function approximation at each timestep. Additionally, the forward pass in the iterative algorithm is augmented with hybrid dynamics in the rollout. A reference extension method is used to account for varying impact times when comparing states for the feedback gain in noise calculation. The proposed method is demonstrated on an ASLIP hopper system with position measurements. In comparison to the Salted Kalman Filter (SKF), the algorithm presented here achieves a maximum of 63.55% reduction in estimation error magnitude over all state dimensions near impact events.

Double-Anonymous Review for Robotics

Prior research has investigated the benefits and costs of double-anonymous review (DAR, also known as double-blind review) in comparison to single-anonymous review (SAR) and open review (OR). Several review papers have attempted to compile experimental results in peer review research both broadly and in engineering and computer science. This document summarizes prior research in peer review that may inform decisions about the format of peer review in the field of robotics and makes some recommendations for potential next steps for robotics publication.

Saltation Matrices: The Essential Tool for Linearizing Hybrid Dynamical Systems

Hybrid dynamical systems, i.e. systems that have both continuous and discrete states, are ubiquitous in engineering, but are difficult to work with due to their discontinuous transitions. For example, a robot leg is able to exert very little control effort while it is in the air compared to when it is on the ground. When the leg hits the ground, the penetrating velocity instantaneously collapses to zero. These instantaneous changes in dynamics and discontinuities (or jumps) in state make standard smooth tools for planning, estimation, control, and learning difficult for hybrid systems. One of the key tools for accounting for these jumps is called the saltation matrix. The saltation matrix is the sensitivity update when a hybrid jump occurs and has been used in a variety of fields including robotics, power circuits, and computational neuroscience. This paper presents an intuitive derivation of the saltation matrix and discusses what it captures, where it has been used in the past, how it is used for linear and quadratic forms, how it is computed for rigid body systems with unilateral constraints, and some of the structural properties of the saltation matrix in these cases.

Convergent iLQR for Safe Trajectory Planning and Control of Legged Robots

In order to perform highly dynamic and agile maneuvers, legged robots typically spend time in underactuated domains (e.g. with feet off the ground) where the system has limited command of its acceleration and a constrained amount of time before transitioning to a new domain (e.g. foot touchdown). Meanwhile, these transitions can have instantaneous, unbounded effects on perturbations. These properties make it difficult for local feedback controllers to effectively recover from disturbances as the system evolves through underactuated domains and hybrid impact events. To address this, we utilize the fundamental solution matrix that characterizes the evolution of perturbations through a hybrid trajectory and its 2-norm, which represents the worst-case growth of perturbations. In this paper, the worst-case perturbation analysis is used to explicitly reason about the tracking performance of a hybrid trajectory and is incorporated in an iLQR framework to optimize a trajectory while taking into account the closed-loop convergence of the trajectory under an LQR tracking controller. The generated convergent trajectories are able to recover more effectively from perturbations, are more robust to large disturbances, and use less feedback control effort than trajectories generated with traditional optimization methods.

The Uncertainty Aware Salted Kalman Filter: State Estimation for Hybrid Systems with Uncertain Guards

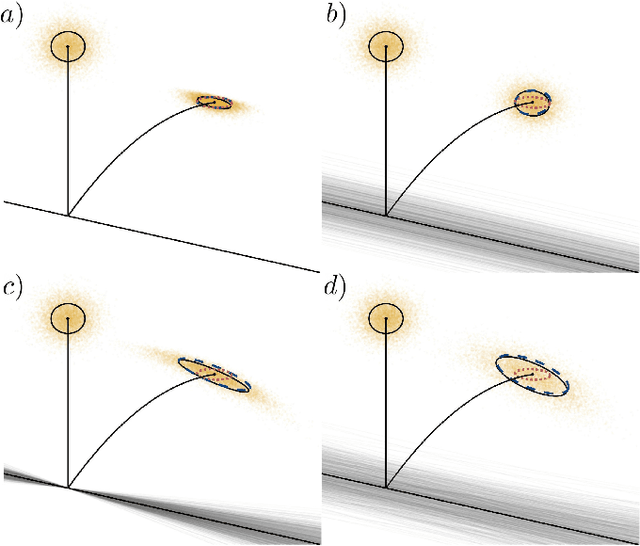
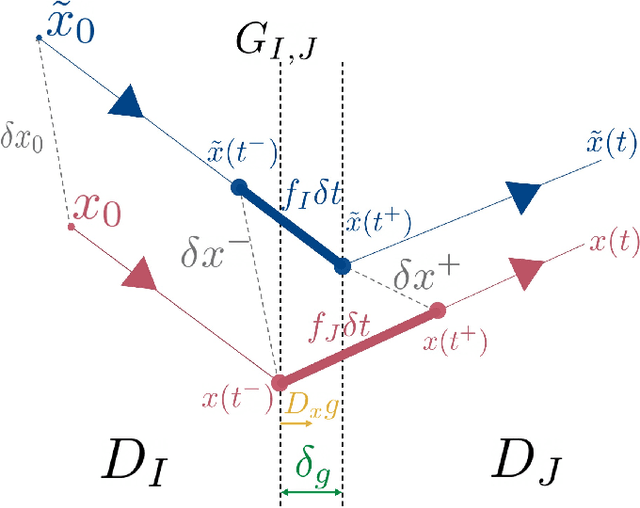
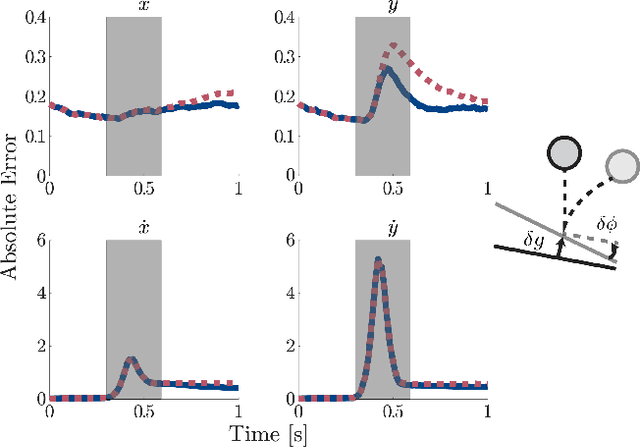
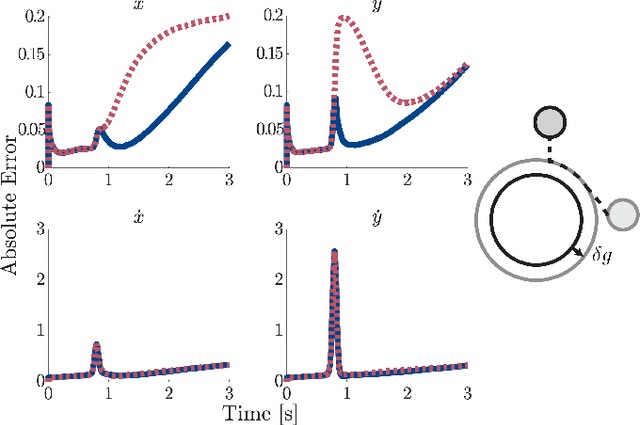
In this paper we present a method for updating robotic state belief through contact with uncertain surfaces and apply this update to a Kalman filter for more accurate state estimation. Examining how guard surface uncertainty affects the time spent in each mode, we derive a guard saltation matrix - which maps perturbations prior to hybrid events to perturbations after - accounting for additional variation in the resulting state. Additionally, we propose the use of parameterized reset functions - capturing how unknown parameters change how states are mapped from one mode to the next - the Jacobian of which accounts for the additional uncertainty in the resulting state. The accuracy of these mappings is shown by simulating sampled distributions through uncertain transition events and comparing the resulting covariances. Finally, we integrate these additional terms into the "uncertainty aware Salted Kalman Filter", uaSKF, and show a peak reduction in average estimation error by 24-60% on a variety of test conditions and systems.

Mapping Distributions through Hybrid Dynamical Systems and its Application to Kalman Filtering

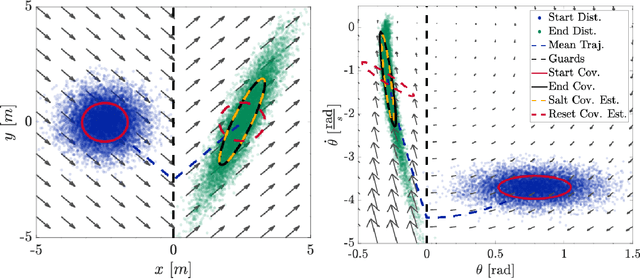
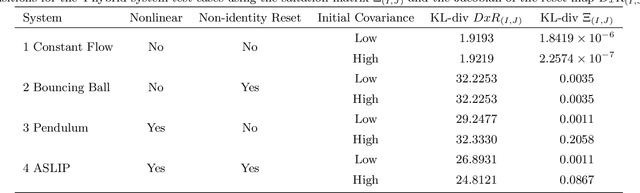
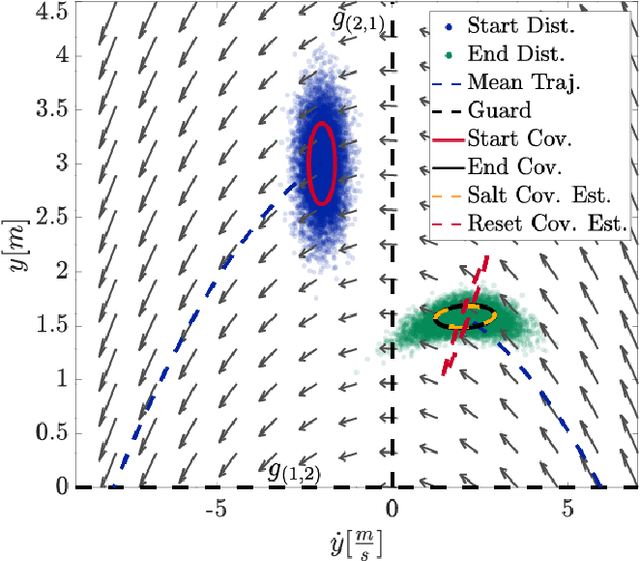
Many state estimation and control algorithms require knowledge of how probability distributions propagate through dynamical systems. However, despite hybrid dynamical systems becoming increasingly important in many fields, there has been little work on how to map probability distributions through hybrid transitions. Here, we derive a propagation law that employs the saltation matrix (a first-order update to the sensitivity equation) to formally compute how a distribution's second moment is mapped through an isolated transition in a hybrid dynamical system. This saltation matrix update for the second moment of a distribution is compared to both the true distribution and a naive method which utilizes the differential of the reset map. Using this covariance propagation law, we propose the Salted Kalman Filter (SKF), a natural extension of the Kalman Filter and Extended Kalman Filter to hybrid dynamical systems. Away from hybrid events, the SKF is a standard Kalman filter. When a hybrid event occurs, the saltation matrix plays an analogous role as that of the system dynamics, subsequently inducing a discrete modification to both the prediction and update steps. Simulation results from the SKF show a reduced mean squared error in state estimation compared to using the differential of the reset map, especially immediately after a hybrid transition event.