Mapping Distributions through Hybrid Dynamical Systems and its Application to Kalman Filtering

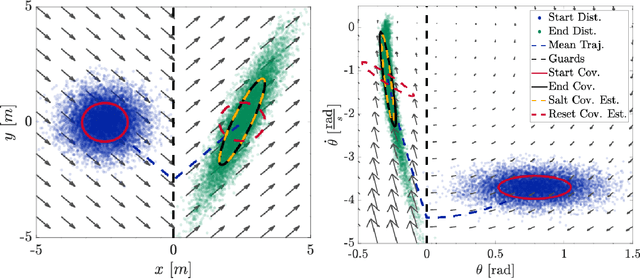
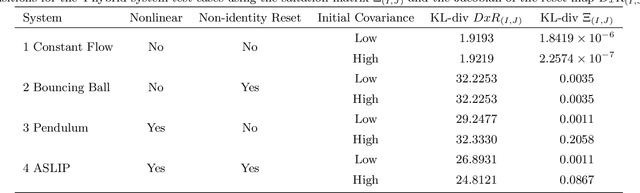
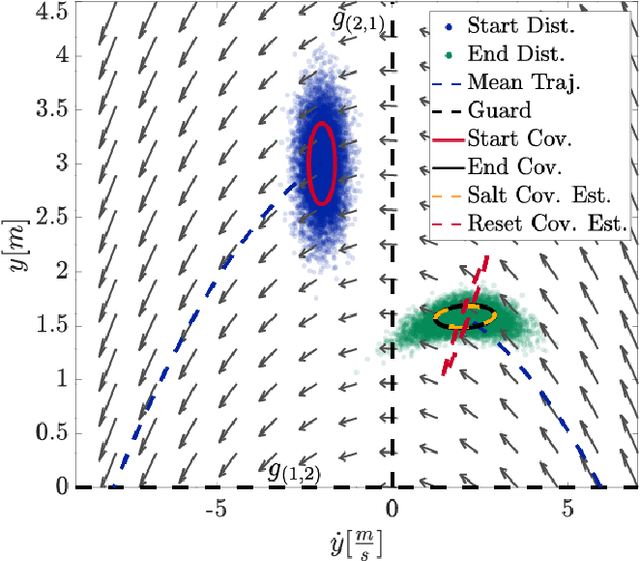
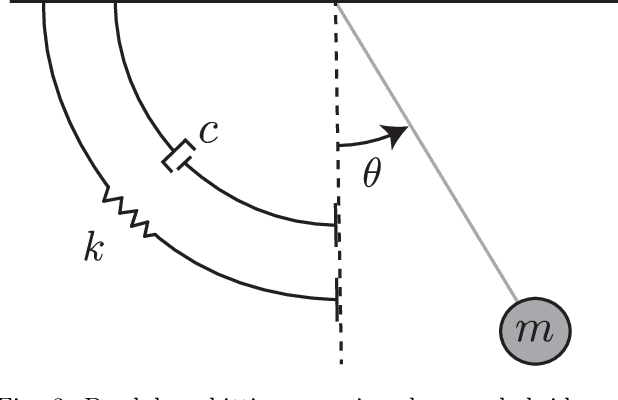
Many state estimation and control algorithms require knowledge of how probability distributions propagate through dynamical systems. However, despite hybrid dynamical systems becoming increasingly important in many fields, there has been little work on how to map probability distributions through hybrid transitions. Here, we derive a propagation law that employs the saltation matrix (a first-order update to the sensitivity equation) to formally compute how a distribution's second moment is mapped through an isolated transition in a hybrid dynamical system. This saltation matrix update for the second moment of a distribution is compared to both the true distribution and a naive method which utilizes the differential of the reset map. Using this covariance propagation law, we propose the Salted Kalman Filter (SKF), a natural extension of the Kalman Filter and Extended Kalman Filter to hybrid dynamical systems. Away from hybrid events, the SKF is a standard Kalman filter. When a hybrid event occurs, the saltation matrix plays an analogous role as that of the system dynamics, subsequently inducing a discrete modification to both the prediction and update steps. Simulation results from the SKF show a reduced mean squared error in state estimation compared to using the differential of the reset map, especially immediately after a hybrid transition event.