The Uncertainty Aware Salted Kalman Filter: State Estimation for Hybrid Systems with Uncertain Guards
Paper and Code
Feb 25, 2022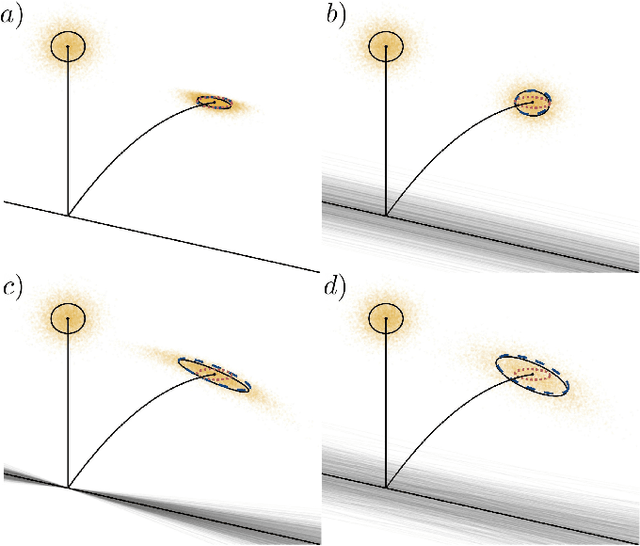
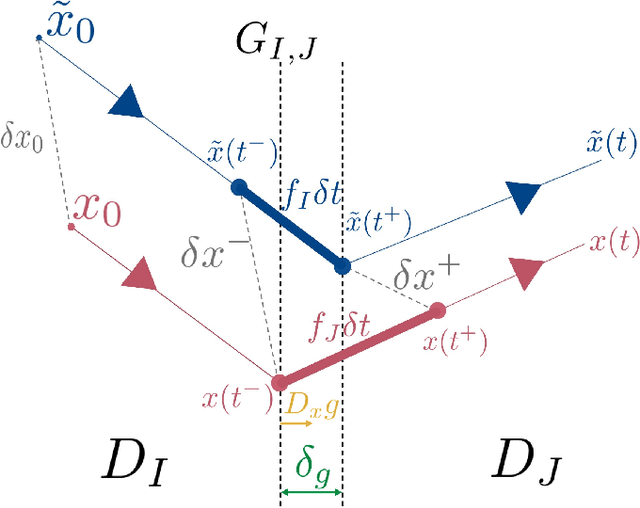
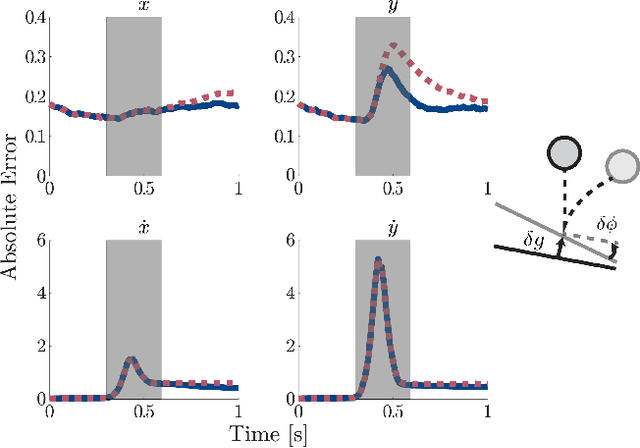
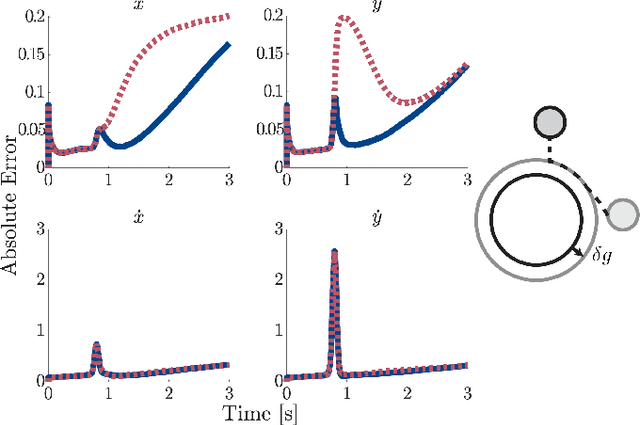
In this paper we present a method for updating robotic state belief through contact with uncertain surfaces and apply this update to a Kalman filter for more accurate state estimation. Examining how guard surface uncertainty affects the time spent in each mode, we derive a guard saltation matrix - which maps perturbations prior to hybrid events to perturbations after - accounting for additional variation in the resulting state. Additionally, we propose the use of parameterized reset functions - capturing how unknown parameters change how states are mapped from one mode to the next - the Jacobian of which accounts for the additional uncertainty in the resulting state. The accuracy of these mappings is shown by simulating sampled distributions through uncertain transition events and comparing the resulting covariances. Finally, we integrate these additional terms into the "uncertainty aware Salted Kalman Filter", uaSKF, and show a peak reduction in average estimation error by 24-60% on a variety of test conditions and systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge