Hybrid iLQR Model Predictive Control for Contact Implicit Stabilization on Legged Robots

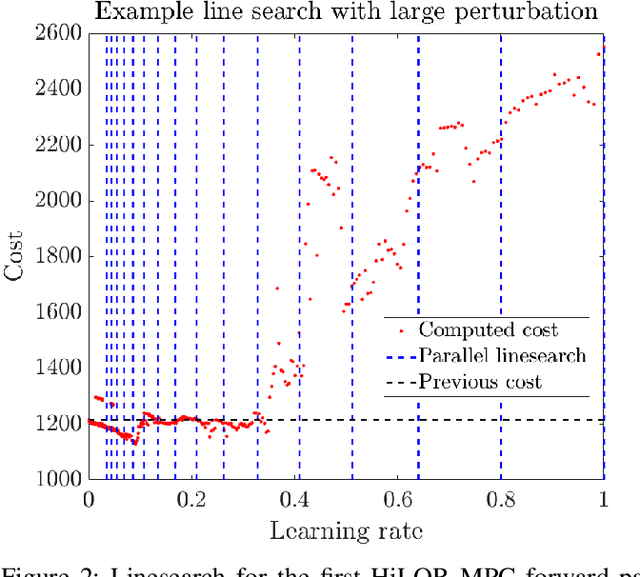
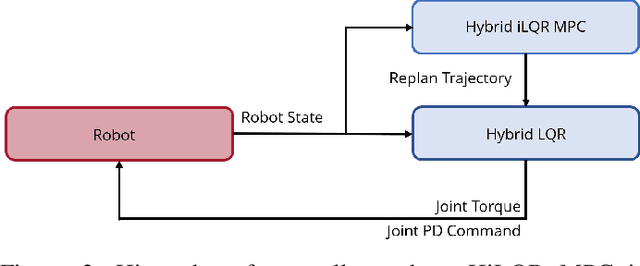
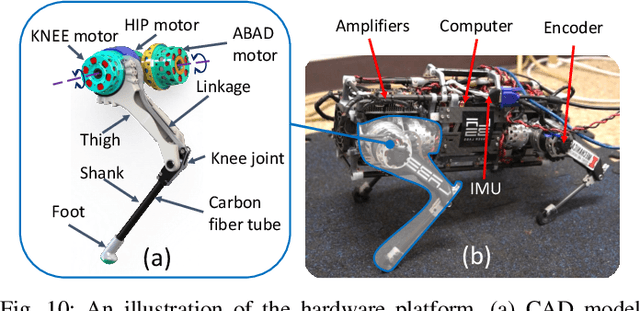
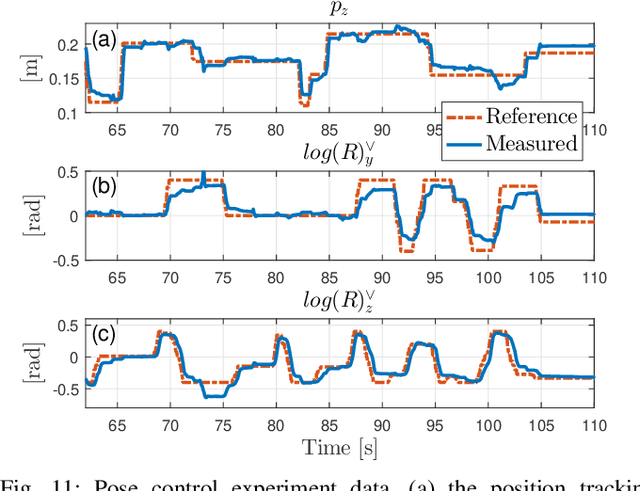
Model Predictive Control (MPC) is a popular strategy for controlling robots but is difficult for systems with contact due to the complex nature of hybrid dynamics. To implement MPC for systems with contact, dynamic models are often simplified or contact sequences fixed in time in order to plan trajectories efficiently. In this work, we extend Hybrid iterative Linear Quadratic Regulator to work in a MPC fashion (HiLQR MPC) by 1) modifying how the cost function is computed when contact modes do not align, 2) utilizing parallelizations when simulating rigid body dynamics, and 3) using efficient analytical derivative computations of the rigid body dynamics. The result is a system that can modify the contact sequence of the reference behavior and plan whole body motions cohesively -- which is crucial when dealing with large perturbations. HiLQR MPC is tested on two systems: first, the hybrid cost modification is validated on a simple actuated bouncing ball hybrid system. Then HiLQR MPC is compared against methods that utilize centroidal dynamic assumptions on a quadruped robot (Unitree A1). HiLQR MPC outperforms the centroidal methods in both simulation and hardware tests.

Representation-Free Model Predictive Control for Dynamic Motions in Quadrupeds

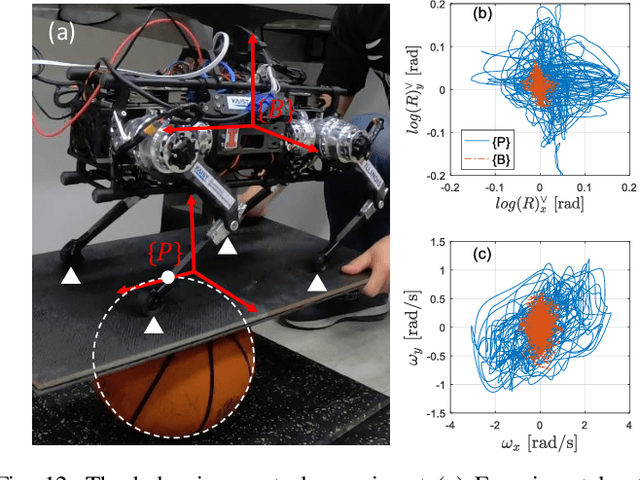
This paper presents a novel Representation-Free Model Predictive Control (RF-MPC) framework for controlling various dynamic motions of a quadrupedal robot in three dimensional (3D) space. Our formulation directly represents the rotational dynamics using the rotation matrix, which liberates us from the issues associated with the use of Euler angles and quaternion as the orientation representations. With a variation-based linearization scheme and a carefully constructed cost function, the MPC control law is transcribed to the standard Quadratic Program (QP) form. The MPC controller can operate at real-time rates of 250 Hz on a quadruped robot. Experimental results including periodic quadrupedal gaits and a controlled backflip validate that our control strategy could stabilize dynamic motions that involve singularity in 3D maneuvers.

Kinodynamic Motion Planning for Multi-Legged Robot Jumping via Mixed-Integer Convex Program

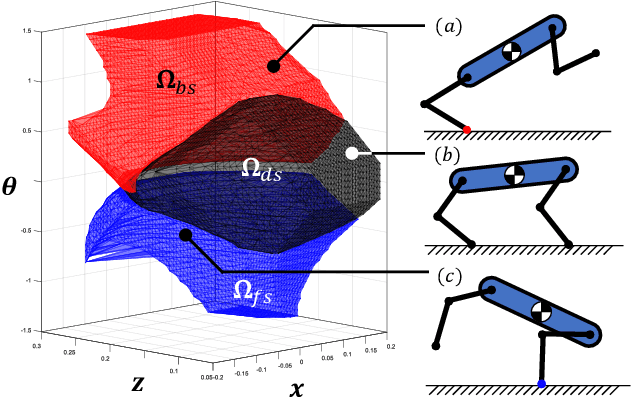
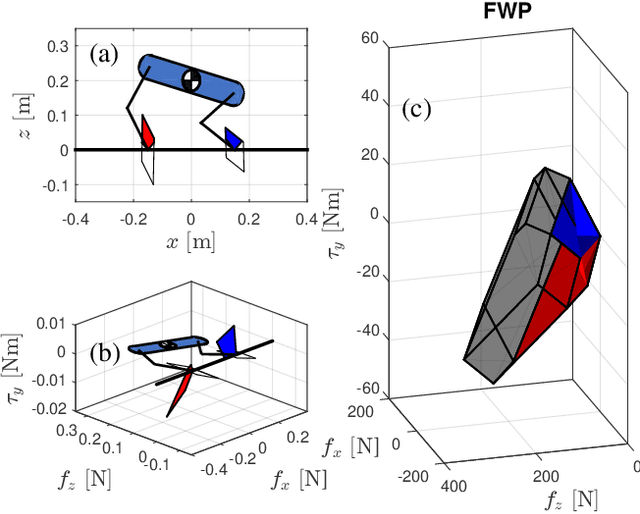
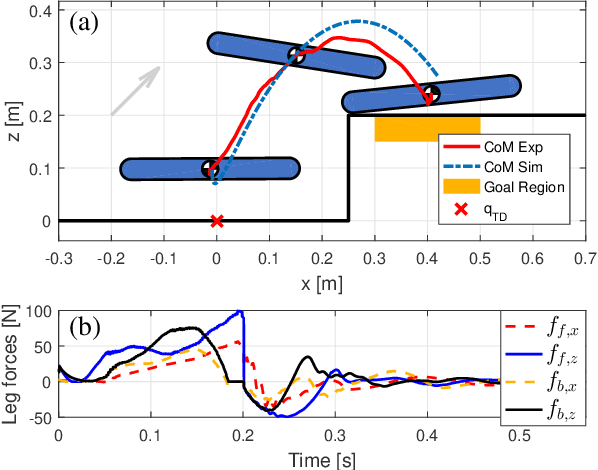
This paper proposes a kinodynamic motion planning framework for multi-legged robot jumping based on the mixed-integer convex program (MICP), which simultaneously reasons about centroidal motion, contact points, wrench, and gait sequences. This method uniquely combines configuration space discretization and the construction of feasible wrench polytope (FWP) to encode kinematic constraints, actuator limit, friction cone constraint, and gait sequencing into a single MICP. The MICP could be efficiently solved to the global optimum by off-the-shelf numerical solvers and provide highly dynamic jumping motions without requiring initial guesses. Simulation and experimental results demonstrate that the proposed method could find novel and dexterous maneuvers that are directly deployable on the two-legged robot platform to traverse through challenging terrains.