Kinodynamic Motion Planning for Multi-Legged Robot Jumping via Mixed-Integer Convex Program
Paper and Code
Nov 03, 2020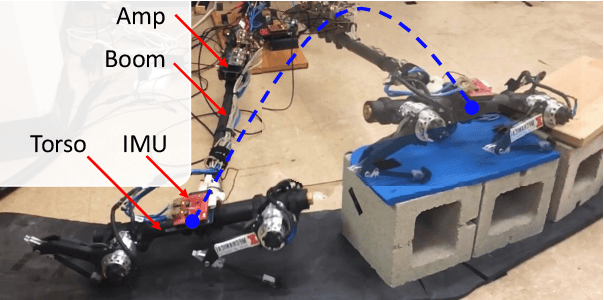
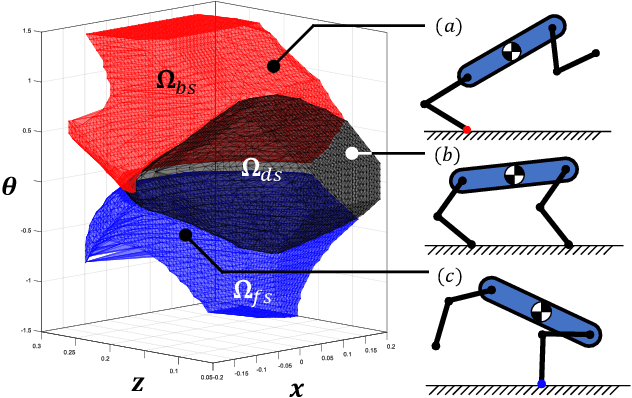
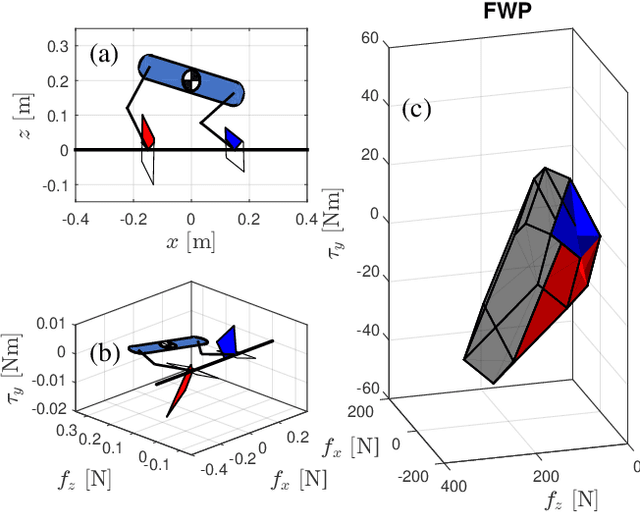
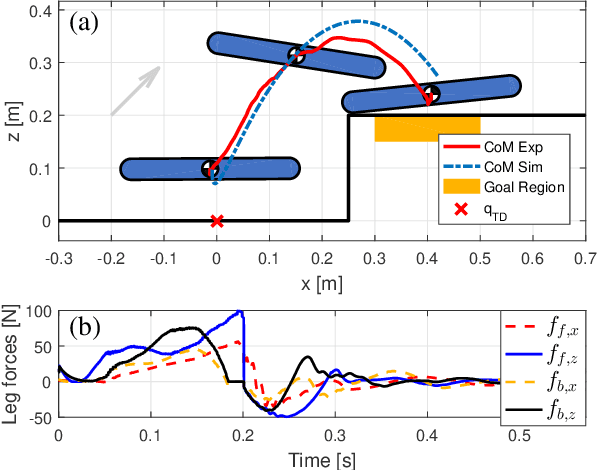
This paper proposes a kinodynamic motion planning framework for multi-legged robot jumping based on the mixed-integer convex program (MICP), which simultaneously reasons about centroidal motion, contact points, wrench, and gait sequences. This method uniquely combines configuration space discretization and the construction of feasible wrench polytope (FWP) to encode kinematic constraints, actuator limit, friction cone constraint, and gait sequencing into a single MICP. The MICP could be efficiently solved to the global optimum by off-the-shelf numerical solvers and provide highly dynamic jumping motions without requiring initial guesses. Simulation and experimental results demonstrate that the proposed method could find novel and dexterous maneuvers that are directly deployable on the two-legged robot platform to traverse through challenging terrains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge