Why do autoencoders work?

Deep neural network autoencoders are routinely used computationally for model reduction. They allow recognizing the intrinsic dimension of data that lie in a $k$-dimensional subset $K$ of an input Euclidean space $\mathbb{R}^n$. The underlying idea is to obtain both an encoding layer that maps $\mathbb{R}^n$ into $\mathbb{R}^k$ (called the bottleneck layer or the space of latent variables) and a decoding layer that maps $\mathbb{R}^k$ back into $\mathbb{R}^n$, in such a way that the input data from the set $K$ is recovered when composing the two maps. This is achieved by adjusting parameters (weights) in the network to minimize the discrepancy between the input and the reconstructed output. Since neural networks (with continuous activation functions) compute continuous maps, the existence of a network that achieves perfect reconstruction would imply that $K$ is homeomorphic to a $k$-dimensional subset of $\mathbb{R}^k$, so clearly there are topological obstructions to finding such a network. On the other hand, in practice the technique is found to "work" well, which leads one to ask if there is a way to explain this effectiveness. We show that, up to small errors, indeed the method is guaranteed to work. This is done by appealing to certain facts from differential geometry. A computational example is also included to illustrate the ideas.

A Compositional Approach to Certifying the Almost Global Asymptotic Stability of Cascade Systems

In this work, we give sufficient conditions for the almost global asymptotic stability of a cascade in which the inner loop and the unforced outer loop are each almost globally asymptotically stable. Our qualitative approach relies on the absence of chain recurrence for non-equilibrium points of the unforced outer loop, the hyperbolicity of equilibria, and the precompactness of forward trajectories. The result is extended inductively to upper triangular systems with an arbitrary number of subsystems. We show that the required structure of the chain recurrent set can be readily verified, and describe two important classes of systems with this property. We also show that the precompactness requirement can be verified by growth rate conditions on the interconnection term coupling the subsystems. Our results stand in contrast to prior works that require either global asymptotic stability of the subsystems (impossible for smooth systems evolving on general manifolds), time scale separation between the subsystems, or strong disturbance robustness properties of the outer loop. The approach has clear applications in stability certification of cascaded controllers for systems evolving on manifolds.

The Role of Symmetry in Constructing Geometric Flat Outputs for Free-Flying Robotic Systems

Mechanical systems naturally evolve on principal bundles describing their inherent symmetries. The ensuing factorization of the configuration manifold into a symmetry group and an internal shape space has provided deep insights into the locomotion of many robotic and biological systems. On the other hand, the property of differential flatness has enabled efficient, effective planning and control algorithms for various robotic systems. Yet, a practical means of finding a flat output for an arbitrary robotic system remains an open question. In this work, we demonstrate surprising new connections between these two domains, for the first time employing symmetry directly to construct a flat output. We provide sufficient conditions for the existence of a trivialization of the bundle in which the group variables themselves are a flat output. We call this a geometric flat output, since it is equivariant (i.e. maintains the symmetry) and is often global or almost-global, properties not typically enjoyed by other flat outputs. In such a trivialization, the motion planning problem is easily solved, since a given trajectory for the group variables will fully determine the trajectory for the shape variables that exactly achieves this motion. We provide a partial catalog of robotic systems with geometric flat outputs and worked examples for the planar rocket, planar aerial manipulator, and quadrotor.

Poincaré-Hopf theorem for hybrid systems

A generalization of the Poincar\'{e}-Hopf index theorem applicable to hybrid dynamical systems is obtained. For the hybrid systems considered, guard sets are not assumed to be smooth; distinct "modes" are not assumed to have constant dimension; and resets are arbitrary multivalued maps (relations).

Necessary conditions for feedback stabilization and safety

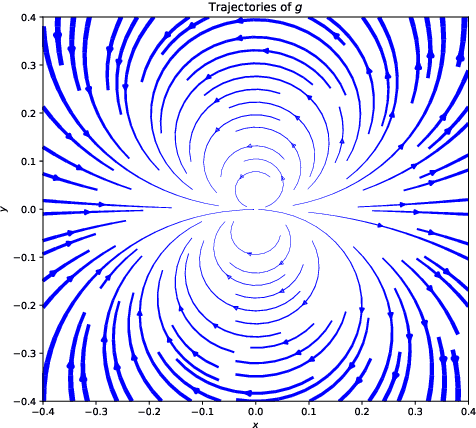
Brockett's necessary condition yields a test to determine whether a system can be made to stabilize about some operating point via continuous, purely state-dependent feedback. For many real-world systems, however, one wants to stabilize sets which are more general than a single point. One also wants to control such systems to operate safely by making obstacles and other "dangerous" sets repelling. We generalize Brockett's necessary condition to the case of stabilizing general compact subsets having a nonzero Euler characteristic. Using this generalization, we also formulate a necessary condition for the existence of "safe" control laws. We illustrate the theory in concrete examples and for some general classes of systems including a broad class of nonholonomically constrained Lagrangian systems. We also show that, for the special case of stabilizing a point, the specialization of our general stabilizability test is stronger than Brockett's.

Conley's fundamental theorem for a class of hybrid systems

We establish versions of Conley's (i) fundamental theorem and (ii) decomposition theorem for a broad class of hybrid dynamical systems. The hybrid version of (i) asserts that a globally-defined "hybrid complete Lyapunov function" exists for every hybrid system in this class. Motivated by mechanics and control settings where physical or engineered events cause abrupt changes in a system's governing dynamics, our results apply to a large class of Lagrangian hybrid systems (with impacts) studied extensively in the robotics literature. Viewed formally, these results generalize those of Conley and Franks for continuous-time and discrete-time dynamical systems, respectively, on metric spaces. However, we furnish specific examples illustrating how our statement of sufficient conditions represents merely an early step in the longer project of establishing what formal assumptions can and cannot endow hybrid systems models with the topologically well characterized partitions of limit behavior that make Conley's theory so valuable in those classical settings.

Gait modeling and optimization for the perturbed Stokes regime

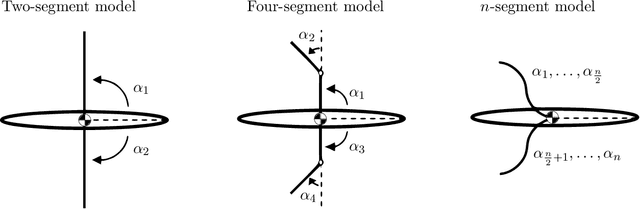
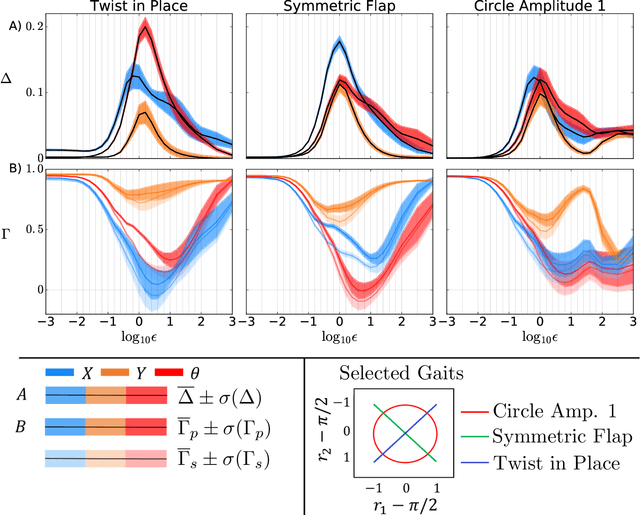
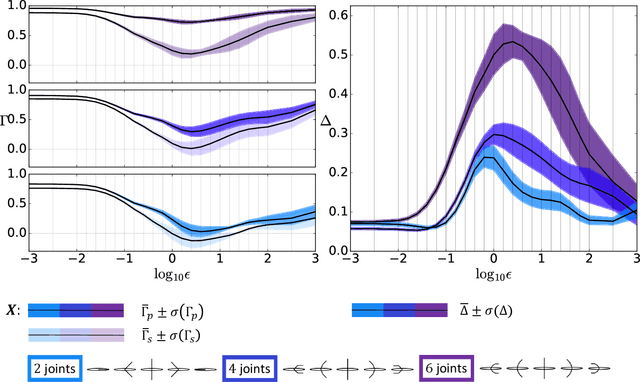
Many forms of locomotion, both natural and artificial, are dominated by viscous friction in the sense that without power expenditure they quickly come to a standstill. From geometric mechanics, it is known that for swimming at the "Stokesian" (viscous; zero Reynolds number) limit, the motion is governed by a reduced order "connection" model that describes how body shape change produces motion for the body frame with respect to the world. In the "perturbed Stokes regime" where inertial forces are still dominated by viscosity, but are not negligible (low Reynolds number), we show that motion is still governed by a functional relationship between shape velocity and body velocity, but this function is no longer linear in shape change rate. We derive this model using results from singular perturbation theory, and the theory of noncompact normally hyperbolic invariant manifolds (NHIMs). Using the theoretical properties of this reduced-order model, we develop an algorithm that estimates an approximation to the dynamics near a cyclic body shape change (a "gait") directly from observational data of shape and body motion. This extends our previous work which assumed kinematic "connection" models. To compare the old and new algorithms, we analyze simulated swimmers over a range of inertia to damping ratios. Our new class of models performs well on the Stokesian regime, and over several orders of magnitude outside it into the perturbed Stokes regime, where it gives significantly improved prediction accuracy compared to previous work. In addition to algorithmic improvements, we thereby present a new class of models that is of independent interest. Their application to data-driven modeling improves our ability to study the optimality of animal gaits, and our ability to use hardware-in-the-loop optimization to produce gaits for robots.