Generative Planning with Fast Collision Checks for High Speed Navigation

Reasoning about large numbers of diverse plans to achieve high speed navigation in cluttered environments remains a challenge for robotic systems even in the case of perfect perceptual information. Often, this is tackled by methods that iteratively optimize around a prior seeded trajectory and consequently restrict to local optima. We present a novel planning method using normalizing flows (NFs) to encode expert-styled motion primitives. We also present an accelerated collision checking framework that enables rejecting samples from the prior distribution before running them through the NF model for rapid sampling of collision-free trajectories. The choice of an NF as the generator permits a flexible way to encode diverse multi-modal behavior distributions while maintaining a smooth relation to the input space which allows approximating collision checks on NF inputs rather than outputs. We show comparable performance to model predictive path integral control in random cluttered environments and improved exit rates in a cul-de-sac environment. We conclude by discussing our plans for future work to improve both safety and performance of our controller.

Optimizing Gait Libraries via a Coverage Metric

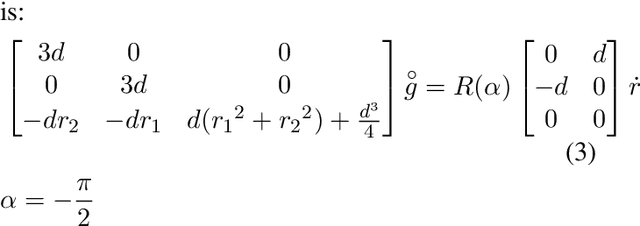
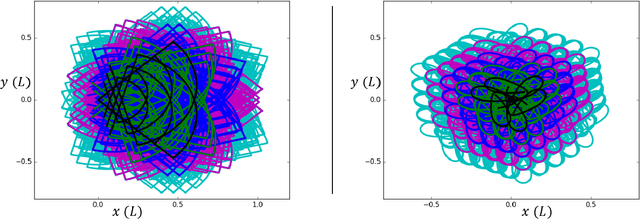
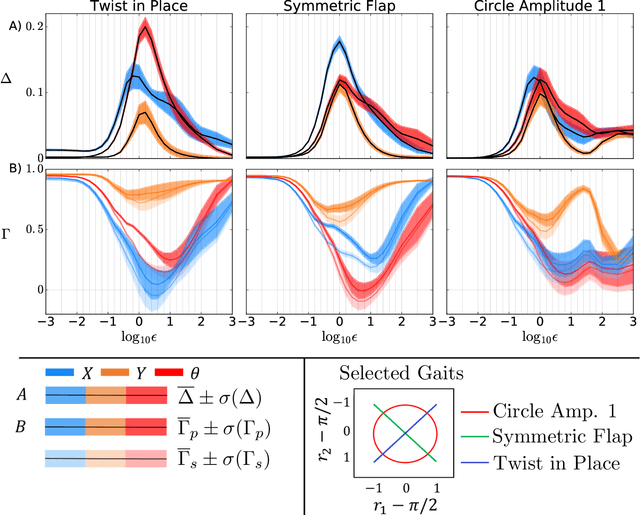
Many robots move through the world by composing locomotion primitives like steps and turns. To do so well, robots need not have primitives that make intuitive sense to humans. This becomes of paramount importance when robots are damaged and no longer move as designed. Here we propose a goal function we call "coverage", that represents the usefulness of a library of locomotion primitives in a manner agnostic to the particulars of the primitives themselves. We demonstrate the ability to optimize coverage on both simulated and physical robots, and show that coverage can be rapidly recovered after injury. This suggests that by optimizing for coverage, robots can sustain their ability to navigate through the world even in the face of significant mechanical failures. The benefits of this approach are enhanced by sample-efficient, data-driven approaches to system identification that can rapidly inform the optimization of primitives. We found that the number of degrees of freedom improved the rate of recovery of our simulated robots, a rare result in the fields of gait optimization and reinforcement learning. We showed that a robot with limbs made of tree branches (for which no CAD model or first principles model was available) is able to quickly find an effective high-coverage library of motion primitives. The optimized primitives are entirely non-obvious to a human observer, and thus are unlikely to be attainable through manual tuning.

Data-Driven Geometric System Identification for Shape-Underactuated Dissipative Systems

The study of systems whose movement is both geometric and dissipative offers an opportunity to quickly both identify models and optimize motion. Here, the geometry indicates reduction of the dynamics by environmental homogeneity while the dissipative nature minimizes the role of second order (inertial) features in the dynamics. In this work, we extend the tools of geometric system identification to "Shape-Underactuated Dissipative Systems (SUDS)" -- systems whose motions are kinematic, but whose actuation is restricted to a subset of the body shape coordinates. A large class of SUDS includes highly damped robots with series elastic actuators, and many soft robots. We validate the predictive quality of the models using simulations of a variety of viscous swimming systems. For a large class of SUDS, we show how the shape velocity actuation inputs can be directly converted into torque inputs suggesting that, e.g., systems with soft pneumatic actuators or dielectric elastomers, could be controlled in this way. Based on fundamental assumptions in the physics, we show how our model complexity scales linearly with the number of passive shape coordinates. This offers a large reduction on the number of trials needed to identify the system model from experimental data, and may reduce overfitting. The sample efficiency of our method suggests its use in modeling, control, and optimization in robotics, and as a tool for the study of organismal motion in friction dominated regimes.

Gait modeling and optimization for the perturbed Stokes regime

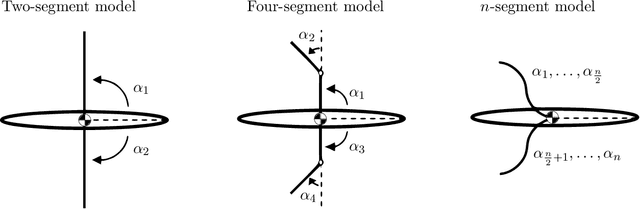
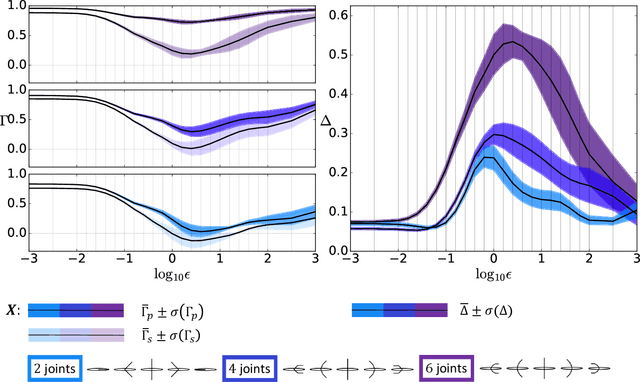
Many forms of locomotion, both natural and artificial, are dominated by viscous friction in the sense that without power expenditure they quickly come to a standstill. From geometric mechanics, it is known that for swimming at the "Stokesian" (viscous; zero Reynolds number) limit, the motion is governed by a reduced order "connection" model that describes how body shape change produces motion for the body frame with respect to the world. In the "perturbed Stokes regime" where inertial forces are still dominated by viscosity, but are not negligible (low Reynolds number), we show that motion is still governed by a functional relationship between shape velocity and body velocity, but this function is no longer linear in shape change rate. We derive this model using results from singular perturbation theory, and the theory of noncompact normally hyperbolic invariant manifolds (NHIMs). Using the theoretical properties of this reduced-order model, we develop an algorithm that estimates an approximation to the dynamics near a cyclic body shape change (a "gait") directly from observational data of shape and body motion. This extends our previous work which assumed kinematic "connection" models. To compare the old and new algorithms, we analyze simulated swimmers over a range of inertia to damping ratios. Our new class of models performs well on the Stokesian regime, and over several orders of magnitude outside it into the perturbed Stokes regime, where it gives significantly improved prediction accuracy compared to previous work. In addition to algorithmic improvements, we thereby present a new class of models that is of independent interest. Their application to data-driven modeling improves our ability to study the optimality of animal gaits, and our ability to use hardware-in-the-loop optimization to produce gaits for robots.