Gait modeling and optimization for the perturbed Stokes regime

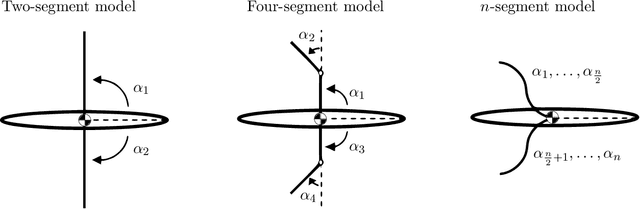
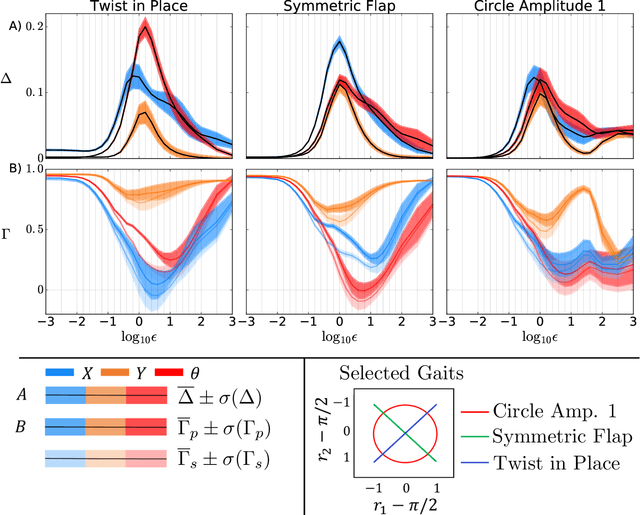
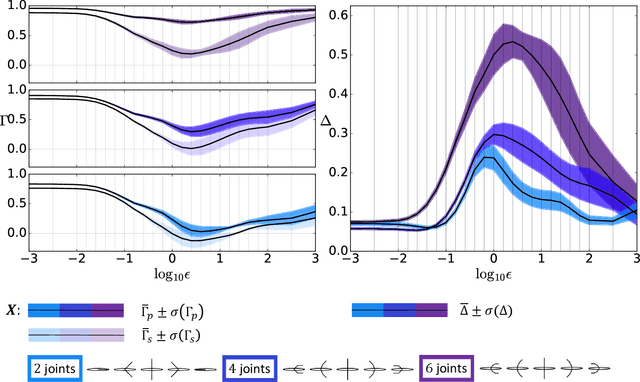
Many forms of locomotion, both natural and artificial, are dominated by viscous friction in the sense that without power expenditure they quickly come to a standstill. From geometric mechanics, it is known that for swimming at the "Stokesian" (viscous; zero Reynolds number) limit, the motion is governed by a reduced order "connection" model that describes how body shape change produces motion for the body frame with respect to the world. In the "perturbed Stokes regime" where inertial forces are still dominated by viscosity, but are not negligible (low Reynolds number), we show that motion is still governed by a functional relationship between shape velocity and body velocity, but this function is no longer linear in shape change rate. We derive this model using results from singular perturbation theory, and the theory of noncompact normally hyperbolic invariant manifolds (NHIMs). Using the theoretical properties of this reduced-order model, we develop an algorithm that estimates an approximation to the dynamics near a cyclic body shape change (a "gait") directly from observational data of shape and body motion. This extends our previous work which assumed kinematic "connection" models. To compare the old and new algorithms, we analyze simulated swimmers over a range of inertia to damping ratios. Our new class of models performs well on the Stokesian regime, and over several orders of magnitude outside it into the perturbed Stokes regime, where it gives significantly improved prediction accuracy compared to previous work. In addition to algorithmic improvements, we thereby present a new class of models that is of independent interest. Their application to data-driven modeling improves our ability to study the optimality of animal gaits, and our ability to use hardware-in-the-loop optimization to produce gaits for robots.