Satish V. Ukkusuri
Data Mining in Transportation Networks with Graph Neural Networks: A Review and Outlook
Jan 28, 2025



Abstract:Data mining in transportation networks (DMTNs) refers to using diverse types of spatio-temporal data for various transportation tasks, including pattern analysis, traffic prediction, and traffic controls. Graph neural networks (GNNs) are essential in many DMTN problems due to their capability to represent spatial correlations between entities. Between 2016 and 2024, the notable applications of GNNs in DMTNs have extended to multiple fields such as traffic prediction and operation. However, existing reviews have primarily focused on traffic prediction tasks. To fill this gap, this study provides a timely and insightful summary of GNNs in DMTNs, highlighting new progress in prediction and operation from academic and industry perspectives since 2023. First, we present and analyze various DMTN problems, followed by classical and recent GNN models. Second, we delve into key works in three areas: (1) traffic prediction, (2) traffic operation, and (3) industry involvement, such as Google Maps, Amap, and Baidu Maps. Along these directions, we discuss new research opportunities based on the significance of transportation problems and data availability. Finally, we compile resources such as data, code, and other learning materials to foster interdisciplinary communication. This review, driven by recent trends in GNNs in DMTN studies since 2023, could democratize abundant datasets and efficient GNN methods for various transportation problems including prediction and operation.
Mean-Field Control based Approximation of Multi-Agent Reinforcement Learning in Presence of a Non-decomposable Shared Global State
Jan 13, 2023
Abstract:Mean Field Control (MFC) is a powerful approximation tool to solve large-scale Multi-Agent Reinforcement Learning (MARL) problems. However, the success of MFC relies on the presumption that given the local states and actions of all the agents, the next (local) states of the agents evolve conditionally independent of each other. Here we demonstrate that even in a MARL setting where agents share a common global state in addition to their local states evolving conditionally independently (thus introducing a correlation between the state transition processes of individual agents), the MFC can still be applied as a good approximation tool. The global state is assumed to be non-decomposable i.e., it cannot be expressed as a collection of local states of the agents. We compute the approximation error as $\mathcal{O}(e)$ where $e=\frac{1}{\sqrt{N}}\left[\sqrt{|\mathcal{X}|} +\sqrt{|\mathcal{U}|}\right]$. The size of the agent population is denoted by the term $N$, and $|\mathcal{X}|, |\mathcal{U}|$ respectively indicate the sizes of (local) state and action spaces of individual agents. The approximation error is found to be independent of the size of the shared global state space. We further demonstrate that in a special case if the reward and state transition functions are independent of the action distribution of the population, then the error can be improved to $e=\frac{\sqrt{|\mathcal{X}|}}{\sqrt{N}}$. Finally, we devise a Natural Policy Gradient based algorithm that solves the MFC problem with $\mathcal{O}(\epsilon^{-3})$ sample complexity and obtains a policy that is within $\mathcal{O}(\max\{e,\epsilon\})$ error of the optimal MARL policy for any $\epsilon>0$.
Mean-Field Approximation of Cooperative Constrained Multi-Agent Reinforcement Learning (CMARL)
Sep 15, 2022
Abstract:Mean-Field Control (MFC) has recently been proven to be a scalable tool to approximately solve large-scale multi-agent reinforcement learning (MARL) problems. However, these studies are typically limited to unconstrained cumulative reward maximization framework. In this paper, we show that one can use the MFC approach to approximate the MARL problem even in the presence of constraints. Specifically, we prove that, an $N$-agent constrained MARL problem, with state, and action spaces of each individual agents being of sizes $|\mathcal{X}|$, and $|\mathcal{U}|$ respectively, can be approximated by an associated constrained MFC problem with an error, $e\triangleq \mathcal{O}\left([\sqrt{|\mathcal{X}|}+\sqrt{|\mathcal{U}|}]/\sqrt{N}\right)$. In a special case where the reward, cost, and state transition functions are independent of the action distribution of the population, we prove that the error can be improved to $e=\mathcal{O}(\sqrt{|\mathcal{X}|}/\sqrt{N})$. Also, we provide a Natural Policy Gradient based algorithm and prove that it can solve the constrained MARL problem within an error of $\mathcal{O}(e)$ with a sample complexity of $\mathcal{O}(e^{-6})$.
On the Near-Optimality of Local Policies in Large Cooperative Multi-Agent Reinforcement Learning
Sep 07, 2022
Abstract:We show that in a cooperative $N$-agent network, one can design locally executable policies for the agents such that the resulting discounted sum of average rewards (value) well approximates the optimal value computed over all (including non-local) policies. Specifically, we prove that, if $|\mathcal{X}|, |\mathcal{U}|$ denote the size of state, and action spaces of individual agents, then for sufficiently small discount factor, the approximation error is given by $\mathcal{O}(e)$ where $e\triangleq \frac{1}{\sqrt{N}}\left[\sqrt{|\mathcal{X}|}+\sqrt{|\mathcal{U}|}\right]$. Moreover, in a special case where the reward and state transition functions are independent of the action distribution of the population, the error improves to $\mathcal{O}(e)$ where $e\triangleq \frac{1}{\sqrt{N}}\sqrt{|\mathcal{X}|}$. Finally, we also devise an algorithm to explicitly construct a local policy. With the help of our approximation results, we further establish that the constructed local policy is within $\mathcal{O}(\max\{e,\epsilon\})$ distance of the optimal policy, and the sample complexity to achieve such a local policy is $\mathcal{O}(\epsilon^{-3})$, for any $\epsilon>0$.
Can Mean Field Control (MFC) Approximate Cooperative Multi Agent Reinforcement Learning (MARL) with Non-Uniform Interaction?
Feb 28, 2022

Abstract:Mean-Field Control (MFC) is a powerful tool to solve Multi-Agent Reinforcement Learning (MARL) problems. Recent studies have shown that MFC can well-approximate MARL when the population size is large and the agents are exchangeable. Unfortunately, the presumption of exchangeability implies that all agents uniformly interact with one another which is not true in many practical scenarios. In this article, we relax the assumption of exchangeability and model the interaction between agents via an arbitrary doubly stochastic matrix. As a result, in our framework, the mean-field `seen' by different agents are different. We prove that, if the reward of each agent is an affine function of the mean-field seen by that agent, then one can approximate such a non-uniform MARL problem via its associated MFC problem within an error of $e=\mathcal{O}(\frac{1}{\sqrt{N}}[\sqrt{|\mathcal{X}|} + \sqrt{|\mathcal{U}|}])$ where $N$ is the population size and $|\mathcal{X}|$, $|\mathcal{U}|$ are the sizes of state and action spaces respectively. Finally, we develop a Natural Policy Gradient (NPG) algorithm that can provide a solution to the non-uniform MARL with an error $\mathcal{O}(\max\{e,\epsilon\})$ and a sample complexity of $\mathcal{O}(\epsilon^{-3})$ for any $\epsilon >0$.
Deep Learning based Coverage and Rate Manifold Estimation in Cellular Networks
Feb 13, 2022
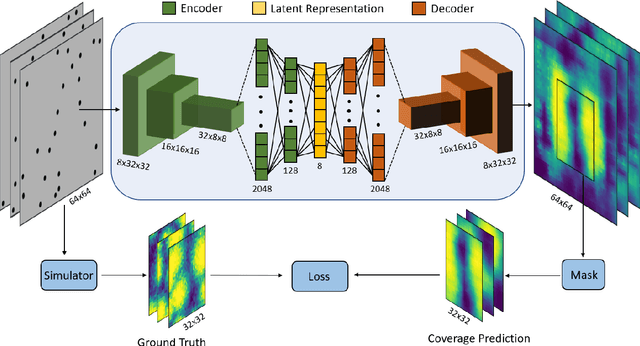

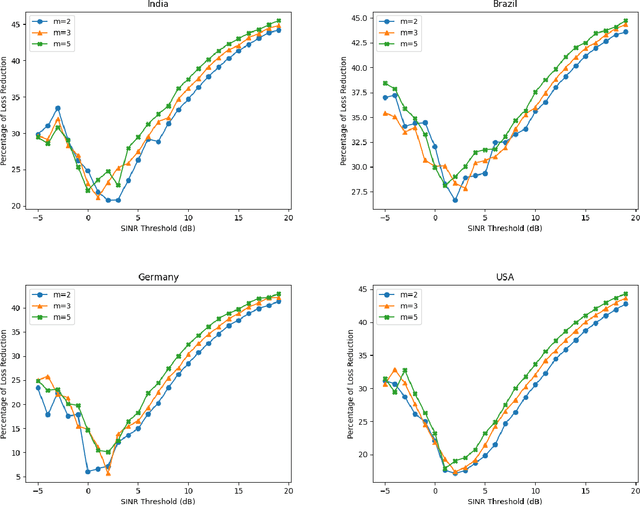
Abstract:This article proposes Convolutional Neural Network-based Auto Encoder (CNN-AE) to predict location-dependent rate and coverage probability of a network from its topology. We train the CNN utilising BS location data of India, Brazil, Germany, and the USA and compare its performance with stochastic geometry (SG) based analytical models. In comparison to the best-fitted SG-based model, CNN-AE improves the coverage and rate prediction errors by a margin of as large as $40\%$ and $25\%$ respectively. As an application, we propose a low complexity, provably convergent algorithm that, using trained CNN-AE, can compute locations of new BSs that need to be deployed in a network in order to satisfy pre-defined spatially heterogeneous performance goals.
On the Approximation of Cooperative Heterogeneous Multi-Agent Reinforcement Learning (MARL) using Mean Field Control (MFC)
Sep 09, 2021Abstract:Mean field control (MFC) is an effective way to mitigate the curse of dimensionality of cooperative multi-agent reinforcement learning (MARL) problems. This work considers a collection of $N_{\mathrm{pop}}$ heterogeneous agents that can be segregated into $K$ classes such that the $k$-th class contains $N_k$ homogeneous agents. We aim to prove approximation guarantees of the MARL problem for this heterogeneous system by its corresponding MFC problem. We consider three scenarios where the reward and transition dynamics of all agents are respectively taken to be functions of $(1)$ joint state and action distributions across all classes, $(2)$ individual distributions of each class, and $(3)$ marginal distributions of the entire population. We show that, in these cases, the $K$-class MARL problem can be approximated by MFC with errors given as $e_1=\mathcal{O}(\frac{\sqrt{|\mathcal{X}||\mathcal{U}|}}{N_{\mathrm{pop}}}\sum_{k}\sqrt{N_k})$, $e_2=\mathcal{O}(\sqrt{|\mathcal{X}||\mathcal{U}|}\sum_{k}\frac{1}{\sqrt{N_k}})$ and $e_3=\mathcal{O}\left(\sqrt{|\mathcal{X}||\mathcal{U}|}\left[\frac{A}{N_{\mathrm{pop}}}\sum_{k\in[K]}\sqrt{N_k}+\frac{B}{\sqrt{N_{\mathrm{pop}}}}\right]\right)$, respectively, where $A, B$ are some constants and $|\mathcal{X}|,|\mathcal{U}|$ are the sizes of state and action spaces of each agent. Finally, we design a Natural Policy Gradient (NPG) based algorithm that, in the three cases stated above, can converge to an optimal MARL policy within $\mathcal{O}(e_j)$ error with a sample complexity of $\mathcal{O}(e_j^{-3})$, $j\in\{1,2,3\}$, respectively.
Quantifying spatial homogeneity of urban road networks via graph neural networks
Jan 01, 2021

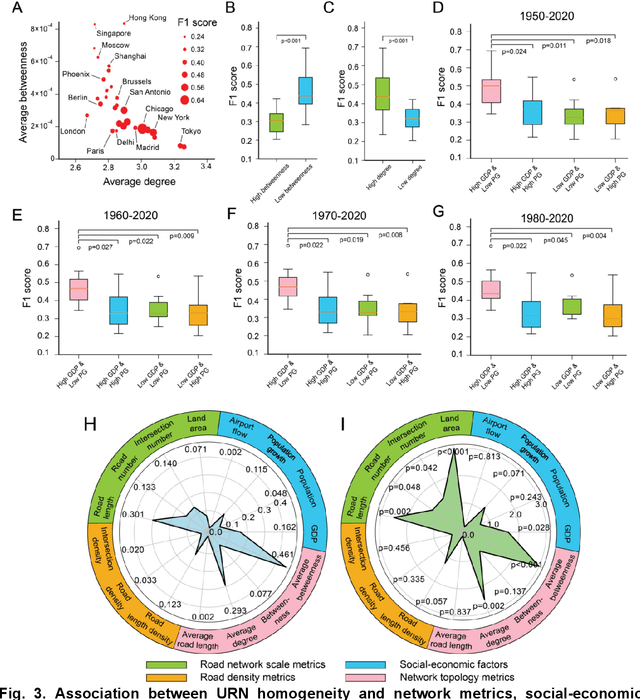
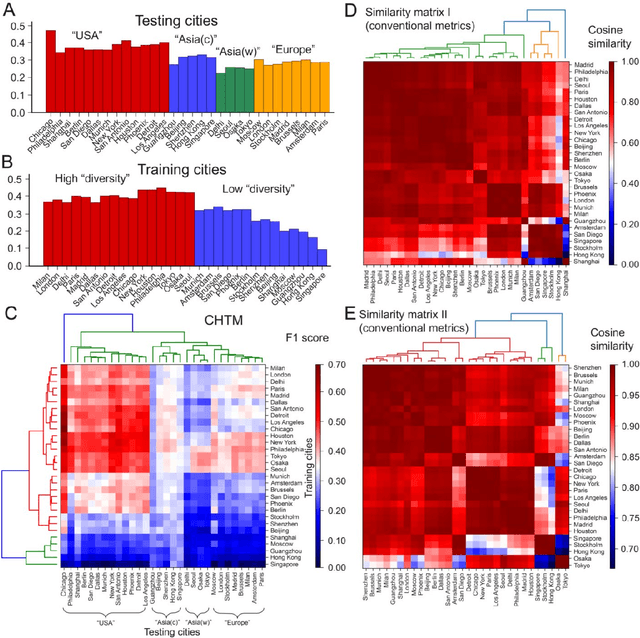
Abstract:The spatial homogeneity of an urban road network (URN) measures whether each distinct component is analogous to the whole network and can serve as a quantitative manner bridging network structure and dynamics. However, given the complexity of cities, it is challenging to quantify spatial homogeneity simply based on conventional network statistics. In this work, we use Graph Neural Networks to model the 11,790 URN samples across 30 cities worldwide and use its predictability to define the spatial homogeneity. The proposed measurement can be viewed as a non-linear integration of multiple geometric properties, such as degree, betweenness, road network type, and a strong indicator of mixed socio-economic events, such as GDP and population growth. City clusters derived from transferring spatial homogeneity can be interpreted well by continental urbanization histories. We expect this novel metric supports various subsequent tasks in transportation, urban planning, and geography.
City2City: Translating Place Representations across Cities
Nov 26, 2019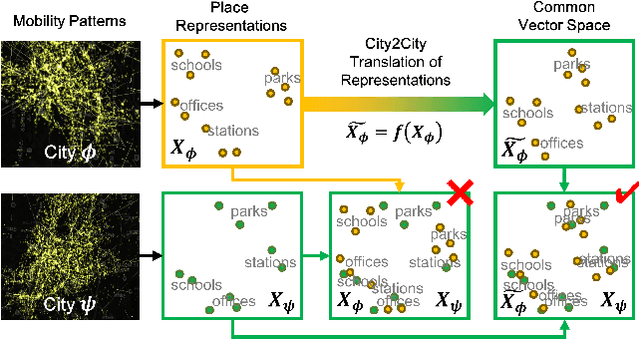
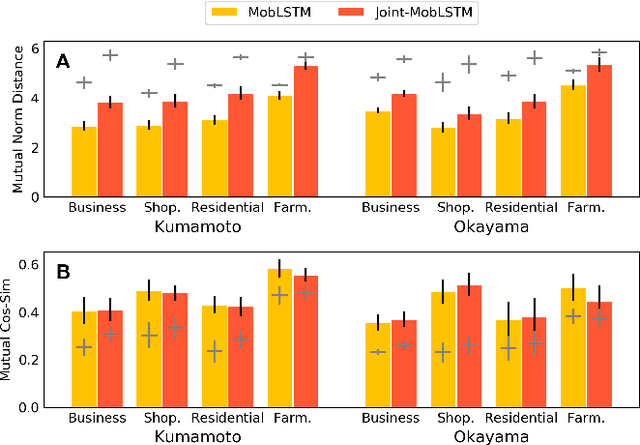
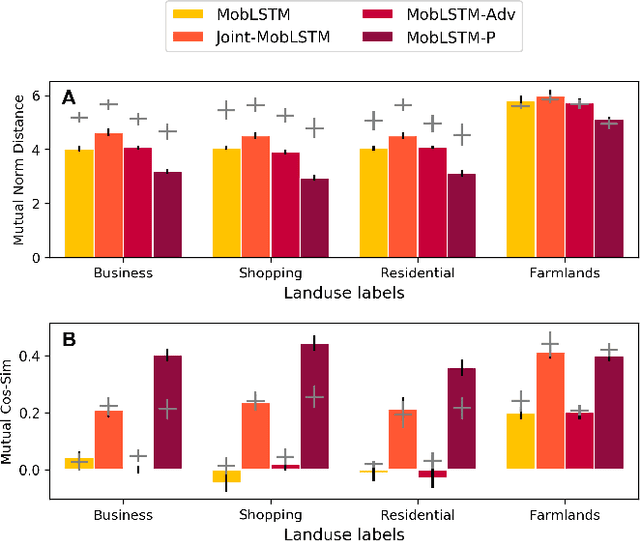
Abstract:Large mobility datasets collected from various sources have allowed us to observe, analyze, predict and solve a wide range of important urban challenges. In particular, studies have generated place representations (or embeddings) from mobility patterns in a similar manner to word embeddings to better understand the functionality of different places within a city. However, studies have been limited to generating such representations of cities in an individual manner and has lacked an inter-city perspective, which has made it difficult to transfer the insights gained from the place representations across different cities. In this study, we attempt to bridge this research gap by treating \textit{cities} and \textit{languages} analogously. We apply methods developed for unsupervised machine language translation tasks to translate place representations across different cities. Real world mobility data collected from mobile phone users in 2 cities in Japan are used to test our place representation translation methods. Translated place representations are validated using landuse data, and results show that our methods were able to accurately translate place representations from one city to another.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge