Spectral Clustering via Orthogonalization-Free Methods

Graph Signal Filter used as dimensionality reduction in spectral clustering usually requires expensive eigenvalue estimation. We analyze the filter in an optimization setting and propose to use four orthogonalization-free methods by optimizing objective functions as dimensionality reduction in spectral clustering. The proposed methods do not utilize any orthogonalization, which is known as not well scalable in a parallel computing environment. Our methods theoretically construct adequate feature space, which is, at most, a weighted alteration to the eigenspace of a normalized Laplacian matrix. We numerically hypothesize that the proposed methods are equivalent in clustering quality to the ideal Graph Signal Filter, which exploits the exact eigenvalue needed without expensive eigenvalue estimation. Numerical results show that the proposed methods outperform Power Iteration-based methods and Graph Signal Filter in clustering quality and computation cost. Unlike Power Iteration-based methods and Graph Signal Filter which require random signal input, our methods are able to utilize available initialization in the streaming graph scenarios. Additionally, numerical results show that our methods outperform ARPACK and are faster than LOBPCG in the streaming graph scenarios. We also present numerical results showing the scalability of our methods in multithreading and multiprocessing implementations to facilitate parallel spectral clustering.

A Distributed Block Chebyshev-Davidson Algorithm for Parallel Spectral Clustering

We develop a distributed Block Chebyshev-Davidson algorithm to solve large-scale leading eigenvalue problems for spectral analysis in spectral clustering. First, the efficiency of the Chebyshev-Davidson algorithm relies on the prior knowledge of the eigenvalue spectrum, which could be expensive to estimate. This issue can be lessened by the analytic spectrum estimation of the Laplacian or normalized Laplacian matrices in spectral clustering, making the proposed algorithm very efficient for spectral clustering. Second, to make the proposed algorithm capable of analyzing big data, a distributed and parallel version has been developed with attractive scalability. The speedup by parallel computing is approximately equivalent to $\sqrt{p}$, where $p$ denotes the number of processes. Numerical results will be provided to demonstrate its efficiency and advantage over existing algorithms in both sequential and parallel computing.

Quantifying spatial homogeneity of urban road networks via graph neural networks

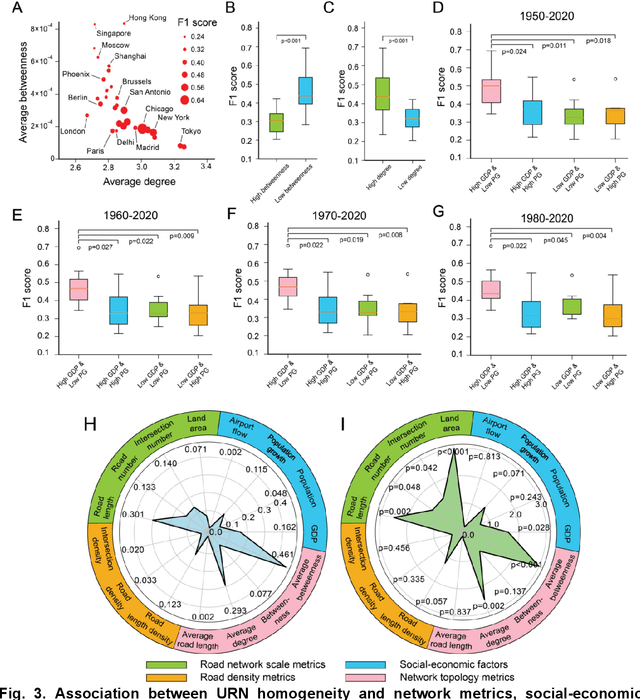
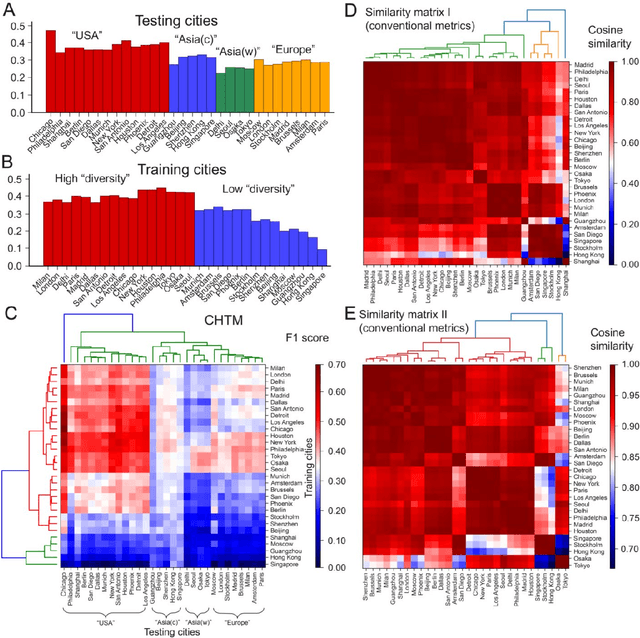
The spatial homogeneity of an urban road network (URN) measures whether each distinct component is analogous to the whole network and can serve as a quantitative manner bridging network structure and dynamics. However, given the complexity of cities, it is challenging to quantify spatial homogeneity simply based on conventional network statistics. In this work, we use Graph Neural Networks to model the 11,790 URN samples across 30 cities worldwide and use its predictability to define the spatial homogeneity. The proposed measurement can be viewed as a non-linear integration of multiple geometric properties, such as degree, betweenness, road network type, and a strong indicator of mixed socio-economic events, such as GDP and population growth. City clusters derived from transferring spatial homogeneity can be interpreted well by continental urbanization histories. We expect this novel metric supports various subsequent tasks in transportation, urban planning, and geography.