VaR\ and CVaR Estimation in a Markov Cost Process: Lower and Upper Bounds

We tackle the problem of estimating the Value-at-Risk (VaR) and the Conditional Value-at-Risk (CVaR) of the infinite-horizon discounted cost within a Markov cost process. First, we derive a minimax lower bound of $\Omega(1/\sqrt{n})$ that holds both in an expected and in a probabilistic sense. Then, using a finite-horizon truncation scheme, we derive an upper bound for the error in CVaR estimation, which matches our lower bound up to constant factors. Finally, we discuss an extension of our estimation scheme that covers more general risk measures satisfying a certain continuity criterion, e.g., spectral risk measures, utility-based shortfall risk. To the best of our knowledge, our work is the first to provide lower and upper bounds on the estimation error for any risk measure within Markovian settings. We remark that our lower bounds also extend to the infinite-horizon discounted costs' mean. Even in that case, our result $\Omega(1/\sqrt{n}) $ improves upon the existing result $\Omega(1/n)$[13].

Learning to Liquidate Forex: Optimal Stopping via Adaptive Top-K Regression

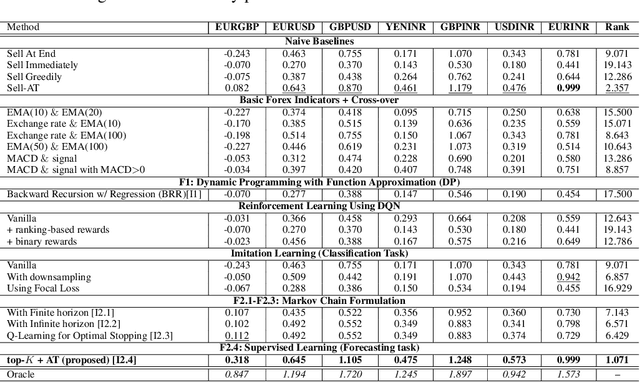
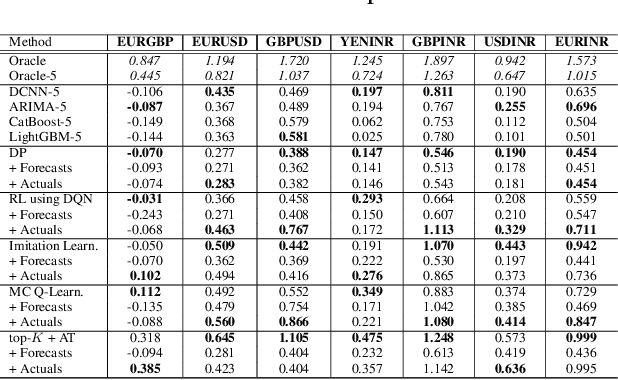
We consider learning a trading agent acting on behalf of the treasury of a firm earning revenue in a foreign currency (FC) and incurring expenses in the home currency (HC). The goal of the agent is to maximize the expected HC at the end of the trading episode by deciding to hold or sell the FC at each time step in the trading episode. We pose this as an optimization problem, and consider a broad spectrum of approaches with the learning component ranging from supervised to imitation to reinforcement learning. We observe that most of the approaches considered struggle to improve upon simple heuristic baselines. We identify two key aspects of the problem that render standard solutions ineffective - i) while good forecasts of future FX rates can be highly effective in guiding good decisions, forecasting FX rates is difficult, and erroneous estimates tend to degrade the performance of trading agents instead of improving it, ii) the inherent non-stationary nature of FX rates renders a fixed decision-threshold highly ineffective. To address these problems, we propose a novel supervised learning approach that learns to forecast the top-K future FX rates instead of forecasting all the future FX rates, and bases the hold-versus-sell decision on the forecasts (e.g. hold if future FX rate is higher than current FX rate, sell otherwise). Furthermore, to handle the non-stationarity in the FX rates data which poses challenges to the i.i.d. assumption in supervised learning methods, we propose to adaptively learn decision-thresholds based on recent historical episodes. Through extensive empirical evaluation, we show that our approach is the only approach which is able to consistently improve upon a simple heuristic baseline. Further experiments show the inefficacy of state-of-the-art statistical and deep-learning-based forecasting methods as they degrade the performance of the trading agent.

Electricity Consumption Forecasting for Out-of-distribution Time-of-Use Tariffs

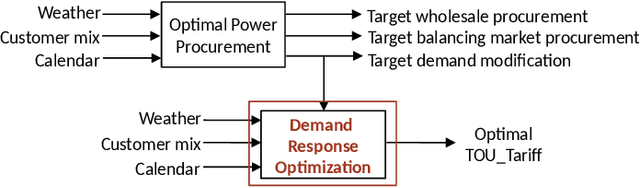
In electricity markets, retailers or brokers want to maximize profits by allocating tariff profiles to end consumers. One of the objectives of such demand response management is to incentivize the consumers to adjust their consumption so that the overall electricity procurement in the wholesale markets is minimized, e.g. it is desirable that consumers consume less during peak hours when cost of procurement for brokers from wholesale markets are high. We consider a greedy solution to maximize the overall profit for brokers by optimal tariff profile allocation. This in-turn requires forecasting electricity consumption for each user for all tariff profiles. This forecasting problem is challenging compared to standard forecasting problems due to following reasons: i. the number of possible combinations of hourly tariffs is high and retailers may not have considered all combinations in the past resulting in a biased set of tariff profiles tried in the past, ii. the profiles allocated in the past to each user is typically based on certain policy. These reasons violate the standard i.i.d. assumptions, as there is a need to evaluate new tariff profiles on existing customers and historical data is biased by the policies used in the past for tariff allocation. In this work, we consider several scenarios for forecasting and optimization under these conditions. We leverage the underlying structure of how consumers respond to variable tariff rates by comparing tariffs across hours and shifting loads, and propose suitable inductive biases in the design of deep neural network based architectures for forecasting under such scenarios. More specifically, we leverage attention mechanisms and permutation equivariant networks that allow desirable processing of tariff profiles to learn tariff representations that are insensitive to the biases in the data and still representative of the task.