Hyper: Hyperparameter Robust Efficient Exploration in Reinforcement Learning

The exploration \& exploitation dilemma poses significant challenges in reinforcement learning (RL). Recently, curiosity-based exploration methods achieved great success in tackling hard-exploration problems. However, they necessitate extensive hyperparameter tuning on different environments, which heavily limits the applicability and accessibility of this line of methods. In this paper, we characterize this problem via analysis of the agent behavior, concluding the fundamental difficulty of choosing a proper hyperparameter. We then identify the difficulty and the instability of the optimization when the agent learns with curiosity. We propose our method, hyperparameter robust exploration (\textbf{Hyper}), which extensively mitigates the problem by effectively regularizing the visitation of the exploration and decoupling the exploitation to ensure stable training. We theoretically justify that \textbf{Hyper} is provably efficient under function approximation setting and empirically demonstrate its appealing performance and robustness in various environments.

Scaling Distributed Multi-task Reinforcement Learning with Experience Sharing

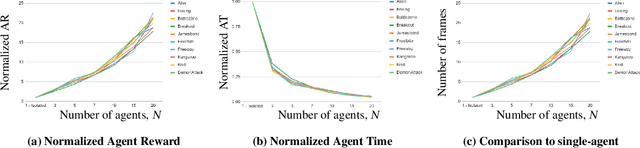
Recently, DARPA launched the ShELL program, which aims to explore how experience sharing can benefit distributed lifelong learning agents in adapting to new challenges. In this paper, we address this issue by conducting both theoretical and empirical research on distributed multi-task reinforcement learning (RL), where a group of $N$ agents collaboratively solves $M$ tasks without prior knowledge of their identities. We approach the problem by formulating it as linearly parameterized contextual Markov decision processes (MDPs), where each task is represented by a context that specifies the transition dynamics and rewards. To tackle this problem, we propose an algorithm called DistMT-LSVI. First, the agents identify the tasks, and then they exchange information through a central server to derive $\epsilon$-optimal policies for the tasks. Our research demonstrates that to achieve $\epsilon$-optimal policies for all $M$ tasks, a single agent using DistMT-LSVI needs to run a total number of episodes that is at most $\tilde{\mathcal{O}}({d^3H^6(\epsilon^{-2}+c_{\rm sep}^{-2})}\cdot M/N)$, where $c_{\rm sep}>0$ is a constant representing task separability, $H$ is the horizon of each episode, and $d$ is the feature dimension of the dynamics and rewards. Notably, DistMT-LSVI improves the sample complexity of non-distributed settings by a factor of $1/N$, as each agent independently learns $\epsilon$-optimal policies for all $M$ tasks using $\tilde{\mathcal{O}}(d^3H^6M\epsilon^{-2})$ episodes. Additionally, we provide numerical experiments conducted on OpenAI Gym Atari environments that validate our theoretical findings.

Provably Efficient Lifelong Reinforcement Learning with Linear Function Approximation

We study lifelong reinforcement learning (RL) in a regret minimization setting of linear contextual Markov decision process (MDP), where the agent needs to learn a multi-task policy while solving a streaming sequence of tasks. We propose an algorithm, called UCB Lifelong Value Distillation (UCBlvd), that provably achieves sublinear regret for any sequence of tasks, which may be adaptively chosen based on the agent's past behaviors. Remarkably, our algorithm uses only sublinear number of planning calls, which means that the agent eventually learns a policy that is near optimal for multiple tasks (seen or unseen) without the need of deliberate planning. A key to this property is a new structural assumption that enables computation sharing across tasks during exploration. Specifically, for $K$ task episodes of horizon $H$, our algorithm has a regret bound $\tilde{\mathcal{O}}(\sqrt{(d^3+d^\prime d)H^4K})$ based on $\mathcal{O}(dH\log(K))$ number of planning calls, where $d$ and $d^\prime$ are the feature dimensions of the dynamics and rewards, respectively. This theoretical guarantee implies that our algorithm can enable a lifelong learning agent to accumulate experiences and learn to rapidly solve new tasks.

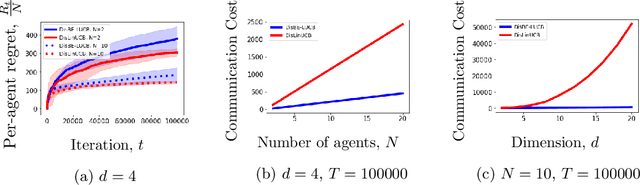
Distributed Contextual Linear Bandits with Minimax Optimal Communication Cost

We study distributed contextual linear bandits with stochastic contexts, where $N$ agents act cooperatively to solve a linear bandit-optimization problem with $d$-dimensional features. For this problem, we propose a distributed batch elimination version of the LinUCB algorithm, DisBE-LUCB, where the agents share information among each other through a central server. We prove that over $T$ rounds ($NT$ actions in total) the communication cost of DisBE-LUCB is only $\tilde{\mathcal{O}}(dN)$ and its regret is at most $\tilde{\mathcal{O}}(\sqrt{dNT})$, which is of the same order as that incurred by an optimal single-agent algorithm for $NT$ rounds. Remarkably, we derive an information-theoretic lower bound on the communication cost of the distributed contextual linear bandit problem with stochastic contexts, and prove that our proposed algorithm is nearly minimax optimal in terms of \emph{both regret and communication cost}. Finally, we propose DecBE-LUCB, a fully decentralized version of DisBE-LUCB, which operates without a central server, where agents share information with their \emph{immediate neighbors} through a carefully designed consensus procedure.

Safe Reinforcement Learning with Linear Function Approximation

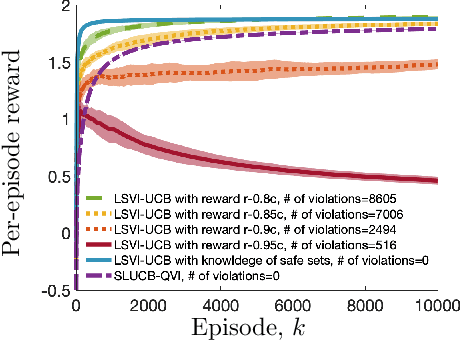
Safety in reinforcement learning has become increasingly important in recent years. Yet, existing solutions either fail to strictly avoid choosing unsafe actions, which may lead to catastrophic results in safety-critical systems, or fail to provide regret guarantees for settings where safety constraints need to be learned. In this paper, we address both problems by first modeling safety as an unknown linear cost function of states and actions, which must always fall below a certain threshold. We then present algorithms, termed SLUCB-QVI and RSLUCB-QVI, for episodic Markov decision processes (MDPs) with linear function approximation. We show that SLUCB-QVI and RSLUCB-QVI, while with \emph{no safety violation}, achieve a $\tilde{\mathcal{O}}\left(\kappa\sqrt{d^3H^3T}\right)$ regret, nearly matching that of state-of-the-art unsafe algorithms, where $H$ is the duration of each episode, $d$ is the dimension of the feature mapping, $\kappa$ is a constant characterizing the safety constraints, and $T$ is the total number of action plays. We further present numerical simulations that corroborate our theoretical findings.

UCB-based Algorithms for Multinomial Logistic Regression Bandits

Out of the rich family of generalized linear bandits, perhaps the most well studied ones are logisitc bandits that are used in problems with binary rewards: for instance, when the learner/agent tries to maximize the profit over a user that can select one of two possible outcomes (e.g., `click' vs `no-click'). Despite remarkable recent progress and improved algorithms for logistic bandits, existing works do not address practical situations where the number of outcomes that can be selected by the user is larger than two (e.g., `click', `show me later', `never show again', `no click'). In this paper, we study such an extension. We use multinomial logit (MNL) to model the probability of each one of $K+1\geq 2$ possible outcomes (+1 stands for the `not click' outcome): we assume that for a learner's action $\mathbf{x}_t$, the user selects one of $K+1\geq 2$ outcomes, say outcome $i$, with a multinomial logit (MNL) probabilistic model with corresponding unknown parameter $\bar{\boldsymbol\theta}_{\ast i}$. Each outcome $i$ is also associated with a revenue parameter $\rho_i$ and the goal is to maximize the expected revenue. For this problem, we present MNL-UCB, an upper confidence bound (UCB)-based algorithm, that achieves regret $\tilde{\mathcal{O}}(dK\sqrt{T})$ with small dependency on problem-dependent constants that can otherwise be arbitrarily large and lead to loose regret bounds. We present numerical simulations that corroborate our theoretical results.

Decentralized Multi-Agent Linear Bandits with Safety Constraints

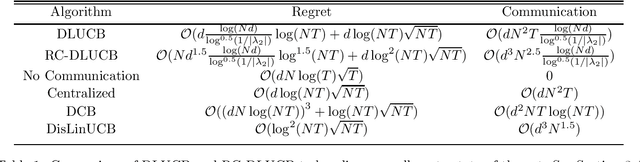
We study decentralized stochastic linear bandits, where a network of $N$ agents acts cooperatively to efficiently solve a linear bandit-optimization problem over a $d$-dimensional space. For this problem, we propose DLUCB: a fully decentralized algorithm that minimizes the cumulative regret over the entire network. At each round of the algorithm each agent chooses its actions following an upper confidence bound (UCB) strategy and agents share information with their immediate neighbors through a carefully designed consensus procedure that repeats over cycles. Our analysis adjusts the duration of these communication cycles ensuring near-optimal regret performance $\mathcal{O}(d\log{NT}\sqrt{NT})$ at a communication rate of $\mathcal{O}(dN^2)$ per round. The structure of the network affects the regret performance via a small additive term - coined the regret of delay - that depends on the spectral gap of the underlying graph. Notably, our results apply to arbitrary network topologies without a requirement for a dedicated agent acting as a server. In consideration of situations with high communication cost, we propose RC-DLUCB: a modification of DLUCB with rare communication among agents. The new algorithm trades off regret performance for a significantly reduced total communication cost of $\mathcal{O}(d^3N^{2.5})$ over all $T$ rounds. Finally, we show that our ideas extend naturally to the emerging, albeit more challenging, setting of safe bandits. For the recently studied problem of linear bandits with unknown linear safety constraints, we propose the first safe decentralized algorithm. Our study contributes towards applying bandit techniques in safety-critical distributed systems that repeatedly deal with unknown stochastic environments. We present numerical simulations for various network topologies that corroborate our theoretical findings.

Regret Bounds for Safe Gaussian Process Bandit Optimization

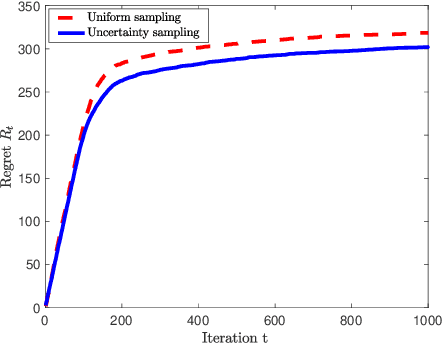
Many applications require a learner to make sequential decisions given uncertainty regarding both the system's payoff function and safety constraints. In safety-critical systems, it is paramount that the learner's actions do not violate the safety constraints at any stage of the learning process. In this paper, we study a stochastic bandit optimization problem where the unknown payoff and constraint functions are sampled from Gaussian Processes (GPs) first considered in [Srinivas et al., 2010]. We develop a safe variant of GP-UCB called SGP-UCB, with necessary modifications to respect safety constraints at every round. The algorithm has two distinct phases. The first phase seeks to estimate the set of safe actions in the decision set, while the second phase follows the GP-UCB decision rule. Our main contribution is to derive the first sub-linear regret bounds for this problem. We numerically compare SGP-UCB against existing safe Bayesian GP optimization algorithms.

Safe Linear Thompson Sampling

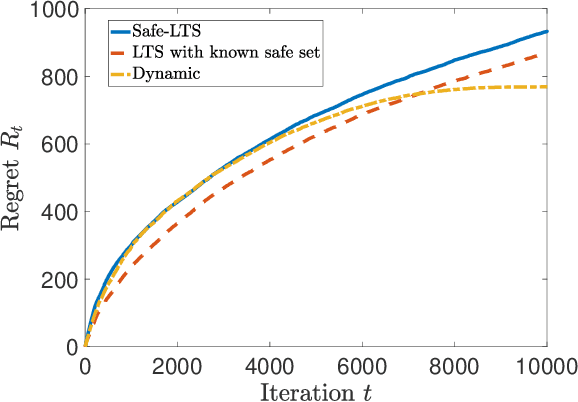
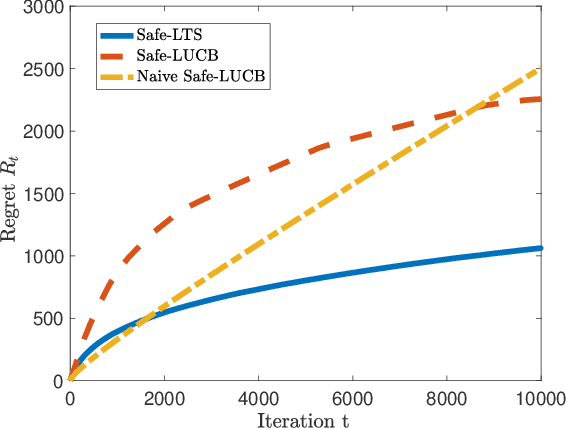
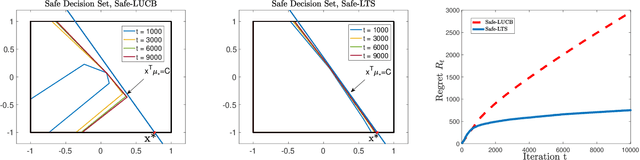
The design and performance analysis of bandit algorithms in the presence of stage-wise safety or reliability constraints has recently garnered significant interest. In this work, we consider the linear stochastic bandit problem under additional \textit{linear safety constraints} that need to be satisfied at each round. We provide a new safe algorithm based on linear Thompson Sampling (TS) for this problem and show a frequentist regret of order $\mathcal{O} (d^{3/2}\log^{1/2}d \cdot T^{1/2}\log^{3/2}T)$, which remarkably matches the results provided by [Abeille et al., 2017] for the standard linear TS algorithm in the absence of safety constraints. We compare the performance of our algorithm with a UCB-based safe algorithm and highlight how the inherently randomized nature of TS leads to a superior performance in expanding the set of safe actions the algorithm has access to at each round.

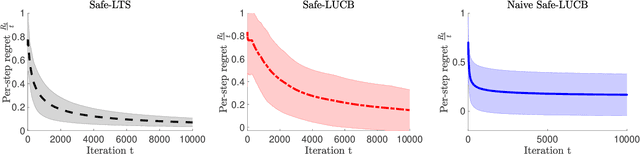
Linear Stochastic Bandits Under Safety Constraints

Bandit algorithms have various application in safety-critical systems, where it is important to respect the system constraints that rely on the bandit's unknown parameters at every round. In this paper, we formulate a linear stochastic multi-armed bandit problem with safety constraints that depend (linearly) on an unknown parameter vector. As such, the learner is unable to identify all safe actions and must act conservatively in ensuring that her actions satisfy the safety constraint at all rounds (at least with high probability). For these bandits, we propose a new UCB-based algorithm called Safe-LUCB, which includes necessary modifications to respect safety constraints. The algorithm has two phases. During the pure exploration phase the learner chooses her actions at random from a restricted set of safe actions with the goal of learning a good approximation of the entire unknown safe set. Once this goal is achieved, the algorithm begins a safe exploration-exploitation phase where the learner gradually expands their estimate of the set of safe actions while controlling the growth of regret. We provide a general regret bound for the algorithm, as well as a problem dependent bound that is connected to the location of the optimal action within the safe set. We then propose a modified heuristic that exploits our problem dependent analysis to improve the regret.