Safe Linear Thompson Sampling

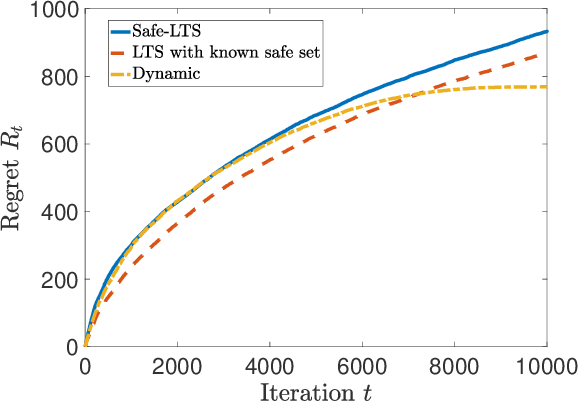
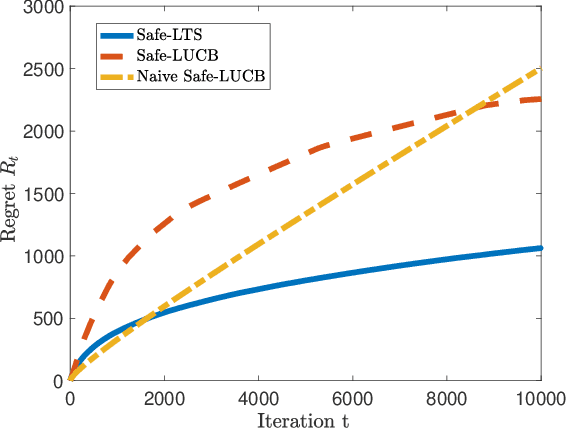
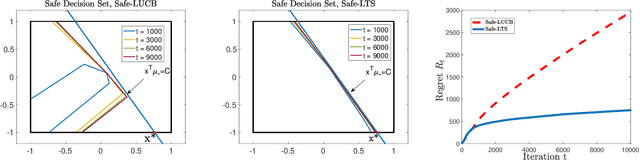
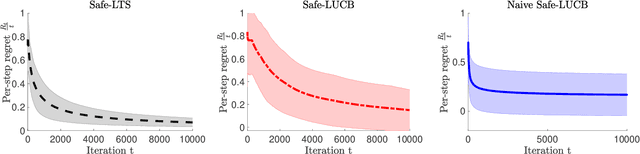
The design and performance analysis of bandit algorithms in the presence of stage-wise safety or reliability constraints has recently garnered significant interest. In this work, we consider the linear stochastic bandit problem under additional \textit{linear safety constraints} that need to be satisfied at each round. We provide a new safe algorithm based on linear Thompson Sampling (TS) for this problem and show a frequentist regret of order $\mathcal{O} (d^{3/2}\log^{1/2}d \cdot T^{1/2}\log^{3/2}T)$, which remarkably matches the results provided by [Abeille et al., 2017] for the standard linear TS algorithm in the absence of safety constraints. We compare the performance of our algorithm with a UCB-based safe algorithm and highlight how the inherently randomized nature of TS leads to a superior performance in expanding the set of safe actions the algorithm has access to at each round.