CompactifAI: Extreme Compression of Large Language Models using Quantum-Inspired Tensor Networks

Large Language Models (LLMs) such as ChatGPT and LlaMA are advancing rapidly in generative Artificial Intelligence (AI), but their immense size poses significant challenges, such as huge training and inference costs, substantial energy demands, and limitations for on-site deployment. Traditional compression methods such as pruning, distillation, and low-rank approximation focus on reducing the effective number of neurons in the network, while quantization focuses on reducing the numerical precision of individual weights to reduce the model size while keeping the number of neurons fixed. While these compression methods have been relatively successful in practice, there's no compelling reason to believe that truncating the number of neurons is an optimal strategy. In this context, this paper introduces CompactifAI, an innovative LLM compression approach using quantum-inspired Tensor Networks that focuses on the model's correlation space instead, allowing for a more controlled, refined and interpretable model compression. Our method is versatile and can be implemented with - or on top of - other compression techniques. As a benchmark, we demonstrate that CompactifAI alone enables compression of the LlaMA-2 7B model to only $30\%$ of its original size while recovering over $90\%$ of the original accuracy after a brief distributed retraining.

Boosting Defect Detection in Manufacturing using Tensor Convolutional Neural Networks

Defect detection is one of the most important yet challenging tasks in the quality control stage in the manufacturing sector. In this work, we introduce a Tensor Convolutional Neural Network (T-CNN) and examine its performance on a real defect detection application in one of the components of the ultrasonic sensors produced at Robert Bosch's manufacturing plants. Our quantum-inspired T-CNN operates on a reduced model parameter space to substantially improve the training speed and performance of an equivalent CNN model without sacrificing accuracy. More specifically, we demonstrate how T-CNNs are able to reach the same performance as classical CNNs as measured by quality metrics, with up to fifteen times fewer parameters and 4% to 19% faster training times. Our results demonstrate that the T-CNN greatly outperforms the results of traditional human visual inspection, providing value in a current real application in manufacturing.

Application of Tensor Neural Networks to Pricing Bermudan Swaptions

The Cheyette model is a quasi-Gaussian volatility interest rate model widely used to price interest rate derivatives such as European and Bermudan Swaptions for which Monte Carlo simulation has become the industry standard. In low dimensions, these approaches provide accurate and robust prices for European Swaptions but, even in this computationally simple setting, they are known to underestimate the value of Bermudan Swaptions when using the state variables as regressors. This is mainly due to the use of a finite number of predetermined basis functions in the regression. Moreover, in high-dimensional settings, these approaches succumb to the Curse of Dimensionality. To address these issues, Deep-learning techniques have been used to solve the backward Stochastic Differential Equation associated with the value process for European and Bermudan Swaptions; however, these methods are constrained by training time and memory. To overcome these limitations, we propose leveraging Tensor Neural Networks as they can provide significant parameter savings while attaining the same accuracy as classical Dense Neural Networks. In this paper we rigorously benchmark the performance of Tensor Neural Networks and Dense Neural Networks for pricing European and Bermudan Swaptions, and we show that Tensor Neural Networks can be trained faster than Dense Neural Networks and provide more accurate and robust prices than their Dense counterparts.

Quantum-Inspired Tensor Neural Networks for Option Pricing

Recent advances in deep learning have enabled us to address the curse of dimensionality (COD) by solving problems in higher dimensions. A subset of such approaches of addressing the COD has led us to solving high-dimensional PDEs. This has resulted in opening doors to solving a variety of real-world problems ranging from mathematical finance to stochastic control for industrial applications. Although feasible, these deep learning methods are still constrained by training time and memory. Tackling these shortcomings, Tensor Neural Networks (TNN) demonstrate that they can provide significant parameter savings while attaining the same accuracy as compared to the classical Dense Neural Network (DNN). In addition, we also show how TNN can be trained faster than DNN for the same accuracy. Besides TNN, we also introduce Tensor Network Initializer (TNN Init), a weight initialization scheme that leads to faster convergence with smaller variance for an equivalent parameter count as compared to a DNN. We benchmark TNN and TNN Init by applying them to solve the parabolic PDE associated with the Heston model, which is widely used in financial pricing theory.

Financial Risk Management on a Neutral Atom Quantum Processor

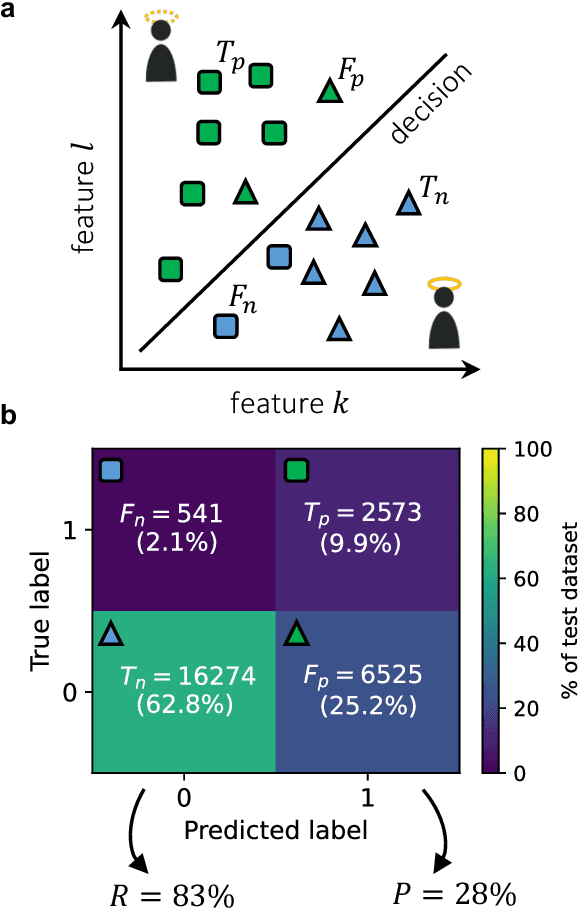
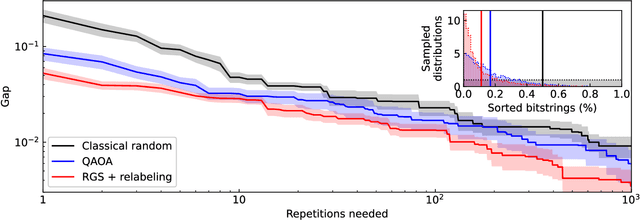
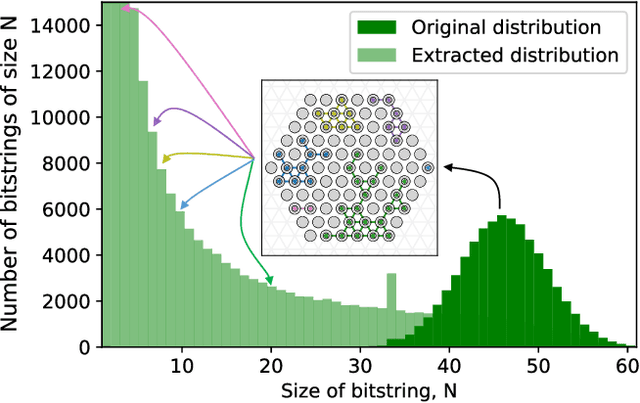
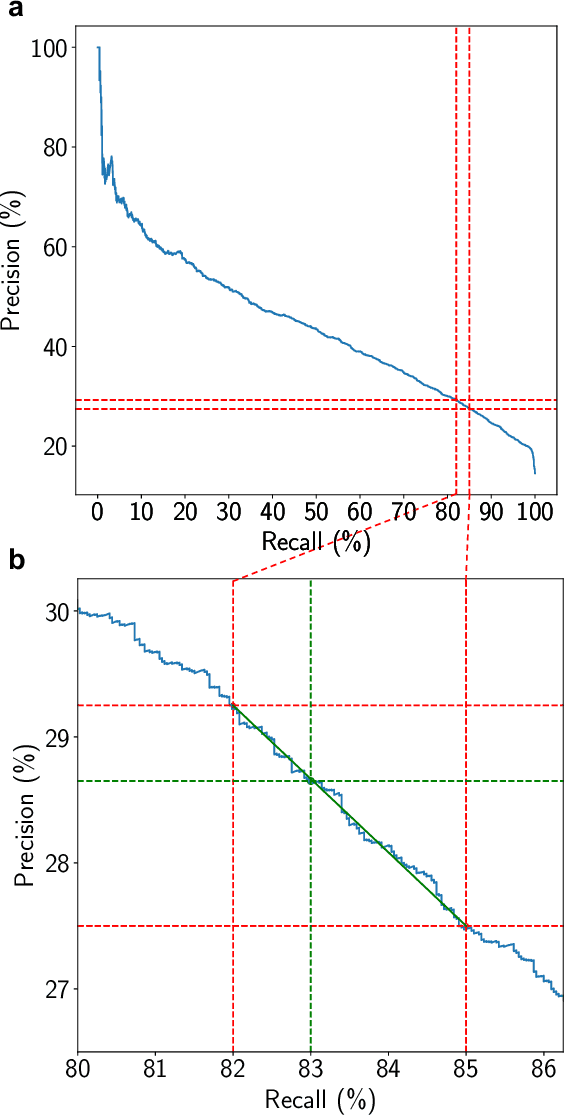
Machine Learning models capable of handling the large datasets collected in the financial world can often become black boxes expensive to run. The quantum computing paradigm suggests new optimization techniques, that combined with classical algorithms, may deliver competitive, faster and more interpretable models. In this work we propose a quantum-enhanced machine learning solution for the prediction of credit rating downgrades, also known as fallen-angels forecasting in the financial risk management field. We implement this solution on a neutral atom Quantum Processing Unit with up to 60 qubits on a real-life dataset. We report competitive performances against the state-of-the-art Random Forest benchmark whilst our model achieves better interpretability and comparable training times. We examine how to improve performance in the near-term validating our ideas with Tensor Networks-based numerical simulations.

Quantum-Inspired Tensor Neural Networks for Partial Differential Equations

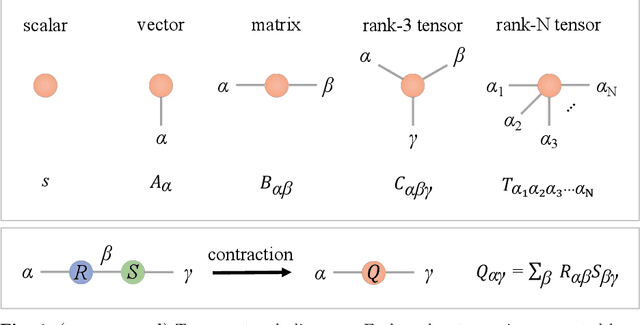
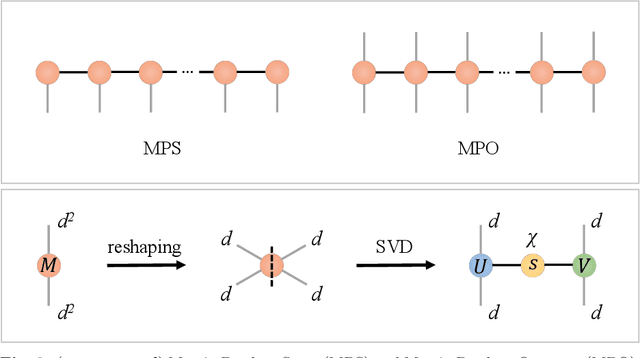
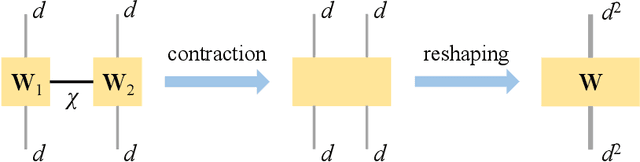
Partial Differential Equations (PDEs) are used to model a variety of dynamical systems in science and engineering. Recent advances in deep learning have enabled us to solve them in a higher dimension by addressing the curse of dimensionality in new ways. However, deep learning methods are constrained by training time and memory. To tackle these shortcomings, we implement Tensor Neural Networks (TNN), a quantum-inspired neural network architecture that leverages Tensor Network ideas to improve upon deep learning approaches. We demonstrate that TNN provide significant parameter savings while attaining the same accuracy as compared to the classical Dense Neural Network (DNN). In addition, we also show how TNN can be trained faster than DNN for the same accuracy. We benchmark TNN by applying them to solve parabolic PDEs, specifically the Black-Scholes-Barenblatt equation, widely used in financial pricing theory, empirically showing the advantages of TNN over DNN. Further examples, such as the Hamilton-Jacobi-Bellman equation, are also discussed.

Quantum artificial vision for defect detection in manufacturing

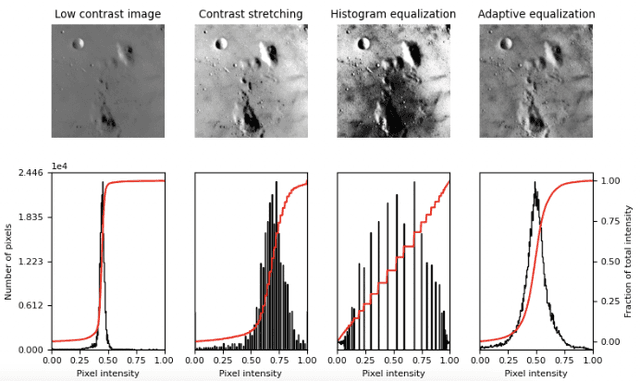
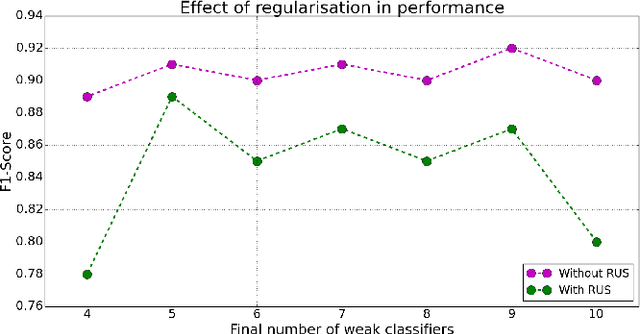
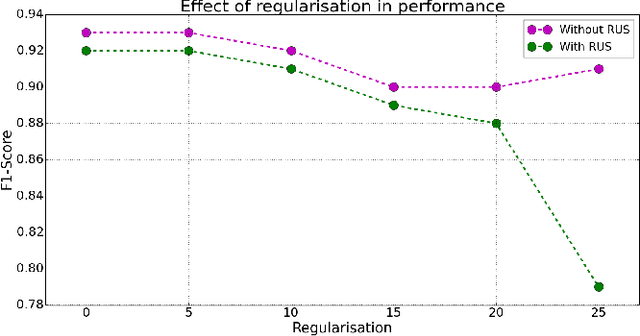
In this paper we consider several algorithms for quantum computer vision using Noisy Intermediate-Scale Quantum (NISQ) devices, and benchmark them for a real problem against their classical counterparts. Specifically, we consider two approaches: a quantum Support Vector Machine (QSVM) on a universal gate-based quantum computer, and QBoost on a quantum annealer. The quantum vision systems are benchmarked for an unbalanced dataset of images where the aim is to detect defects in manufactured car pieces. We see that the quantum algorithms outperform their classical counterparts in several ways, with QBoost allowing for larger problems to be analyzed with present-day quantum annealers. Data preprocessing, including dimensionality reduction and contrast enhancement, is also discussed, as well as hyperparameter tuning in QBoost. To the best of our knowledge, this is the first implementation of quantum computer vision systems for a problem of industrial relevance in a manufacturing production line.